基于波束仿真的合成孔径聚焦成像研究
王海涛,史 振,蒋 俊,梁 斌,甄 理,贾晓媛,殷少华
(1.南京航空航天大学自动化学院,南京 210016;2.南京锅炉压力容器监督检验研究院,南京 210002)
超声波检测作为五大常规无损检测技术之一,由于它的穿透能力强、对人体无害,而且具有被测对象范围广、检测深度大、缺陷定位准确及成本低等诸多优点[1],已广泛应用于工业及高技术产业中,并且成为国内外应用最广泛、使用频度最高且发展较快的一种无损检测技术。超声成像技术是现代超声无损检测技术中一种令人瞩目的新技术,已成为定量检测的重要手段[2-3]。分辨率是衡量超声成像系统优劣的最基本和最重要的指标。近年来人们一直都致力于改善和提高超声成像系统空间分辨率的研究[4],采用的主要措施有:超声数字形成技术、合成孔径成像技术、动态多频率扫描和超声相控阵技术等。
合成孔径成像技术最早出自于军事上的合成孔径雷达技术[5],一般分为机载和星载两种。与直接成像技术相比较,合成孔径成像技术的特点是可以用小孔径的换能器以及低的工作频率来获得比较高的方位分辨率,可以在近场区(即菲涅尔区)工作,在图像的重建过程中,易于应用各种图像处理技术,用于不同成像对象,以提高图像清晰度及信噪比[6]。笔者在合成孔径成像理论的基础上,对合成孔径成像的波束形成进行了仿真研究,从单阵元合成孔径聚焦技术和多阵元合成孔径聚焦技术两个方面分析了参数对波束主瓣宽度和副瓣高度的影响。
1 合成孔径成像基本原理
假设有一小孔径换能器,其水平孔径大小为d。超声换能器按照“扫描-采样-扫描”[7]的方式工作。超声换能器沿水平方向移动扫描,每隔一个恒定的间隔Δx发射并且接收其回波信号,如图1。扫描结束后,对所有点的回波信号进行处理及图像的构建。
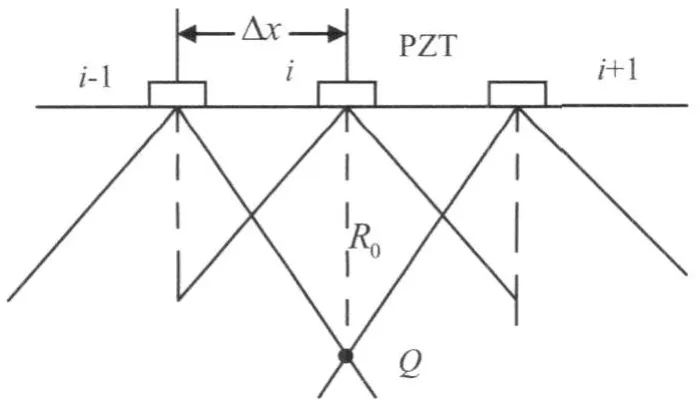
图1 合成孔径聚焦成像原理
在进行图像重构时,根据重建点到各个采样点(换能器阵列单元)的不同距离而造成各个采样点的回波信号有不同的延时τn,即相位发生了变化,对每个采样点的回波信号的相位进行校正后再叠加,即为数据的聚焦过程。在有缺陷的地方,回波信号同相叠加,信号增强;在无缺陷的地方,回波信号是无序随机的,故回波信号较弱。
对于一个小孔径换能器,水平孔径为d,其换能器的半功率点波束角为0.88乘以波长与水平孔径即阵列单元的长度之比[8],因此,对一个均匀照射的合成阵列来说,双程3 dB波束宽度为θ3dB=0.88(λ/d)。如果目标点Q到基元换能器的垂直距离为R0,则基元换能器辐射声束在R0处的合成孔径长度为:
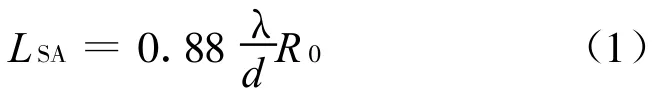
在合成孔径中,各个等效基元是依次顺序发射并接收,因此,各等效基元间的相位差是由发射到接收的“双程”距离差引起的。与实际同样尺寸的直线阵列形成的“单程”指向特性相比,合成孔径各等效基元间的相位差就大了一倍。因此,合成孔径线阵的半功率波束角Bs为:

由式(1)和(2)可得:

对应于合成孔径的方位分辨率为:
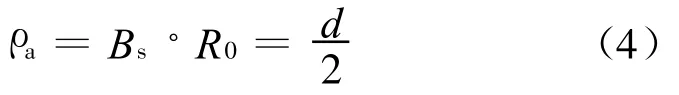
从式(4)可以看出,合成孔径的方位分辨率只与换能器的孔径有关,与目标点的位置和超声波的波长无关。而直接成像系统方位分辨率ρa=0.84(λ/d)R,其中R为目标离换能器的距离[6]。由此可知,要提高超声成像系统的方位分辨率,通常只有两种途径:采用大孔径换能器,或应用高工作频率的换能器,以得到短波长声波。即使如此,方位分辨率还和目标与换能器间的距离有关,离得越远,方位分辨率越差;而且在试件中,随着频率的升高,声波的传播损耗增大,其穿透深度越来越小;而且,大孔径超声换能器也很不方便操作。
由此可见,采用合成孔径技术所带来的好处是用小孔径的实际基元换能器和较低的工作频率,对目标物体进行高方位分辨率的观察,且分辨率不随目标离换能器距离的增大而变差。
2 单阵元合成孔径聚焦
声场在成像场域的分布称为波束形成。波束形成在整个超声成像系统中处于核心的位置,它直接关系到成像的质量。波束的主瓣宽度和副瓣高度理论上是判断波束形成质量的标准。主瓣越窄,成像的侧向分辨率就越高;副瓣越低,成像的伪影就越低,对比度就越明显。
对于单阵元合成孔径,其每次发射和接收只有一个阵元是有效的,即一个阵元发射,同时该阵元进行接收,每个阵元依次发射接收,其工作原理如图2所示。
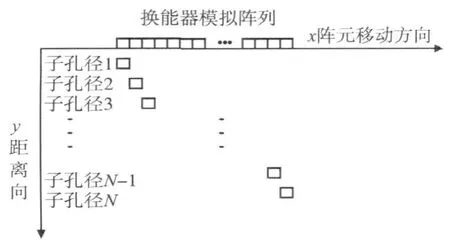
图2 单阵元发射接收模式(共组成N个换能器阵列)
为了方便计算,假设上图的换能器模拟阵列为基元运动后的虚拟线性阵列,换能器初始位置为子孔径1,发射并接收。接着移动到子孔径2位置发射接收,一直移动到子孔径N处。图中的位置只是为了视觉上的便于分析,实际上它是按照水平方向移动的。合成后的虚拟线性阵列,通过对回波信号的处理,可以得到超声波束[9]:
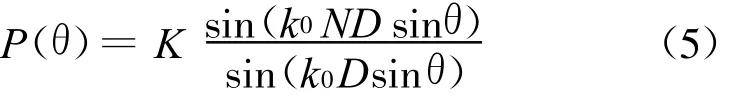
波束仿真参数的设置,由于K是一个固定值,对波束的形成无影响,可以不予考虑,D为阵元移动距离。仿真时假设K=1,阵元总数N=32,中心频率f0=2.0 MHz,超声声速c=1.5 mm/μs,阵元间距分别取λ/2,λ/4和λ/8。不同阵元移动距离下波束如图3所示。
在其他条件不变的情况下,对比D对波束形成的影响,当D=a/2时,发现在±90°处出现了很大的副瓣,这将造成伪影,甚至会对缺陷造成误判。这是由于D间距过大,达到了那奎斯特采样定理的临界值;当D=λ/4时,发现副瓣消失了;当继续减小D时,可以发现,虽然副瓣消失了,但随之而来的主瓣宽度将变得很宽,这使得空间分辨率将减小。因此对于阵元移动间距的选择并不是越小越好。
由合成孔径的方位分辨率ρa=d/2可知,阵元孔径d越小,分辨率应当越高。而事实上得出式(4)时做了菲涅尔近似,如果超声换能器孔径d无限制减小,波束开角过大,菲涅尔近轴条件将被破坏,此时式(4)的结果不再成立。理论分析表明,方位分辨率的极限值是λ/4[10],λ是工作波长,此时可得d=λ/2。仿真时用线性虚拟阵列,忽略了基元的尺寸,移动的距离D非常小,甚至小于阵元的尺寸,这对探头部分的移动装置有很高的要求。
3 多阵元合成孔径聚焦
在合成孔径中,阵元的尺寸较小,其辐射的声功率不大,波束角很宽。因而回波信号较弱。为了提高合成孔径聚焦的信噪比,人们提出了多阵元合成孔径聚焦技术,原理如图4所示。
在这种工作情况下,发射时同时有几个阵元同时发射,然后接收。将这几个阵元移动一段距离,再次发射接收。假设虚拟阵元N,子孔径为L个阵元,子孔径的个数(移动的次数)为K,则K=N-L+1。在这里为了简化计算,假设子阵元的间距和移动距离相同,并且忽略子孔径阵元间发射信号的相互影响。通过计算可得,其合成波束为:
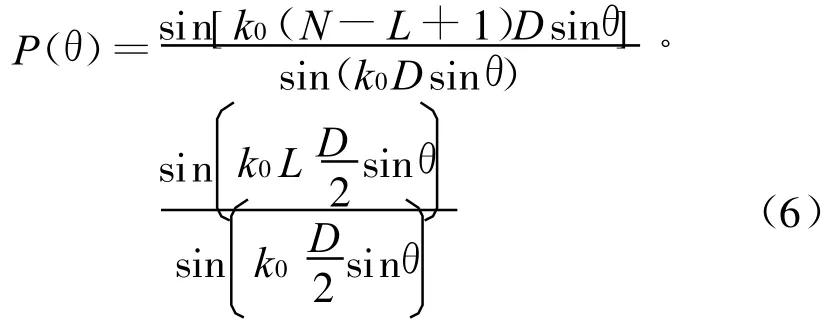
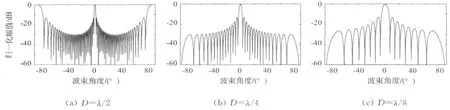
图3 不同阵元移动距离不单阵元孔径的聚集波束
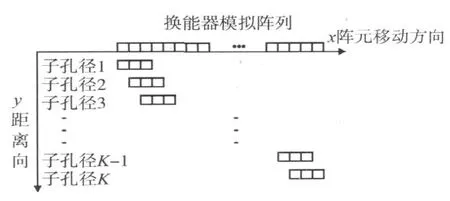
图4 多阵元发射接收模式(共组成N 个换能器阵列)
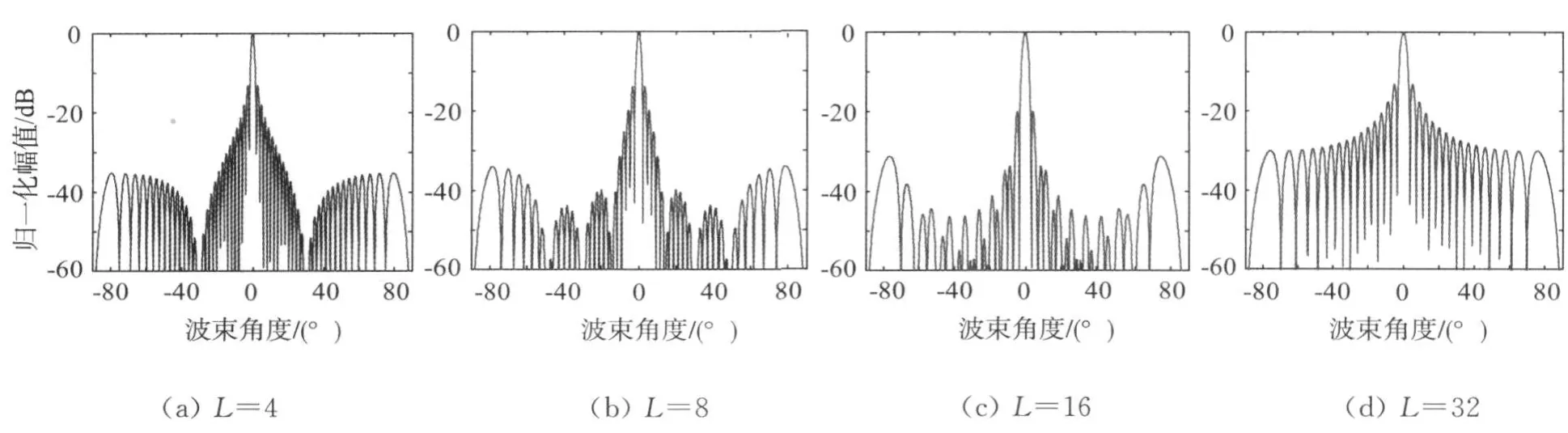
图5 不同子孔径阵元合成孔径聚集波束
为了和单阵元合成孔径聚焦比较,参数设置为:阵元总数N=32,中心频率f0=2.0 MHz,超声声速c=1.5 mm/μs,D=λ/2,L分别取4,8,16和32,不同子孔径阵元数下多阵元合成孔径聚焦波束见图5。
比较图3(a)和5(b)可以发现,多阵元合成孔径聚焦对旁瓣的抑制效果很明显,可使图像对比度提高明显。当子孔径阵元个数小于总的虚拟阵元个数的一半时,波束对旁瓣的抑制效果较好,且主瓣宽度较窄。从公式上也可以看出,当L=32时,此时的多阵元合成波束函数较单阵元合成波束的函数几乎是一样的,因此波束也应该基本相同。这一点从图3(b)和5(d)得到了验证。因此对阵元子孔径的个数选取并不是越多越好,这和系统的总体阵元个数有关。
4 结语
合成孔径成像技术是一种先进的成像技术,在雷达上广泛应用,在超声无损检测方面也有着巨大的应用潜力。介绍了合成孔径成像的基本原理,在此基础上分别从单阵元合成孔径和多阵元合成孔径两个方面做了波束仿真分析。对比可知道,多阵元合成孔径比单阵元合成孔径对旁瓣有较好的抑制效果。
[1]沈建中.超声无损检测的进展[J].无损检测,1998,20(2):31-35.
[2]沈建中.超声成像技术及其在无损检测中的应用[J].无损检测,1994,16(7):202-206.
[3]庞勇,韩焱.超声成像方法综述[J].华北工学院测试技术学报,2001,15(4):280-284.
[4]Bilgutay N M.Enhanced ultrasonic imaging with splitspectrum processing[J].IEEE Trans,1991,37(10):1590-1592.
[5]刘永坦.雷达成像技术[M].哈尔滨:哈尔滨工业大学出版社,1999.
[6]孙宝申,沈建中.合成孔径聚焦声成像(一).应用声学,1993,12(3):43-48.
[7]王邓志,罗斌,罗宏建.合成孔径聚焦超声成像系统研究[J].东北电力技术,2002(12):42-44.
[8]张忠敏,范录宏,皮亦鸣,等.噪声干扰对逆合成孔径雷达成像的影响分析[J].电子对抗技术,2005,20(5):39-42,45.
[9]彭虎.超声成像算法导论[M].合肥:中国科学技术大学出版社,2008.
[10]孙宝申,沈建中.合成孔径聚焦声成像(二)[J].应用声学,1993,12(5):39-45.

