轮轨横向接触系统的自激振动分析

王 振，陈照波，焦映厚，刘旺中

(哈尔滨工业大学 机电工程学院，150001哈尔滨，wangzhen－82@126．com)

轮轨横向接触系统的自激振动分析

王 振，陈照波，焦映厚，刘旺中

(哈尔滨工业大学 机电工程学院，150001哈尔滨，wangzhen－82@126．com)

为了研究轮轨接触过程中发生的自激振动现象对轮轨曲线啸叫噪声的影响，建立了轮轨横向接触系统的单自由度动力学方程，采用基于De Beer模型的改进的新型摩擦系数模型计算了轮轨接触面上的摩擦力变化，用相平面法分析了动、静摩擦系数以及横向蠕滑率对该自激振动系统的稳定性影响．计算结果表明:不稳定的轮轨自激振动会激发车轮的若干模态产生啸叫噪声;轮轨接触系统的结构阻尼大于因摩擦力变化而引起的等效阻尼，轮轨间横向蠕滑率小于0.002 4可以使该系统保持稳定，抑制啸叫噪声．

自激振动;蠕滑率;相平面;轮轨接触

在过弯道时，列车由于自身的动力学特性会在轮轨接触面上产生纵向、横向和自旋蠕滑率．当轨道曲线半径减小时，该蠕滑率数值增大，使得轮轨接触面间的摩擦系数发生变化，进而引起粘滑自激振动，产生轮轨啸叫噪声［1］．由于啸叫噪声的频率特性与车轮受到横向激励而产生的轴向模态相关，以往大多数研究主要是针对轮轨接触区域上横向蠕滑率对啸叫噪声的影响而展开的．Rudd［2］最早于1976年研究了横向摩擦力与蠕滑率之间的关系对啸叫噪声的影响，虽然得到的数据结果后经验证数值偏大，但其采用的研究方法仍是后人研究轮轨啸叫噪声的理论基础．Fingberg［3］之后扩展了Rudd的研究，考虑了车轮的动力学特性、摩擦性能和声辐射特性对啸叫噪声的影响．De Beer等［4］研制了轮轨滚轮接触试验台，通过理论计算和试验验证研究了轮轨横向接触位置对啸叫噪声的影响．国内对于轮轨接触自激振动的研究主要是结合列车运行稳定性，车轮打滑时列车的安全性以及刹车啸叫噪声展开的，而针对曲线啸叫噪声与自激振动间关系的研究比较少［5－7］．因此，研究由于轮轨间横向蠕滑率变化而引起的自激振动现象，有利于发现影响轮轨曲线啸叫噪声的轮轨动力学参数，从而通过对轮轨结构进行修改和处理，达到降低啸叫噪声的目的．

本文对轮轨横向接触过程进行了分析，建立了简化动力学模型，利用在De Beer理论模型基础上改进的新型摩擦系数模型计算轮轨接触面上的摩擦力变化，用相平面法分析了在车轮某一轴向模态下了轮轨接触面间的动、静摩擦系数以及横向蠕滑率对自激振动稳定性的影响．研究结果表明:若该系统最后能收敛到某一稳态点，则系统稳定，不会产生啸叫噪声;若系统不稳定，则最后会出现极限环效应，产生自激振动，引起啸叫噪声．最后分析了增大车轮结构阻尼对抑制啸叫噪声的作用．

1 新型摩擦系数计算模型

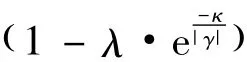
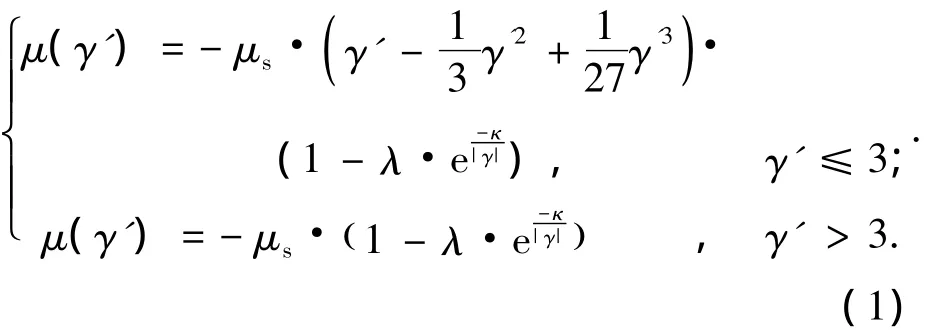
其中，γ'= γGabC22/(μsN)，μs为静摩擦系数，N是接触面上的法向压力，γ为车轮在钢轨上的横向或纵向蠕滑率(蠕滑率 =滑动速度/车轮滚动速度)，a、b为轮轨Hertz接触椭圆斑在纵向和横向的半轴长，G为车轮和钢轨的材料剪切模量，C22为 Kalker系数，C22≈ 2.39+1.36(a/b)－0.025(a/b)2.

图1给出了参数λ和κ的变化对动摩擦系数的影响.

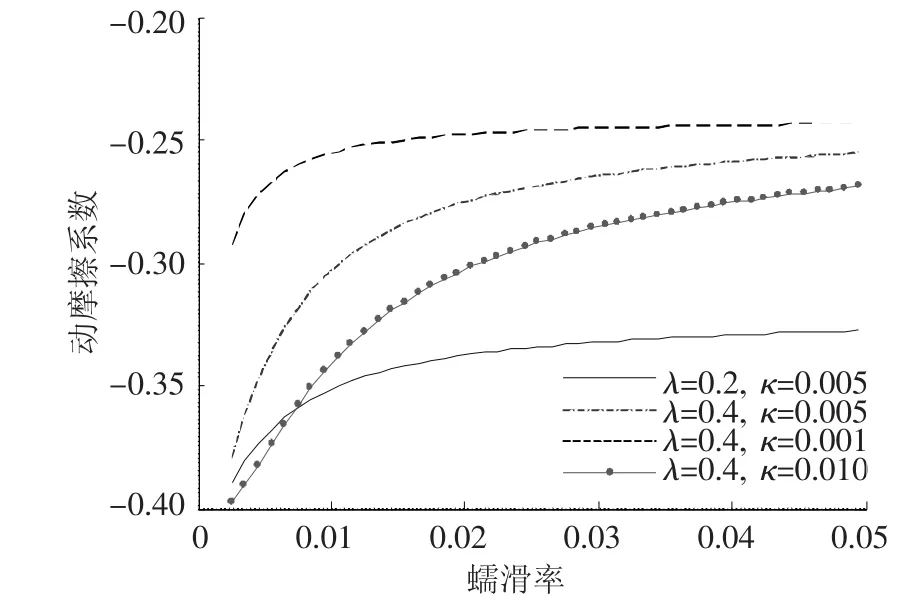
图1 λ和κ的变化对动摩擦系数的影响

下降系数λ用来反映摩擦系数随滑动速度的下降情况，可表示为 λ =(μs－| μk(γ)|)/μs.饱和系数κ用来定义摩擦系数开始下降时的蠕滑率，该参数可以反映接触面的湿度变化对摩擦系数的影响，参数λ和κ都需要通过试验进行设定.从图1中可看出，参数λ增大影响蠕滑率数值较大时的动摩擦系数，参数κ增大影响蠕滑率数值较小时的动摩擦系数.

为验证该新型摩擦系数模型的准确性，在静止摩擦系数μs=0. 4，车轮滚动速度v=10 m/s时，将新型摩擦系数模型与 Kraft，Rudd、De Beer、Poiré-Bochet、Galton模型计算得到的摩擦系数随蠕滑率的变化情况进行了比较［8－9］，如图2所示．其中，De Beer模型中取G为7.9×1010Pa，C22取5. 0，a和b取10 mm 和5 mm，N取42 kN;Poiré-Bochet以及Galton模型中，μs=0.4;新型模型中，λ =0. 4，κ =0.01.

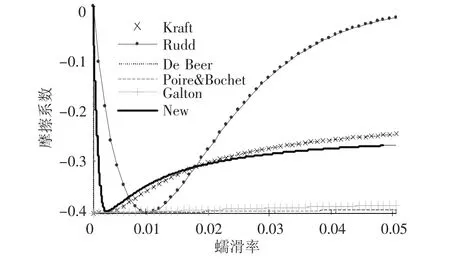
图 2 Kraft、Rudd、De Beer、Poiré-Bochet、Galton 以及新型摩擦系数随蠕滑率的变化曲线

从图2中可以看出，Poiré-Bochet以及Galton模型并不能明显表述摩擦系数随蠕滑率增大而出现的下降现象．Kraft和De Beer模型由于采用了相同的下降函数而在下降阶段相同．Rudd模型中摩擦系数出现下降时的蠕滑率偏大，且摩擦系数数值下降量较大，在蠕滑率为0.05时，摩擦系数接近 0，因此不能较好地描述蠕滑率较大时的摩擦系数变化情况．本文提出的新型模型在蠕滑率较小时的摩擦系数下降曲线比Kraft模型和Rudd模型更为陡峭，且考虑了接触面滑动速度和湿度状况，因此能更好地描述轮轨接触过程中摩擦系数的变化情况．

2 轮轨接触过程自激振动分析

2.1 简化动力学模型的建立

采用皮带－滑块模型来模拟列车过弯道时在轮轨间横向产生的自激振动，建立如图3所示的力学模型．

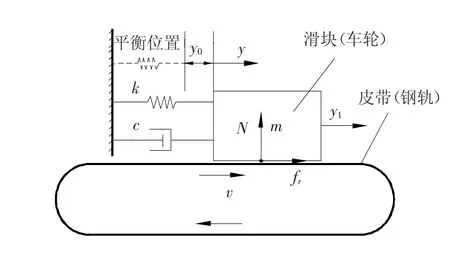
图3 钢轨自激振动简化力学模型

仅对车轮某一阶对啸叫噪声影响较大的振动模态进行分析，用质量－弹簧－阻尼器模型来表示该单模态车轮，用皮带来表示踏面刚性的钢轨(由于仅考虑车轮动力学特性对啸叫噪声的影响，因此将钢轨看作是刚性不变形的)．

设车轮某一振动模态的模态参数为:模态质量m，模态刚度k，模态阻尼c，y1为滑块相对于地面的位移(车轮的横向位移)，v为皮带恒定转速(轮轨间横向平衡滑动速度).

由图3知，滑块与皮带间的相对滑动速度为vr=˙y1－v，其间的滑动摩擦力可表示为fr=N·μ(vr)，其中，N为轮轨间垂向接触力，μ(vr)为随滑块与皮带间相对滑动速度变化的摩擦系数.

当该系统平衡时，滑块位移y1为零，滑块与皮带间平衡相对滑动速度可表示为ve=˙y1－v=－v，此时，平衡滑动摩擦力为

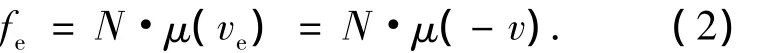
由于此时滑块速度为零，因此只有靠弹簧力来平衡滑动摩擦力，设弹簧伸长量为y0，则有

当有初始扰动位移y作用于滑块使其偏离平衡位置时，滑块的位移为

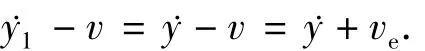
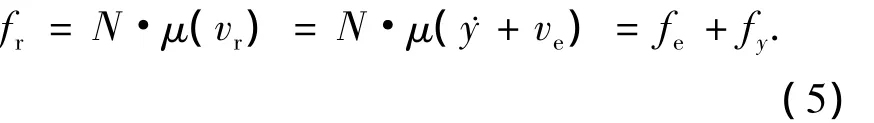
建立该动力学系统运动方程为

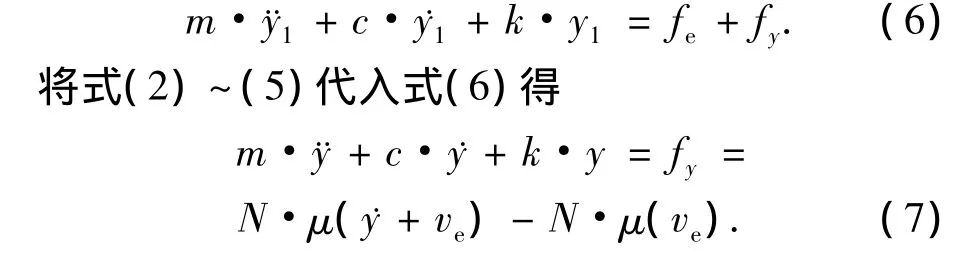
式(7)表明在该皮带 －滑块系统中，由初始扰动位移y产生的摩擦力fy可以激励系统产生自激振动现象.

2.2 自激振动稳定性分析

将摩擦力对滑动速度进行微分后可以得到类似于粘性阻尼性质的参数项，因此对式(7)等号右侧项进行微分处理得到，

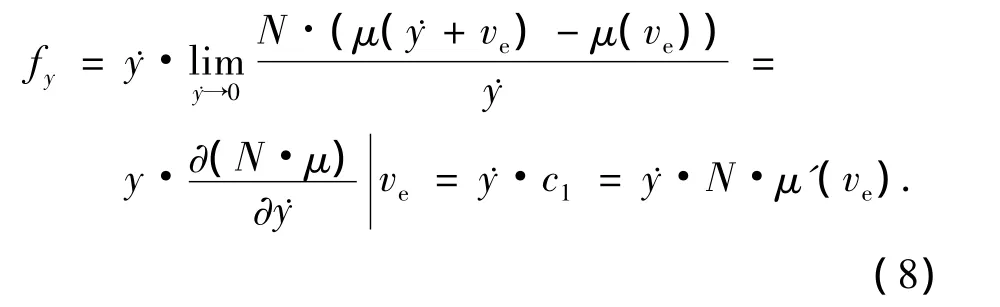
其中，c1即为摩擦力对滑块滑动速度微分处理后的等效阻尼项，代入式(7)有

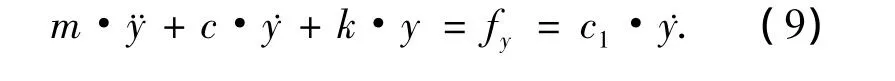
因为摩擦系数对滑动速度的微分在滑块开始滑动前后的符号相反，所以该等效阻尼项可以依据滑动速度的变化对系统产生正或负的阻尼效果．以图2为例，当蠕滑率小于0.002 4时，摩擦系数对滑动速度的微分即摩擦系数曲线的斜率为负，此时c1相当于起到正阻尼作用来耗散系统的能量，减小振动，使系统能收敛到某一平衡点;当蠕滑率大于0.002 4时，摩擦系数曲线斜率为正，此时c1相当于起到负阻尼作用来增加系统的能量，增大振动，使系统变得不稳定，出现自激振动现象.

通过以上分析可知，若要整个皮带 －滑块系统达到平衡状态，需使系统的总阻尼为正，以达到耗散系统能量的目的.把式(9)变换为

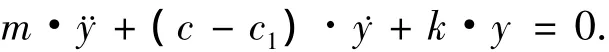
若要使系统总阻尼为正，则要c－c1＞ 0，又因为系统结构阻尼项c恒大于零，所以需根据由摩擦力带来的等效阻尼项的正负情况来调节系统结构阻尼以使c－c1＞0.当c1为负值时，c－c1相当于正阻尼，此时c取任意值都会使系统稳定;当c1为正值时，c－c1相当于负阻尼，c＞c1时才能使系统稳定.

为便于研究轮轨横向蠕滑率对自激振动的影响，将式(8)变换为摩擦力对轮轨横向蠕滑率的微分，得到

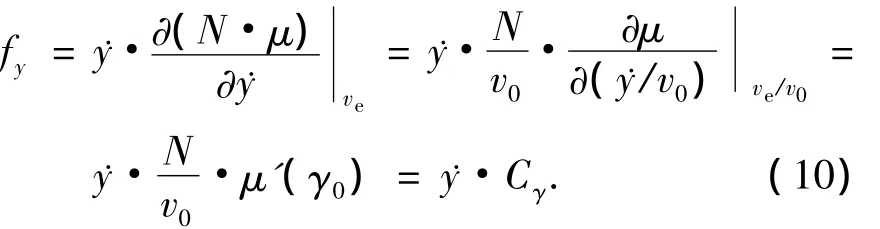
其中，v0为车轮滚动速度，γ0为轮轨稳态横向蠕滑率(即为轮对在轨道上横向受力平衡时的蠕滑率，用来确定自激振动系统的稳态点)，Cγ为摩擦力对稳态横向蠕滑率微分处理后的等效阻尼项.

利用本文提出的新型摩擦系数模型对等效阻尼Cγ与振动系统稳定性的关系进行分析．在新型摩擦系数公式中选取［10］:车轮剪切模量 G为7.9 ×1010Pa，Kalker系数C22为5. 0，轮轨Hertz接触椭圆斑在纵向和横向的半轴长a和b为10 mm和5 mm，轮轨垂向接触力N为40 kN，车轮滚动速度v0为10 m/s，下降系数λ为0. 4，饱和系数κ为0.01．在［－0. 05，0.05］的蠕滑率区间上得到摩擦系数曲线如图4所示．

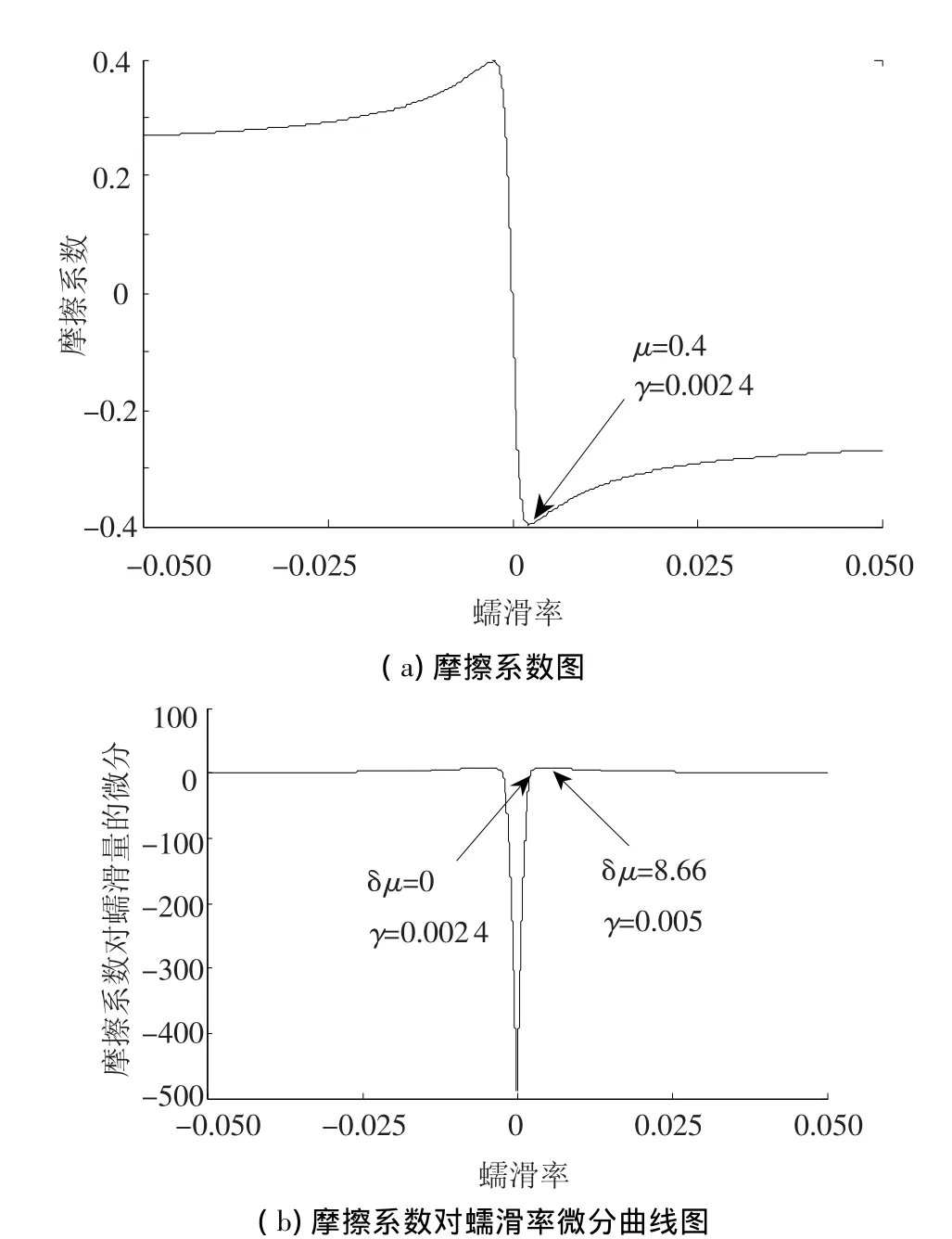
图4 基于新型摩擦系数模型得到的摩擦系数和摩擦系数对蠕滑率微分曲线

从图4中可看出，由于等效阻尼Cγ的正负与摩擦系数对蠕滑率微分有关，因此在蠕滑率γ≤0.002 4时，Cγ为负，此时系统恒为稳定状态;γ＞0.002 4时，Cγ为正，这时需要系统结构阻尼C＞Cγ才能使系统稳定，而当γ=γp=0.005时dμ最大为 8. 66，由式(10)得，需要 C ＞Cγp=34 640 N·s/m．因此若要使系统稳定，有两种解决办法:(1)调节系统结构阻尼，使C＞Cγp;(2)减小轮轨间横向蠕滑率，使γ≤0.002 4.

如果考虑用系统阻尼比来衡量系统稳定性，若阻尼比能满足

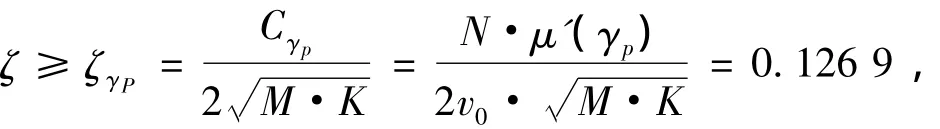
则系统可达到稳定状态.

2.3 针对车轮具体参数的计算

本文建立的单自由度振动模型需选择车轮某一阶对啸叫噪声影响较大的振动模态的模态参数进行计算分析．通过对本实验室车轮模型进行模态分析后，选取426.3 Hz对应的模态，其径向剖面振型如图5所示．

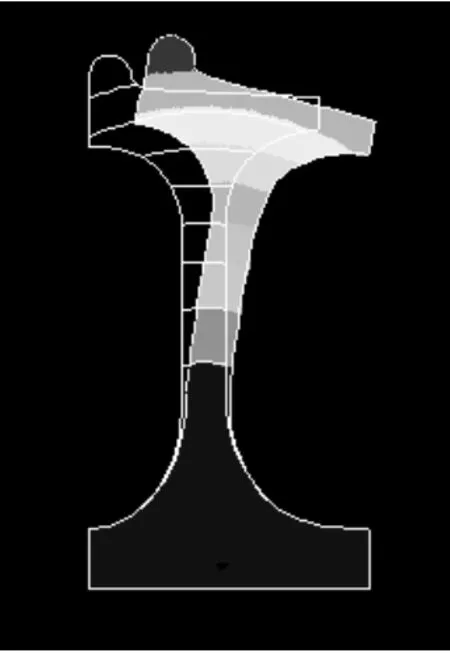
图5 车轮模态振型径向剖面图

在该模态下车轮轮缘的轴向振动比较明显，这对车轮与钢轨间的横向振动贡献较大，因此选取该阶模态具有代表性．经过模态参数识别处理后，得到:模态质量 m为320 kg，模态刚度 k为5.82×107N/m，模态阻尼c为2 729.4 N·s/m，阻尼比ξ为0.01．由于在式(10)中，等效阻尼Cγ与轮轨稳态横向蠕滑率γ0有关，因此需根据γ0值的大小来分析该系统的稳定性.

(1)当 γ0≤0.002 4 时，取γ0=0.001 8，y0= 0，初始蠕滑率分别为0.001 5和0.002 0，车轮横向初始位移都为1×10－6m，此时该系统的相平面图和速度－时间曲线如图6、7所示.当γ0≤0.0024时，系统恒为稳定状态，最终都收敛到稳定点y0= 0，γ0=0.001 8，速度在经过0.02 s后达到稳定，并且速度收敛的时间与初始蠕滑率和横向位移无关.

在图4所示的摩擦系数对蠕滑率微分曲线中，当γ0≤0.002 4时，随着蠕滑率的减小，摩擦系数对蠕滑率的微分增大，使Cγ也相应增大，这就相当于增大了系统的结构阻尼，从而使速度达到平衡所需的时间也相应减少，所以在系统恒为稳定的状态时，若要使系统尽快收敛，可以减小轮轨横向平衡蠕滑率．

2)当 γ ＞ 0.002 4时，取 γ0=0.006 0，y0=0.令Y=y'，导出相轨迹的一阶微分方程为

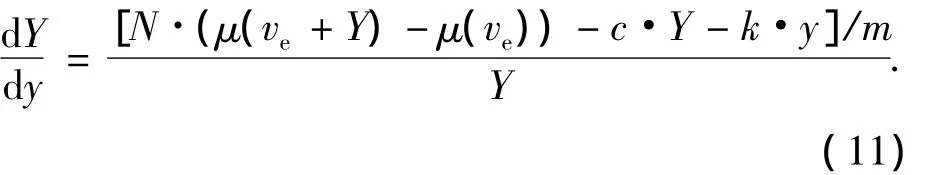
以任意常数α为等倾线斜率，由式(11)导出等倾线族的方程为

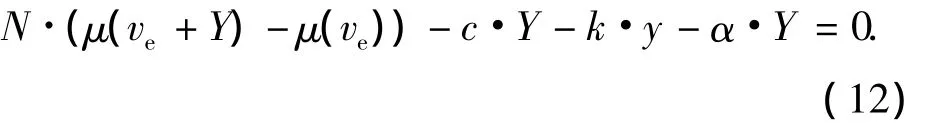
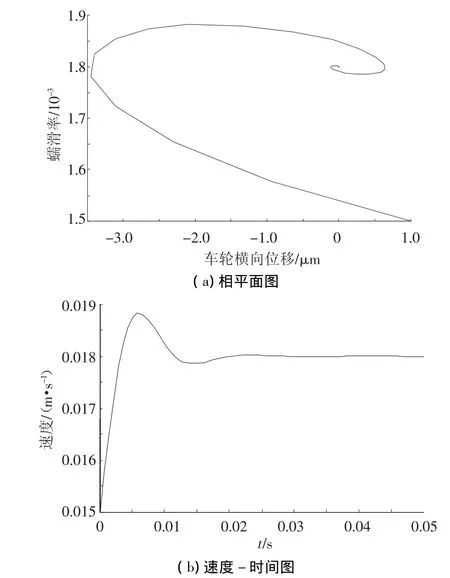
图6 γ0=0.001 8，y0= 0，初始蠕滑率为0.001 5，车轮横向初始位移为1×10－6m时的相平面图和速度－时间图

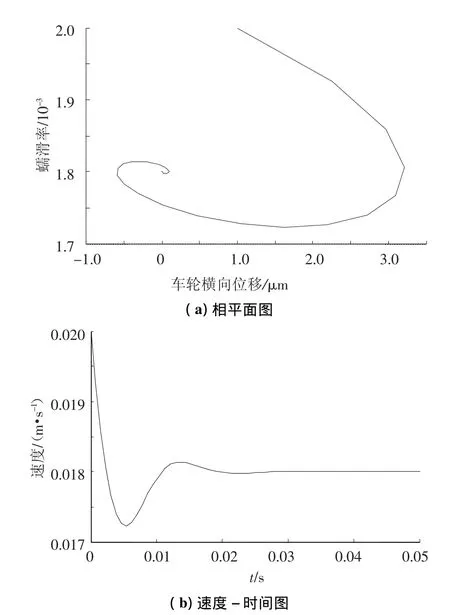
图7 γ0=0.001 8，y0= 0，初始蠕滑率为0.002 0，车轮横向初始位移为1×10－6m时的相平面图和速度－时间图

利用Liénard作图法绘制该系统的相平面图［11］．首先做出零斜率等倾线(图8)，其中 A点为极限环在等倾线上的出发点，B点为极限环和相轨迹的围绕点．

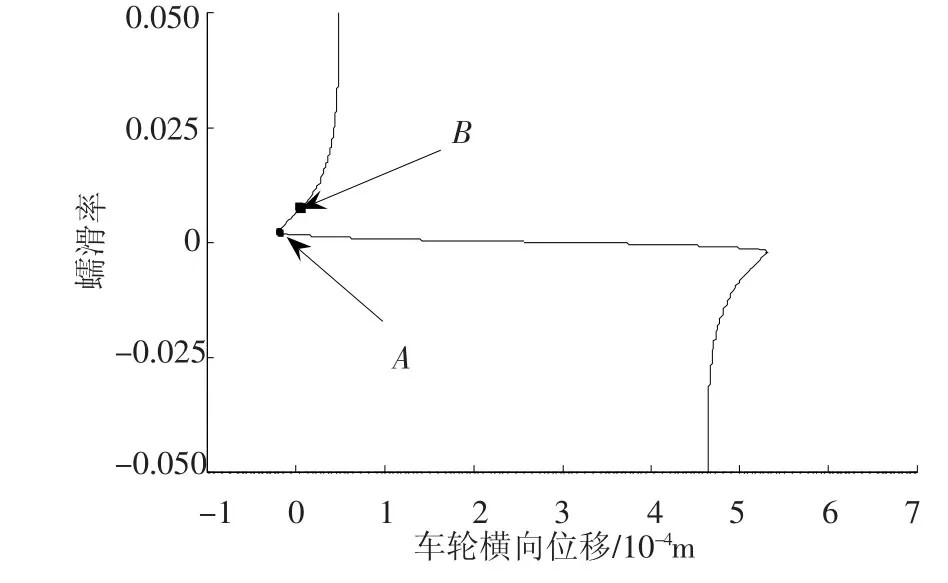
图8 系统零斜率等倾线图

在初始蠕滑率分别为 0. 006，0. 008，0. 015，车轮横向初始位移分别为 0.5×10－4、2×10－4、1×10－5m时，系统的相平面如图9所示．

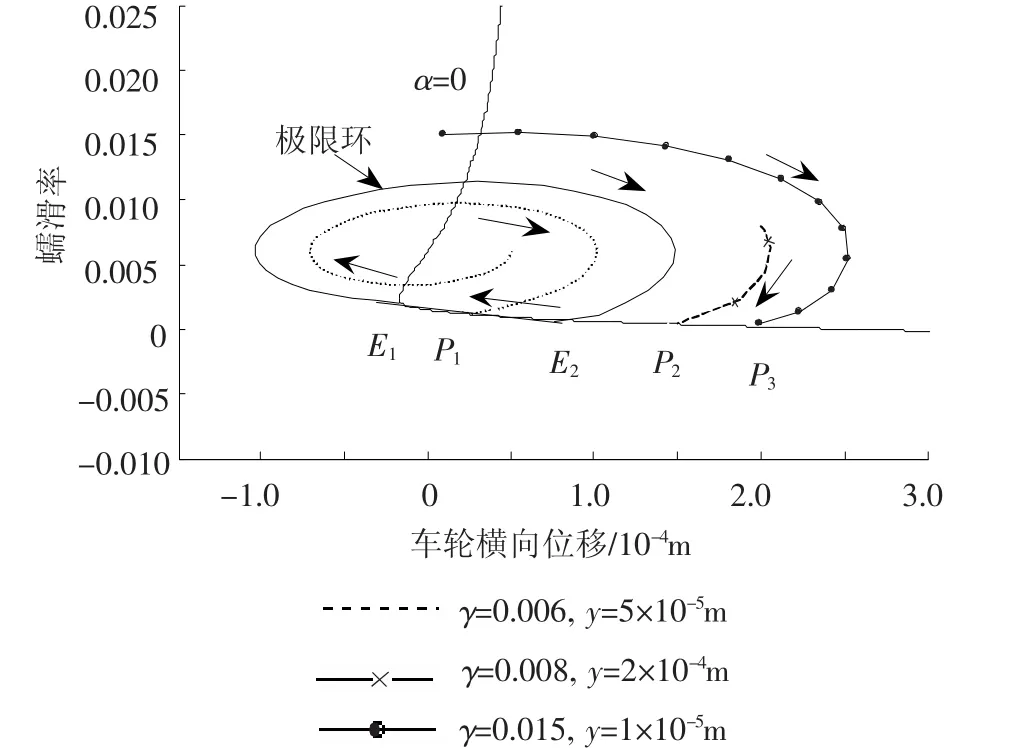
图9 γ0=0. 006，y0=0时系统的相平面图

从图9中可以看出，由于系统结构阻尼c=2 729.4 N·s/m ＜ Cγp=34 640 N·s/m，因此在3种初始状态下，相轨迹在经过零斜率等倾线时(交点为 P1，P2，P3)，将会沿水平方向运动，此后一直运动到E1点(即为图8中的A点).在这个阶段，车轮相对于钢轨以很小的蠕滑率进行蠕动，轮轨间近似于静止状态，系统通过变化着的静摩擦力做功来存储能量.当运动到E1点后，静摩擦力平衡不了弹簧力和粘性阻尼力，系统能量被释放，相应从E1点出发沿着极限环运动到E2点，形成封闭相轨迹，使系统发生自激振动现象.

在该γ0值条件下，增大系统的结构阻尼，使c=40 000 N·s/m ＞Cγp，此时系统阻尼比ζ=0.146 6，选取初始条件为:γ =8 ×10－3，y=2 ×10－4m，得到系统的相平面和速度 －时间曲线如图10所示.

在图10中，系统的相轨迹最终收敛到以稳定点为中心的极限环，且该极限环的尺寸为:蠕滑力方向，Δ ＜2×10－4，横向位移方向，Δ ＜4×10－6m．在速度——时间图中可以看出速度在经过0.5 s后达到稳定收敛，因此证实了增大系统阻尼可以使轮轨接触达到稳定状态．

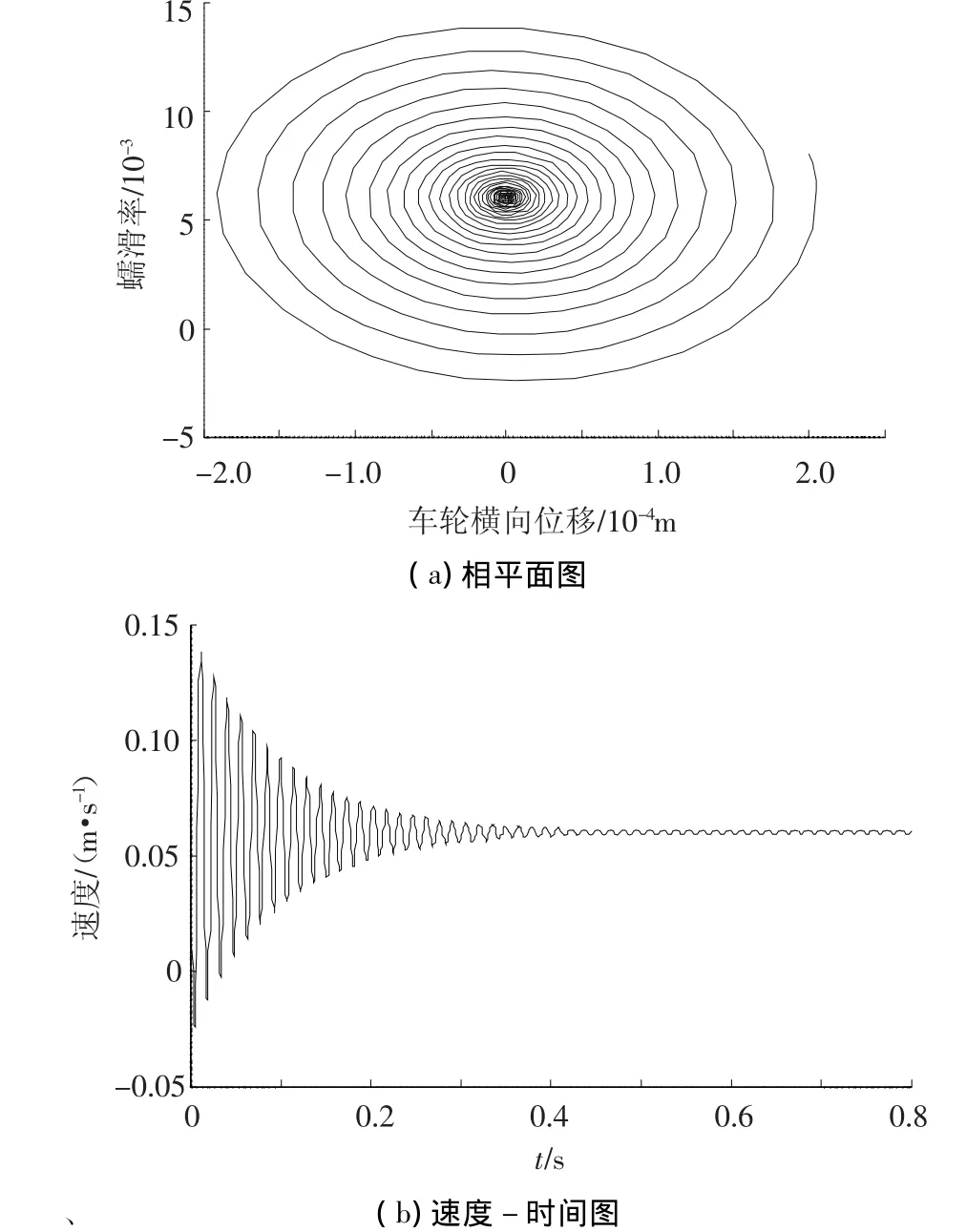
图10 系统结构阻尼C=40 000 N·s/m＞Cγp，初始条件为:γ=8×10－3，y=2×10－4m 时的相平面图和速度－时间曲线图

3 结论

1)将车轮与钢轨的横向接触过程简化为滑块与皮带的接触，建立了动力学系统运动方程，结合具体车轮参数，用相平面法分析了该系统的稳定性．

2)通过调节系统结构阻尼使C ＞Cγp，或减小轮轨间横向蠕滑率使γ≤0. 0024，可使系统达到稳定状态，在相平面中相应为相轨迹收敛到一稳定点或稳定极限环．

3)若系统不稳定，相轨迹形成的极限环的尺寸会使轮轨横向接触产生自激现象．

［1］ IWNICKI S．Handbook of railway vehicle dynamics［M］．New York:Taylor＆ Francis Group，2006:301－304．

［2］ RUDD M J．Wheel/rail noise-Part II:wheel squeal［J］．Journal of Sound and Vibration， 1976，46(3):381－394．

［3］ FINGBERG U．A model of wheel-rail squealing noise［J］．Journal of Sound and Vibration， 1990，143(3):365－377．

［4］DE BEER F G，JANSSENS M H A，KOOIJMAN P P C［J］．Journal of Sound and Vibration， 2003，267(3):497－507．

［5］姚远，张红军，罗赟，等．机车打滑时轮对纵向振动研究［J］．机械工程学报， 2009，45(7):199－203．

［6］朴明伟，樊令举，梁树林，等．基于轮轨匹配的车辆横向稳定性分析［J］．机械工程学报， 2008，44(3):22－28．

［7］李博，丁千，陈艳．刹车系统摩擦自激振动的数值研究［J］．科技导报， 2007，25(23):28－32．

［8］MONK-STEEL A D，THOMPSON D J，DE BEER F G，et al.An investigation into the influence of longitudinal creepage on railway squeal noise due to lateral creepage［J］．Journal of Sound and Vibration， 2006，293(3 －5):766－776．

［9］PERIARD F．Wheel-rail noise generation:curve squealing by trams［D］．Delft:Delft University of Technology，1998:151－153．

［10］丁文镜．自激振动［M］．北京:清华大学出版社，2009:99－112．

［11］MAKOTO I，TAKUMI B，HIROAKI I，et al.Effect of moderating friction of wheel/rail interface on vehicle/track dynamic behavior［J］．Wear， 2008，265(9/10):1497－1503．

Self-excited vibration analysis for wheel/rail lateral contact system

WANG Zhen，CHEN Zhao-bo，JIAO Ying-hou，LIU Wang-zhong

(School of Mechatronics Engineering，Harbin Institute of Technology，150001 Harbin，China，wangzhen－82@126．com)

To study the influence of self-excited vibration on the curve squeal noise in the wheel/rail contact，the dynamical equation for 1-DOF wheel/rail lateral contact system is derived．A new friction coefficient model based on De Beer model is adopted to calculate the friction force in the wheel/rail contact surface．The influence of kinetic and static friction coefficients as well as the lateral creepage on the stability of self-excited vibration system is investigated．The calculation results show that wheel’s inherent modes will be excited by the unstable self-excited vibration．If the structural damping of wheel/rail contact system is larger than the equivalent damping of the friction force，or the value of lateral creepage is less than 0. 0024，the self-excited vibration system will be stable，and thus the curve squeal noise can be restrained．

self-excited vibration;creepage;phase plane;wheel/rail contact

TB533

A

0367－6234(2011)09－0056－06

2010－07－12．

科技部科技人员服务企业行动项目(2009GJB20012)．

王 振(1982—)，男，博士研究生;

陈照波(1967—)，男，教授，博士生导师;

焦映厚(1962—)，男，教授，博士生导师．

(编辑 杨 波)