孔板送风房间内污染物分布的模拟与实验
孙丽颖,魏慧娇
(1.哈尔滨工程大学 航天与建筑工程学院,150001哈尔滨,sunliying@hrbeu.edu.cn;2.中国建筑科学研究院天津分院,300834天津)
孔板送风房间内污染物分布的模拟与实验
孙丽颖1,魏慧娇2
(1.哈尔滨工程大学 航天与建筑工程学院,150001哈尔滨,sunliying@hrbeu.edu.cn;2.中国建筑科学研究院天津分院,300834天津)
为研究孔板送风条件下室内污染物体积分数的分布规律,采用实验测试和数值模拟两种方法.建模时采用基本模型和N点风口模型两种方法进行孔板入口边界条件的处理,模拟结果表明:两种处理方法计算的污染物体积分数分布规律相近;将实验数据和模拟结果进行对比,其变化趋势吻合良好,其中N点风口模型的模拟结果更接近实验情况,从而验证了应用该模型研究室内污染物分布特性的可行性.
孔板送风;污染物;数值模拟
随着经济发展,人们对室内装修的要求不断提高,各种新型材料在室内装饰装修中的广泛采用,导致室内空气品质开始恶化,已经严重威胁到室内人员的身心健康.因此,解决室内空气污染问题日益受到人们的关注.空调系统的送风对室内污染物可以起到去除或稀释的作用,在送风过程中,污染物体积分数的变化规律与分布情况可以通过实验与数值模拟的方法来研究.随着计算流体力学技术的广泛应用,室内空气品质的研究借助于数值模拟方法,取得了很多成绩,李丽等[1]用数值模拟方法研究了新风量对室内Total Votatile Organic Compound(简称TVOC)体积分数的影响.张明远[2]运用数值计算的方法,分析比较了不同送回风方式对室内污染物体积分数分布的影响.赵彬等[3]采用三维CFD程序STACH-3对洁净室的速度场进行了数值模拟,得出的结论是用“N点风口动量模型”描述孔板风口可以得到与实际相符合的模拟结果.张文胜等[4]对一个体积为0.45×0.45×0.4(m3)的密闭小室,在送风温度恒定的条件下对小室内孔板送风气流分布情况进行了实验研究.李勇[5]利用CFD软件,对各种通风空调方案下ICU病房内温度场、速度场、体积分数场的数值模拟结果进行分析比较,得出结论:百叶送风时病房的排污能力要优于孔板送风.目前,国内外通过数值模拟分析室内气流组织的研究较多,对孔板送风条件下室TVOC体积分数场的CFD模拟分析与实验验证相对较少,存在的问题是数值模拟的方法、边界条件和初始条件设定的合理性未能很好地用实验来验证,使得模拟结果的可信度降低.本文以某一采用孔板送风的实验房间为研究对象,通过实验测试和数值模拟的方法,研究孔板送风过程中实验房间内污染物TVOC体积分数的分布规律,在进行孔板送风口的边界条件处理时,采用两种不同形式的简化,并将实验与2种模拟结果进行比较,从而验证所建模型的正确性.
1 数值模拟基础及模型建立
1.1 计算基础
以哈尔滨工程大学人工环境实验室的空调房间作为研究对象,房间的物理模型见图1.房间尺寸为5m×3.5 m×2.8 m,一门一窗位于南墙上.设实验房间内共有2张桌子和2个人,根据实际情况设2张桌子是污染物TVOC的主要散发源.室内温度为18℃,送风方式为孔板送风,并且整个顶棚布满孔板.回风口为百叶风口,尺寸为0.65 m×0.42 m,位于房间的西墙下方,桌子尺寸为0.7 m×0.4 m×0.6 m.

图1 房间的物理模型
1.2 数学模型
大量实验表明空调房间内的气流基本上是湍流,本文采用目前应用最广、接受检验最多、数值技术也最成熟的湍流模型——k-ε二方程模型[6].采用k-ε二方程模型求解湍流对流换热问题时,k-ε方程与动量方程、能量方程、连续性方程一起构成了室内空气流动的控制方程,其通用形式[7]为

式中:φ为通用变量,分别表示动量方程中的速度u,能量方程中的温度T,体积分数方程中的C,湍流动能方程中的湍流动能K及湍流动能耗散方程中的耗散率ε;Γφ为广义扩散系数;Sφ表示广义源项.
划分网格时在x、y、z方向上网格的长度≤0.11 m,并在人体、桌子、风口附近进行加密,共生成143 851网格.然后采用控制容积法将控制方程在网格上离散,差分格式使用混合格式,求解算法为SIMPLE算法.
1.3 边界条件和初始条件
在进行数值计算时,计算所需的边界条件和初始条件如下:
1)精确的CFD模型可对室内污染物体积分数的分布进行全面预测,风口模型的设定是影响计算精度的主要因素之一.孔板送风口的边界条件简化采用以下两种处理方法:模型一采用“N点风口模型”[3],即利用外形面积与原孔板风口相等的简单开口替换复杂孔板风口,以描述其入流边界条件,并保证入流的质量流量和动量流量与实际一致;模型二将孔板风口等效为一个简单开口,其面积与孔板风口的有效通过面积相等,这样可确保入流的动量流量和质量流量与实际一致[8].
2)在满足工作区温湿度和风速要求的基础上,房间送风量可取 750 m3/h,送风温度为18℃.
3)因为实验室建在室内,可忽略实验室围护结构内外的传热问题,模型中设定墙体为没有厚度的绝热墙体.
4)室内空气中TVOC的初始体积分数为620×10-9.认为室内空气为干空气,室内空气初始温度18℃.由于桌子散发污染物速率很小,短时间内对室内环境的影响较小,所以近似认为桌子散发污染物速率为0.
2 实验方法与步骤
为得出实际情况下室内污染物体积分数分布规律,对实验房间内的污染物分布进行了测试.实验在图1所示的房间中距地面1.0 m处布置测点5个,其位置如图2所示.图2中将人和桌子简化成长方体,圆圈代表测试点.实验前在实验室内人为布置污染源,污染源采用建筑装修中常用的粘合剂涂在桌面上,则室内的两张桌子成为污染物TVOC的主要散发源.为了使室内污染物的体积分数符合实际新装修建筑室内的一般水平,将污染源在室外放置约1 h,再放置室内约6 h,以使其污染物充分散发并均匀分布在室内.污染物释放过程中,实验室的门窗全部关闭,以防止人为的扰动.室内总挥发性有机物(TVOC)的体积分数用PpbRAE VOC检测仪(PGM-7240X型)检测,该设备的测试范围是 0~9 999×10-9,精度为10%.
主要实验步骤:
1)按照仪器的使用要求连接仪器,并进行使用前的校准工作.
2)在各测点测试TVOC的初始体积分数,测试时尽量减少室内人员走动,以防止气流扰动对实验造成的误差.
3)打开空调系统,设置送风温度为18℃,送风相对湿度为36%,风量设置为750 m3/h.开始送风时监测测点处的污染物体积分数,当体积分数发生变化时开始测量各测点的污染物体积分数,本实验取各测点5 s内的污染物体积分数的平均值作为实验结果.每组测试时间间隔为60 s,共计测试10~15组.
4)当室内污染物体积分数随时间的变化不大时,停止测量,关闭实验仪器,关闭空调系统.

图2 测试点布置(m)
3 模拟结果分析
3.1 两种模型不同时刻模拟结果比较
图3为不同时刻两种模型模拟结果比较,可以看出:
1)采用两种不同模型的模拟结果,室内污染物体积分数分布规律相近,其中测点1和测点4由于距离污染源较近体积分数较高.采用模型一时同一时刻室内测点2的体积分数最低,而采用模型二时测点3的体积分数最低,其主要原因是模型二相对于模型一送风口尺寸减小了,使得模型2中的测点3刚好位于送风口的正下方,而测点2位于送风口的边缘处.
2)同一时刻模型二所得室内污染物体积分数较低,主要是因为模型二送风口较小,风速相对较大.模型二中测点4所处的位置位于体积分数“死角”内,所以体积分数偏高.
3)送风1 000 s时,室内污染物体积分数变化趋于稳定,两种模型模拟得到的室内污染物体积分数基本相同,各测点TVOC体积分数相差1 ~2 ×10-9.
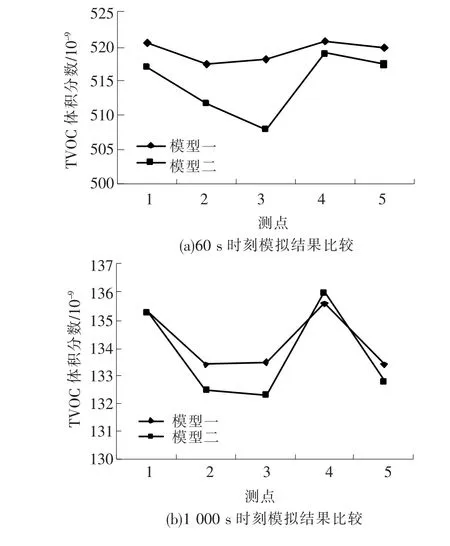
图3 两种模型不同时刻模拟结果对比
3.2 各测点污染物体积分数逐时变化情况
图4是采用两种模型时测点1和测点3污染物体积分数逐时变化曲线,两曲线基本重合,体积分数下降趋势完全相同,在大约第900 s时体积分数变化曲线的斜率很小,室内TVOC体积分数已趋于稳定.
3.3 Y方向污染物体积分数分布
孔板送风所形成的室内气流组织形式是典型的“活塞流”,送风从上部空间逐渐向下推进,所以同一时刻距地面不同高度的测点上污染物体积分数有较大差别,本文取房间内测点3位置上距地面不同高度上的5个测点,分析同一时刻各测点的体积分数值.
从图5可以看出:
1)两种模型的模拟结果均表明,在送风初期,离地面距离越大,测点污染物体积分数越低.采用模型二得出的各测点体积分数随高度变化较大,60 s时刻模型一最大与最小体积分数值相差20×10-9,模型二最大与最小体积分数值相差45×10-9.
2)随着送风时间的延长各测点的体积分数差值逐渐减小,说明室内污染物体积分数逐渐趋于均匀状态.
3)距地面较近的测点污染物体积分数随高度的变化并不大,而在距地面1.4 m以上的区域内高度会对污染物体积分数产生很大影响,模型二表现得更加明显.这说明射流区污染物体积分数变化较明显,在工作区污染物体积分数较均匀.

图4 测点1和测点3体积分数变化曲线

图5 y方向体积分数分布对比
3.4 速度场比较
图6是采用两种不同模型模拟时,室内(z=0.5 m截面与x=0.25 m截面)的流线分布情况.
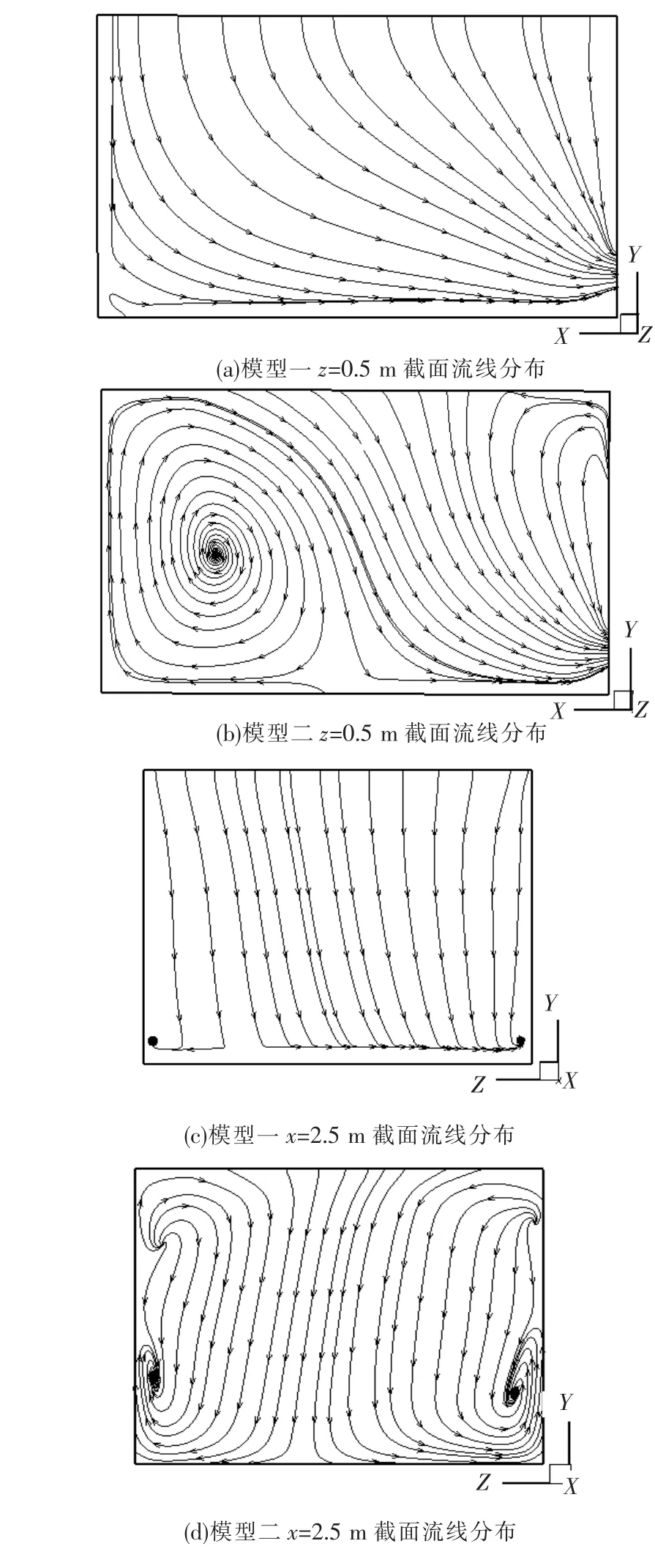
图6 两种模型模拟的流线分布
采用不同简化模型进行数值模拟时,室内气流分布有很大的不同.采用模型一时室内气流分布均匀,送风口下的区域内流线近似平行,较为符合实际情况下的气流分布;采用模型二时,在出风口下的区域内流线近似平行,而在出风口的两侧气流分布出现漩涡,其中z=0.5 m截面左侧气流因为受到人的阻挡而出现一个很大的漩涡.正是由于两种模型模拟的室内气流分布的差异导致室内污染物的体积分数分布有所不同.
4 数值模拟的验证
数值模拟结果表明,采用两种不同的简化模型进行模拟的结果相差不大,但是哪种模型的模拟结果更接近实际情况,还需通过实验检验.
图7是将不同时刻的模拟值和实验值绘制在同一坐标系下的体积分数分布曲线.

图7 模拟值和实验值对比
通过图7中模拟值与实验值的对比,可得出下述结论:
1)模拟结果与实验结果显示的室内空气中污染物体积分数分布规律符合较好,对于不同测点,两者在数值上存在0.1% ~15%的误差,测点1与测点4由于靠近污染源,TVOC体积分数比较高,测点2与测点5体积分数较低,而测点3处于平均水平.
2)第1 000 s时,室内TVOC体积分数基本达到稳定,实验所测得的平均值(142×10-9)与模拟结果(137×10-9)有一定差别,但误差较小,进一步证实了用数值模拟的方法研究室内污染物分布特性的可行性.
3)实验测得数据与采用模型一所得的计算结果更为接近,因为在实际情况中送风小孔均匀布满整个天花板,“N点风口模型”利用外形面积与原孔板风口相等的简单开口替换复杂孔板风口,更符合实际情况,更适合进行孔板送风条件下污染物分布的数值研究.
5 结论
1)孔板送风对室内污染物有明显稀释作用.对于本文研究的空调房间,送风量为750 m3/h时,房间开始送风120 s后人坐姿呼吸层上的污染物体积分数已经降到了国家规定值500×10-9之下,送风900 s后,污染物体积分数趋于稳定.
2)模拟和实验结果表明,室内污染物体积分数分布和送回风口、污染源的位置有很大关系,距离送风口较近的区域内污染物体积分数较低,污染源及其周边的污染物体积分数较高.
3)孔板送风采用两种入流边界条件处理方法的模拟结果均和实验结果吻合较好,模型一的模拟结果更接近实验情况,因此建议采用模型一的“N点风口模型”进行孔板送风条件下污染物分布的数值研究.
[1]李丽,徐文华.新风量对室内VOCs浓度分布影响的模拟分析[J].洁净与空调技术,2003(3):16-20.
[2]张明远.室内高大空间污染物分布数值模拟[D].北京:华北电力大学,2003.
[3]赵彬,曹莉,李先庭.洁净室孔板型风口入流边界条件的处理方法[J].清华大学学报:自然科学版, 2003,43(5):690 -692.
[4]张文胜,安大伟,董瑞,等.密闭恒温小室流场均匀性的研究[J].山东建筑大学学报, 2006,21(5):430-433.
[5]李勇.ICU病房空调通风系统数值模拟[D].武汉:华中科技大学,2006.
[6]鹿世化,黄虎,李奇贺.数值模拟用于室内空气质量控制的研究进展[J].暖通空调, 2007,37(5):40 -46.
[7]陶文铨.数值传热学[M].2版.西安:西安交通大学出版社,2001.
[8]NIELSEN P V.Description of supply openings in numerical models for room air distribution [J].ASHRAE Transactions, 1992,98(1):963 -971.
Numerical simulation and experimental investigation of contamination distribution in a chamber with perforated ceiling air supply
SUN Li-ying1,WEI Hui-jiao2
(1.College of Aerospace and Civil Engineering,Harbin Engineering University,150001 Harbin,China,sunliying@hrbeu.edu.cn;2.China Academy of Building Research(Tianjin Branch),300834 Tianjin,China)
To study the contamination distribution in a chamber with perforated ceiling air supply,simulative analysis and experimental tests are carried out in this paper.In modeling,the Basic model and N-spot air model are both used for defining the orifice entrance boundary condition.The simulation results show that the distribution of contamination concentration agrees well with the test result.Especially,the simulation result of the N-spot air model is closer to the experimental one,which proves the feasibility of this model in analyzing indoor contamination distribution.
perforated ceiling air supply;contamination;numerical simulation
TU831.3
A
0367-6234(2011)08-0135-05
2010-03-10.
中央高校基本科研业务费专项资金资助项目(HEUCF100206).
孙丽颖(1973—),女,博士,副教授.
(编辑 赵丽莹)

