格网点电离层垂直改正误差分析及其改进算法研究①

范媚君，周建华，王梦丽

（1.北京环球信息应用开发中心，北京100094；2.解放军信息工程大学测绘学院，河南 郑州450002）

0 引 言

广域差分完好性信息通常包括用户差分伪距误差（UDRE）和网格点电离层垂直改正误差（GIVE）［1－3]，计算方法都是在一定置信度下的误差估计，即误差的置信限。伪距误差由观测值与理论值作差获得，可直接计算置信限，而格网点电离层延迟误差需对观测值进行插值及拟合处理，不能直接计算置信限，只能给出该置信限的约束值，相当于一个“包络”。提出了一种格网点电离层垂直改正误差算法，该算法在保证一定完好性风险的条件下缩小了误差估计值，使其更加接近真实值，从而提高了系统可用性。

1 格网法电离层延迟改正法

对于电离层延迟采用双频技术可以有效地校正电离层延迟，而单频接收机只能用电离层模型进行误差校正。由于电离层是随时间和地点而变化的，因此，还没有一种模型能非常准确地反映电离层变化的真实情况。目前，单频接收机能通过8参数Klobuchar模型修正60%的电离层误差。

Klobuchar模型计算垂直电离层延迟的表达式为

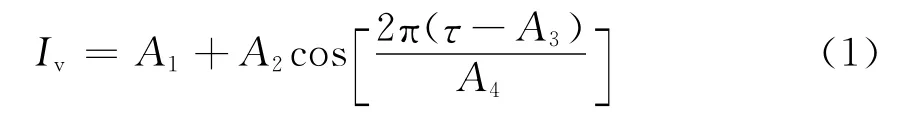
式中：A1＝5×10－9s（夜间值）；幅度A2＝α1＋为当地时；初始相位A3＝50400s（当地时14：00点）；周期A4＝β1＋β2φM＋＋，φM是电离层穿透点的地磁纬度，αi和βi（i＝1，2，3，4）是卫星广播的电离层参数。

电离层延迟随时间、地点的改变而变化。为各个较小的区域分别提供实时电离层改正是提高精度的有效途径，电离层格网改正技术文献［4]正是这样一种分别对各个小区域提供近乎实时电离层校正的方法，其计算过程如下：

1）每个广域参考站用双频接收机测量可见卫星的电离层延迟，并转换为对应的穿透点电离层垂直延迟及误差。穿透点（IPP）是指广域参考站接收机天线至卫星天线的连线与假想电离层球面的交点。以上数据实时地传送到广域中心站。

2）广域中心站利用所有广域参考站的电离层数据估计出每个电离层网格点（IGP）的垂直延迟及网格点电离层垂直改正误差GIVE值。GIVE定义为概率99.9%的误差限值。

3）这些网格点电离层改正数据经地面站上行传送给静地轨道卫星（GEO），数据更新周期为2～5min.GEO卫星再将改正数据播发给服务区内的用户。

4）用户接收到这些网格点电离层改正数据后，利用其电离层穿透点所在网格4个顶点的改正数据，用内插法求得用户的电离层延迟改正及误差，如图1，图2所示。

一定数量的地面参考站对卫星进行观测，在格网面上形成许多离散的穿透点。通过参考站数据处理，能按一定采样间隔给出这些穿透点的垂直延迟值。对于格网面上任一格点J，用其周围一定范围的穿透点，则可实时计算其相应的电离层垂直延迟值，同时得到延迟值的误差估计。

网格点电离层延迟的确定通常采用加权插值法，计算式如下

2 格网点电离层垂直改正误差传统算法

按照严格完善性要求 ，格网点电离层垂直改正误差（GIVE）是由一路数据形成的电离层延迟估计值与另一路的观测值之间的残差统计得到，按99.9%的置信度给定［5－6]。对于tk时刻的格网点延迟改正数将要应用的后一个更新间隔内（假定取5min）的任意时间t（tk≤t≤tk＋5），GIVE应以99.9%置信度保证与实际值IIGP（t）是一致的，即

在由各参考站的电离层延迟观测值计算网格点电离层延迟改正数时，假设参考站电离层延迟观测误差只含有偶然误差，插值模型没有误差，可按误差传递的方法估计网格点电离层延迟改正对应的GIVE.为保证完善性，将一路数据计算的电离层延迟改正应用于另一路观测数据进行验证，可得到更加准确的 GIVE.可由包围此点的相邻网格点垂直延迟值插值得到。

对于任一穿透点，选择包围该点的4个IGP点内插其延迟计算值，将穿透点的延迟观测值与计算值取差，即

在一个更新间隔内，用m个eIPP（t）构成一垂直误差序列，统计其误差限值，即

式中，

k为99.9%的置信分位数。

若包围IGP点的4个网格中至少有3个含有至少一条垂直误差序列，则可得到该IGP点的GIVE 值为［1]

式中，第一项为所有穿透点误差限值的最大值；第二项为网格点电离层延迟的绝对误差，由穿透点垂直误差序列插值计算得到，在插值计算时不需加入名义电离层模型，即

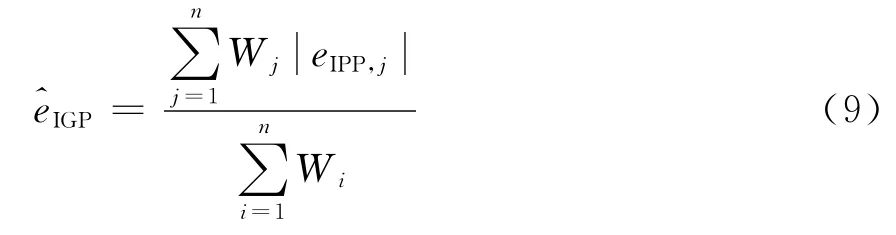
3 格网点电离层垂直改正误差改进算法

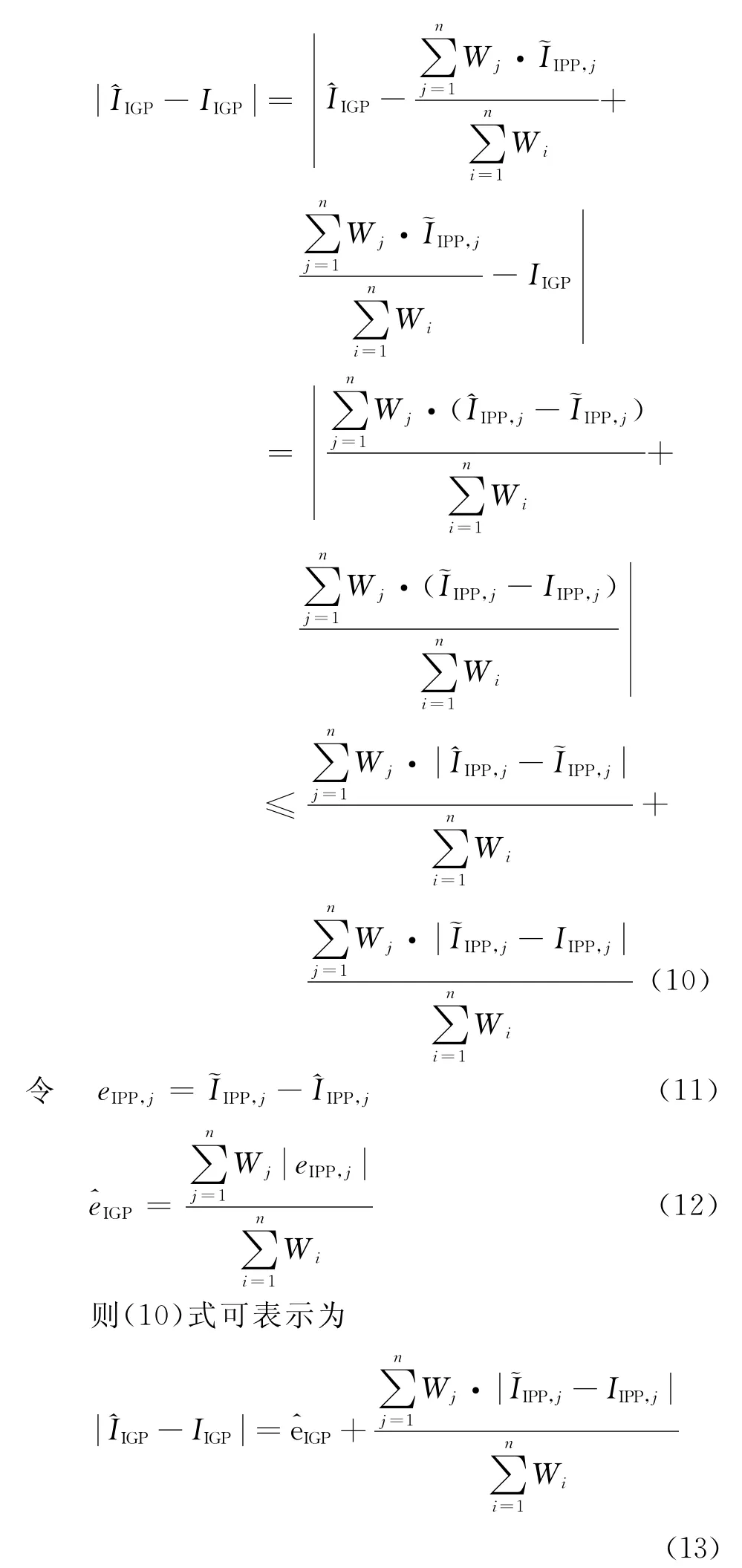
由前面的假设参考站电离延迟观测误差只含有偶然误差，插值模型没有误差，根据误差传递方法知是IIPP，j的无偏估计。可以用eIPP，j作为统计量对－IIPP，j进行估计。

将（8）式与（17）式比较可知 GIVEnew≤GIVE，GIVEnew在同样满足一定完好性风险概率的条件下比GIVE更加接近实际误差，从而提高了可用性。

4 算例分析

观测中国本土上空电离层在20°～40°（北纬）和100°～130°（东经）范围内，按5°×5°间隔，共计35个格点，高度为350km，观测时间为0～24h，按5min更新间隔和10s采样间隔计算GIVE及GIVEnew值，比较 参 数

对于一天的观测数据，取其中四个格点（1号，12号，26号，35号），其GIVE及GIVEnew值与实际误差随时间的变化如图3所示，GIVEnew值介于实际误差和GIVE值之间。对所有格点所有时间的RIGP和R′IGP进行统计如表1，各格点RIGP和R′IGP值都在0和1之间，且RIGP的均值皆小于R′IGP的均值。上述结果表明：在保证同样风险概率的条件下，GIVEnew值比GIVE值更加接近真实误差，其算法更优。

图3 GIVE及GIVEnew值与实际误差的比较

表1 不同算法RIGP与R′IGP统计

5 结 论

传统的电离层垂直改正误差算法由所有穿透点误差限值的最大值和网格点电离层延迟的绝对误差之和得来，该算法所得GIVE值具有极大冗余度。设计的改进算法通过对穿透点误差的加权，使得估计误差较传统算法更加接近真实误差，在保证一定风险概率的条件下提高了系统的可用性。

［1]ROTURIER B，CHATRE E C，VENTURA－TRAVESET T，et al.The SBAS integrity concept standardised by ICAO.application to EGNOS［J].ION GPS International Meeting of the Satellite Division，11－14Sept.2001，Salt Lake City，UT.2001：1838－1849.

［2]PARKINSON B W，AXELRAD P.Autonomous GPS integrity monitoring using the pseudorange residual［J].NAVIGATION，Journal of the Institute of Navigation，1988，35（1）：45－54.

［3]CURTIS A S，RICK N.Performance and availabilty analysis of simple local airport position domain monitor for WAAS［C]／／ION GNSS International Meeting of the Satellite Division，13－16Sept.2005，Long Beach，CA.2005：2837－2854.

［4]CHAO Yi－chang，YEOU－JYh T，TODD W，et al.An algorithm for inter－frequency bias calibration and application to WAAS ionospheric modeling［C]／／Proceedings of ION GPS－95，1995.

［5]陈金平.GPS完善性增强研究［D].郑州：解放军信息工程大学测绘学院，2001.

［6]牛 飞.GNSS完好性增强理论与方法研究［D].郑州：解放军信息工程大学测绘学院，2008.