有结构不确定的时延多智能体系统一致性
张 顺,杨洪勇
(鲁东大学 信息科学与工程学院,山东 烟台 264025)
所谓多智能体系统的一致性,是指随着时间的演化,一个多主体系统中所有主体的状态趋于一致[1]。对于多智能体系统的建模,Reynolds提出了Boid模型[2],但该模型的一些基本规则要求限制较多。Vicsek等人从统计力学角度提出了一个经典模型模拟粒子涌现的一致性现象。Jadbabaie等人最早对Vicsek提出的模型用矩阵方法进行了理论分析[3]。Olfati-Saber等人比较详细地提出了一致性问题的理论框架,并给出了基本的一致性协议,得到了多智能体系统取得平均一致的条件,而且分析了网络拓扑切换和系统存在时延的情况,给出了时延相关的一致性收敛条件[4]。Ren和Beard等人[5-7]同样考虑了一致性的基本问题,对一致性协议从连续时间和离散时间方面进行了描述,并且给出了时变拓扑平衡状态分析。
本文主要是采用LMI方法对具有时变结构不确定性的二阶时延多智能体系统的一致性进行分析,为获得相对较低的保守性,引入自由权矩阵的思想,得到了系统取得一致的判据。
1 问题描述
1.1 图论基础
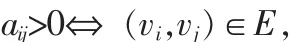

假设对于两个节点 i≠j,若存在下标集合{k1,k2,…,kl},且 aik1>0,ak1k2>0, …,ak1j>0 则称节点 i和节点 j之间存在一条有向连通路径。若对于图G中任意两个节点之间都存在至少一条有向连通路径,则称图G为强连通图。
1.2 一致性协议
用 xi(t)表示智能体的位置,vi(t)表示智能体 i的速度,假定任意智能体的状态方程为:
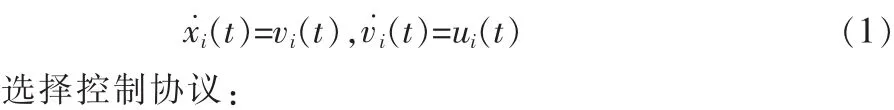
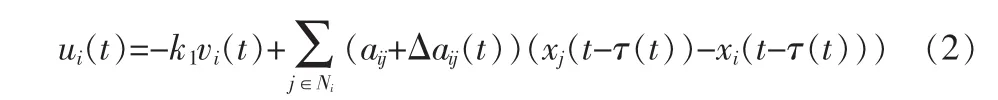
其中 k1>0 为速度的控制增益,Δaij(t)为多智能体系统时变结构不确定性,τ(t)为两个智能体之间的有界时变时延且满足:
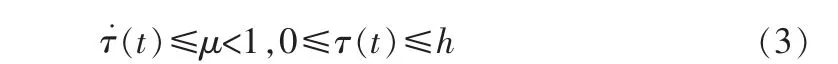
其中时延上界h>0。当且仅当任意智能体i,j状态方程满足条件(4)时,称控制协议(2)渐近可解二阶智能体系统(1)的一致性问题:

则有结构不确定性的二阶时延多智能体系统的状态方程可表示成如下矩阵形式:

引理1[9]给定具有适当维数的矩阵Q=QT,H,E则有:
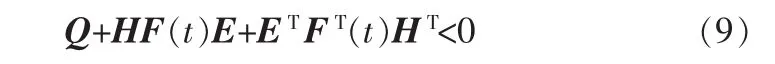
对所有满足 FT(t)F(t)≤I的 F(t)都成立的充要条件是存在一正数ε>0使得下式成立
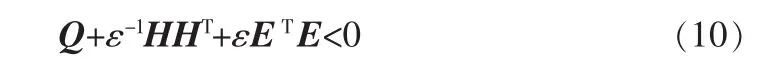
2 主要结论
对于时延满足式(3)有强连通拓扑结构的时变结构二阶时延多智能体系统:

则采用一致性协议(2)的多智能体系统(7)能够渐近实现平均一致,其中

证明:分成两步来证明,首先考虑无结构不确定性的二阶时延多智能体系统,即状态方程和控制协议满足
故如果 Ψ >0 且 [I]<0,对于充分小 ε 的有V˙(t,ξ)≤-ε‖ξ(t)‖2。满足时延约束(2)时,系统(16)是渐近稳定的。而利用shur补定理,得到 [I]<0 与

等价。
然后,在此基础上考虑系统(7),用 B′=-(L+Lc(t))⊗U=-(B+DF(t)Eb),替代(22)式中的 B,其中 D,Eb为常数矩阵,F(t)为未知的时变矩阵,且满足∀t>,FT(t)F(t)<I对应的式(22)变为


应用引理1,式(24)成立的一个充要条件是存在一个正数使得下边式(25)成立
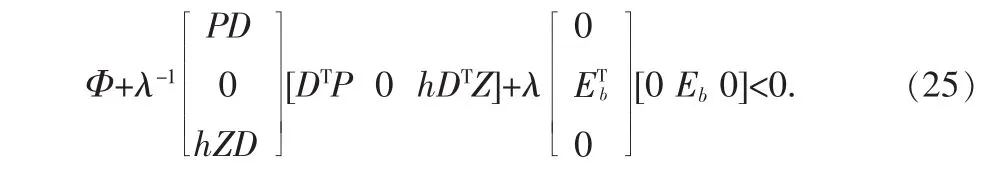
应用 shur补,式(25)等价于式(11)。
3 实例仿真
考虑如图1所标4个智能体组成的系统的强连通拓扑结构图,假定无结构不确定性的邻接矩阵取值为0,1。

图1 四智能体不同的拓扑结构形式Fig.1 Topology map of 4 agents
对图1中Ga所示的拓扑结构,采用控制协议(2)的二阶系统(1)仿真,令k1=2,取智能体间通信时延均为τ=0.3,初始状态位置 x(0)=[50-40-20 30]T,速度 V(0)=[3 2 4 8]。 根据定理1,可以知道,该具有结构不确定性的二阶时延多智能体系统最终会趋于稳定在图1所示拓扑基础上人为加入时变不确定性,拓扑为Ga的四智能体系统的各个智能体的位置变量和速度变量的演化仿真过程如下:
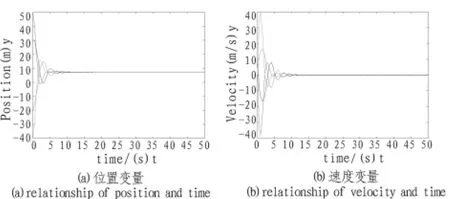
图2 多智能体系统一致性位置与速度与时间关系图Fig.2 Simulation of states of 4 agents
可以看到,各个智能体随着时间的变化位置(图2(a))趋向于某一固定值,速度(图2(b))收敛于 0。对于图1中拓扑Gb和其他未描述的拓扑结构,经过实验验证,得到类似结果;另外,对于在时延上界范围内的不同时延,也得到了类似的结果。
4 结 论
本文采用了时域分析方法研究了具有时变结构不确定性的时延二阶多智能体系统稳定性,主要用LMI方法进行了分析,并在推导证明结论过程中引入了具有较低保守性的自由权矩阵思想,而且考虑了系统实际应用过程中可能存在的结构不确定性的因素,得到了相关稳定性判据。
[1]杨文,汪小帆,李翔.一致性问题综述[C]//第25届中国控制会议,2006:1482-1486.
[2]Reynolds C W.Flocks,herds,and schools:a distributed behavioral model[J].Computer Graphics,1987,21(4):25-34.
[3]Jadbabaie A,JIE L,MORSE A S.Coordination of groups of mobile autonomous agents using nearest neighbor rules[J].IEEE Transactions on Automatic Control,2003,48(6):988-1001.
[4]Olfati-Saber R,Murray R M.Consensus problems in networks of agents with switching topology and time-delays[J].IEEE Transactions on Automatic Control,2004,49(9):1520-1533.
[5]WEI Ren,Beard R W.Consensus seeking in multiagent systems under dynamically changing interaction topologies[J].IEEE Transactions on Automatic Control,2005,50 (5):655-661.
[6]REN Wei.Multi-vehicle consensus with a time-varying reference state[J].Systems and Control Letters,2007,56 (7-8):474-483.
[7]WU Min,HE Yong,SHE Jin-hua,et al.Delay-dependent criteria for robust stability of time-varying delay systems[J].Automatica,2004,40(8):1435-1439.
[8]PENG Lin,JIA Ying-min.Consensus of a class of secondorder multi-agentsystems With time-delay and jointly-connected topologies[J].Automatic Control,IEEE Transactions on,2010,55(3):778-784.
[9]Petersen I R,Hollot C V.A riccati dquation approach to the stabilization of uncertain linear systems[J].Automatica,1986,22(4):341-397.

