Biostatistics in psychiatry(2)Effect size for continuous outcome measures
Baihua DUAB,Yuanjia WABG
Biostatistics in psychiatry(2)Effect size for continuous outcome measures
Baihua DUAB,Yuanjia WABG
As we discussed in our previous column[1], effect size is an important benchmark for the evaluation of treatment effects.W e discuss below several w idely used effect size measures for continuous outcome measures.(Effect sizes for dichotomous outcome measures will be discussed in a future column.)
For continuous outcomes,the observed effect size(OES)is defined as the difference between the treatment groups(experimental group vs.control group)in terms of the sample means,typically assessed at the end of the treatment(though this could be done at different times during the treatment and,to show the duration of the treatment effect,some time after completion of the treatment):
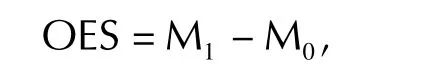
w here M1denotes the sample mean for the experimental group,and M0denotes the sample mean for the control group.The OES is often reported with an associated significance test and 95%CI,which is computed using the standard error of the OES(i.e.the standard deviation divided by the square root of the sample size;for the computation of confidence interval,see for example,Moore et al.[2]).
For many applications in psychiatry,the outcome of a study is based on the score of a psychometric scale which does not have a clear physical or physiological interpretation,making it difficult to interpret the OES.It is,for example,hard to know what a 1-point difference in the mean score of the Brief Psychiatric Rating Scale(BPRS)between groups means for the patients.In these situations a standardized effect size(SES)—which divides the observed differences in means by an appropriate standard deviation—is often used instead of the OES to facilitate the interpretation of the findings:

The SES can provide a useful interpretation for the treatment effect relative to the general patient population,in term s of how many SD’s the experimental group perform s better than the control group.
For normally distributed outcomes,the SES can be interpreted in terms of percentiles in the patient population(Whether or not the outcome is normally distributed can be evaluated using a histogram or various normality tests such as the Kolmogorov-Sm irnov test).For exam ple,if the mean level of symptom s in patients after standard treatment is at the 50th percentile of all patients who receive treatment and a new treatment decreases the mean level of symptoms by 1 standard deviation(i.e.,SES =1.0),then the mean level of sym ptoms of patients using the new treatment w ould be at the 16th percentile of all patients treated with standard treatment(based on the normal distribution),so 84%of persons using the standard treatment would have more severe symptoms than the mean level of symptom s in those using the new treatment.
There are several different SDs that can be employed when computing the SES:a pooled SD across the treatment groups,the SD from the control group(which is presumed to be more representative of the class of patients),or the SD from a separate study that administered the instrument to a large group of individuals representative of the class of patients.Cohen’s d[3]defines the SES using the pooled SD combined across the treatment groups, implicitly assuming that the within-group variances(and the SD’s)are homogeneous across groups. Glass’Δ[4,5]uses the SD for the control group,allowing the within-group variances(and the SD’s)to be heterogeneous across groups.More recently, Henson[6]com pared Cohen’s d versus Glass’Δ,and review ed their roles and interpretations in clinical studies.W e recommend that investigators regularly conduct a test for the homogeneity of the variances across groups,using procedures such as Levene’s test[7].This procedure serves two important purposes:1)if the variances are homogeneous the standard t test is em ployed but if heterogeneousSatterthwaite’s correction to the t test should be em p loyed;and 2)if variances are homogeneous the pooled SD is used in the com putation of SES(Cohen’s d)but if heterogeneous the SD from the control group is used(Glass’sΔ).
Both Cohen’s d and GlassΔuse internal estimates for the SD,based on the outcomes observed within the clinical study.But these SD’s might not be representative of the SD in the general patient population,because patient samples in most clinical studies are highly selected subgroups of patients.Johnston and colleagues[8]show ed how the eligibility criteria for a study could affect reported effect sizes.For exam ple,a clinical study that enrolls a homogeneous sample of patients using restrictive eligibility criteria might have a small internal SD for the scale used in the study and a correspondingly large SES,even though the OES m ight be modest.On the other hand,another clinical study that makes an effort to enhance its external validity(generalizability)by enrolling a diverse sample of patients m ight have a large internal SD and a small SES,even though the OES m ight be com parable to the OES in the first study.To avoid this inflation of the SES by the use of very homogeneous patient samp les,G lass[5]recommended(and w e concur)that whenever possible the SES be derived using an external estimate for the SD from a separate study that used the scale in a large representative sample of patients,such as the SD reported in the psychometric study that was conducted initially to norm the scale.
As an illustration,consider the follow ing hypothetical examp le for com puting OES and various versions of the SES.In a study comparing a new antidepressant to a standard antidepressant,the mean(SD)Ham ilton Depression Rating Scale(HAMD)at the end of treatment was 10.0(5.0)in the experimental group and 14.0(8.0)in the control group.The pooled SD for HAMD in the study was 6.7 and the SD for the HAMD in a large national study of depression is 7.5.The OES would be -4.0(10.0-14.0)points;Cohen’s d would be 0.60(4.0/6.7),Glass’Δwould be 0.50(4.0/8.0)and the SES using the SD from the external study SD would be 0.53(4.0/7.5).
Cohen[3]provided the follow ing rule of thumb to interpret the SES:d=0.2,0.5,and 0.8 are considered"small","medium",and"large".This rule of thumb is often used in the interpretation of clinical findings and in the power analysis and design of clinical studies.However,these are not absolute levels.The clinical interpretation of effect sizes needs to take into consideration the unique context for each treatment being studied:the incremental cost for the new treatment versus the standard protocol,the utility of benefits and side effects,and so forth.A"small"SES of 0.2 m ight be clinically significant for a low-cost intervention for a life threatening condition,while a"large"SES of 0.8 for a high-cost intervention for a minor clinical condition might not be clinically significant.W e will discuss clinical significance in a future column.
Although the SES is widely used in the psychiatry literature,the OES can be more informative than the SES for outcome measures that can be clearly related to physical or clinical entities,such as changes in weight,number of admissions,number of days in remission and so forth.For example, if at the end of a 6-month trial comparing a new community treatment for schizophrenia to usual treatment the mean(SD)number of days in remission of patients in the experimental group was 150(60)days and that of patients in the control group was 100(50)days,then the OES would be 50 days—which is quite easy to understand—but the SES(using the control group SD)would be 1.0, which is hard to interpret.
In the literature"effect size(ES)"is often used to refer to the SES.This can be confusing at times, making it unclear whether the OES or the SES is used.W e recommend that the terms"observed effect size(OES)"and"standardized effect size(SES)"be used to clarify the distinction between the two effect size measures.Ideally,the specific version of SD used for the SES should also be specified,such as"the SES based on the pooled SD", "the SES based on the control group SD",or"the SES based on the external SD from the xxx study"
1. Duan B,Wang Y.Significance tests and confidence intervals. Shanghai Archives of Psychiatry,2011,23(1):60-61.
2. Moore D,M cCabe G,Craig B.Introduction of the practice of statistics.Fifth Edition.Bew York:W.H.Freeman,2005:386-390.
3. Cohen J.Statistical power analysis for the behavioral sciences. Hillsdale,Bew Jersey:Law rence Erlbaum Associates,1988:24-27.
4. Glass GV.Primary,secondary,and meta-analysis of research. Educ Res,1976;5(10):3-8.
5. Glass GV.Integrating findings:the meta-analysis of research. Rev Res Educ,1977,5(1):351-379.
6. Henson RK.Effect-size measures and meta-analytic thinking in counseling psychology research.Couns Psychol,2006,34:601-629.
7. Levene H.Robust tests for the equality of variance.In I O lkin. Contributions to probability and statistics.Palo Alto,CA:Stanford University Press,1960:278-292.
8. Johnston MF,Hays RD,Hui KK.Evidence-based effect size estimation:an illustration using the case of acupuncture for cancer -related fatigue.BMC Com p lement Altern Med,2009,9:1-9.
Professor Naihua DUAN is Director of the Division of Biostatistics in the Department of Psychiatry at Columbia University Medical Center,Professor of Biostatistics at the Mailman School of Public Health at Columbia University,and a senior research scientist at the New York State Psychiatric lnstitute.His research interests include health services research,prevention research,sample design and experimental design,model robustness,transformation models,multilevel modeling,nonparametric and sem i-parametric regression methods,and environmental exposure assessment.Professor Duan has served as the Biostatistical Editor for the Shanghai Archives of Psychiatry since February 2011.
E-mail:naihua.duan@columbia.edu
Professor Yuanjia WANG is an assistant professor at the Department of Biostatistics in the Mailman School of Public Health at Columbia University,and a core member of the Division of Biostatistics in the New York State Psychiatric lnstitute.Her research interests include the general area of sem iparametric efficient methods for genetic epidem iological studies,developing statistical methods with applications in psychiatric research,variable selection methods,and design and analysis of clinical trials.Professor Wang has served as a member of the Editorial Board for the Shanghai Archive of Psychiatry since February 2011.
E-mail:yw2016@columbia.edu
10.3969/j.issn.1002-0829.2011.02.012
- 上海精神医学的其它文章
- 上海市网络成瘾中学生的应对方式与社会支持
- The subtypes of schizophrenia
- 轻度认知功能损害、阿尔茨海默病患者和健康对照者的枕区脑干听觉诱发电位的比较
- Comparison of the psychological status and quality of life of elderly urban Shanghai residents who receive different types of support services
- 精神医学科研方法(2)在招募研究对象前需要注册临床试验
- 论坛:DSM-5中拟去掉精神分裂症的亚型是否合理DSM-5中关于精神分裂症诊断标准修改的建议

