深表土冻结壁变形规律

郭永富

(中煤第五建设有限公司，河北邯郸 065003)

1 前言

我国山东、安徽、河南和河北等省，有14处以上煤田埋藏于400～1 000 m表土层之下。这些煤田上覆表土层有以下特点:黏土层厚度大、埋藏深(埋深达500～900 m)，第三、四系黏土层厚且含水量小，冻土抗压强度低，深部地温高达25～40℃。在十几年前就已发现了这些煤田，但一直未能开发［1］，主要原因就在于这些煤田为特厚表土层所覆盖，建井技术难度大。要在厚度400 m以上表土中建井，可靠的方法只有冻结法和钻井法。钻井法受设备和条件所限，大直径井筒只能采用冻结法施工。

截至2004年年初，世界上主要使用冻结法的国家中，凿井最大冻结深度是930 m(英国)，冻结法凿井通过表土层最厚的是苏联雅可夫列夫铁矿副井，表土厚度达571 m。

我国自1955年首次采用冻结法凿井技术以来，截至2004年年初已施工立井500多个，总延米达100 km以上。在当时已竣工的井筒中，最大冻结深度为488 m，穿过的最厚表土层为459 m。

值得指出的是，我国一些深冻结井在建设期间冻结壁或井壁均不同程度地出现了问题。

1)梁宝寺煤矿主井:在垂深300 m左右处外层井壁破裂，井壁缩径，冻土进入井内，不得不回填井筒，重新施工井壁。

2)程村煤矿副井:在垂深230 m处发生冻结管断裂事故。

3)济西煤矿副井:在垂深371 m处发生冻结管断裂事故，底膨严重、井帮开裂。

由此可见，用冻结法通过400 m深表土层，尚存在不少技术上的问题。而要用冻结法通过近600 m深表土层，则有更多、更复杂的技术问题需要研究解决［2］。

鉴于此，文章以目前国内外冻结法通过表土最深的郭屯主井冻结工程为背景，介绍深表土层冻结法凿井技术的基础研究工作。该项目研究始于2004年，通过该项目的研究与应用，已顺利地施工了郭屯主井587.5 m，口孜东风井573 m等多个500 m以上表土冻结工程。

目前国内外对深厚表土冻结壁的受力及变形等基础研究不多，对各参数之间的相互影响关系研究不深，为此利用ANSYS软件，针对深部黏土地层，开展地压、冻结壁厚度、平均温度、掘砌段高4个主要因素对冻结壁变形影响的数值模拟计算，以此分析各参数的影响规律。

2 井筒掘砌施工数值模型

2.1 基本假设

为方便建模及分析研究［3］，做以下假设:a.冻结壁厚度及冻结温度场的径向分布规律沿井筒圆周方向处处相同;b.井筒施工无超、欠挖，外壁与冻结壁接触状态沿井筒圆周方向处处相同。

2.2 模型特征

基于上述假设，利用ADPL语言建立参数化的“冻结凿井施工”轴对称有限元模型［4］(见图1)。

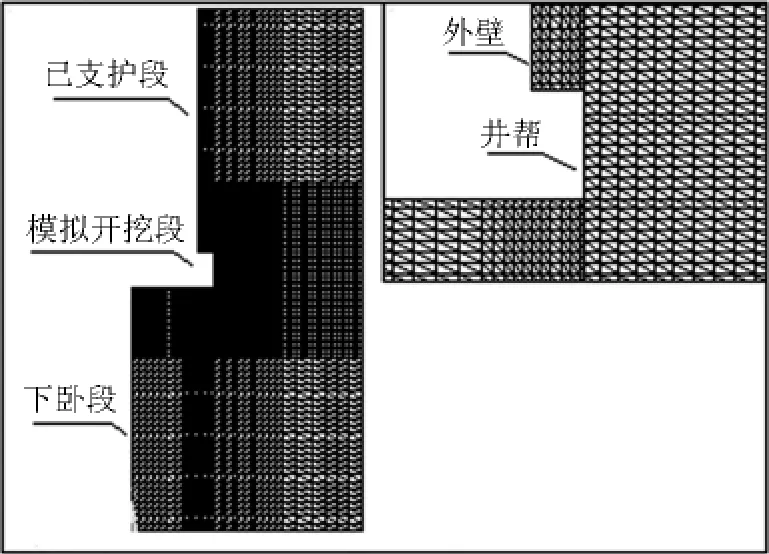
图1 井筒掘砌施工过程的轴对称有限元模型Fig.1 Models of axisymmetrical finite element during shaft sinking

模型由上部已支护段、中间开挖段和底部下卧段三部分组成。

由于采用参数化方法建立，模型具有以下特点:a.具有井筒、井壁、冻结壁几何特征、地层土性的广泛适应性;b.能够模拟任意段高的分层开挖与支护，掘、砌时间可调。

2.3 边界条件与荷载

根据冻结凿井中冻结壁的变形特点，模型底部边界施加竖向位移约束(UY=0)。

上覆地层自重根据地层深度及土层平均容重计算后直接施加在模型顶面上;水平地压按P=0.012H(单位:MPa;其中H为地层深度，单位:m)确定后施加在右侧竖向边界上。

2.4 材料模型及参数

2.4.1 外层井壁

外层井壁可视为线弹性介质，而且外壁浇筑后混凝土弹性模量、泊松比都随时间延长而增长。混凝土弹性模量与泊松比分别按E=40 GPa、μ=0.2取值。

2.4.2 冻土

冻土的弹塑性本构采用双线性强化模型。屈服强度按冻土试样单轴抗压强度的1/2～2/3取值，强化(塑性)段模量为弹性模量的1% ～3%。

冻土蠕变采用以下常用方程描述，该方程描述的实质为第一阶段蠕变:

式(1)中，εc为蠕变应变;At为与温度有关的蠕变参数，(MPa)－1·h－1;B、C 为与应力、时间有关的无量纲蠕变参数;σ为蠕变应力，MPa;t为蠕变时间，h。

由于冻结壁蠕变属于三维应力下的蠕变，单轴蠕变试验参数应先转换为三轴蠕变参数方可使用。冻土的强度、变形和蠕变值见表1和表2。

表1 冻土的弹性模量及泊松比Table 1 Modulus of elasticity and Poisson ratio of freezing soil

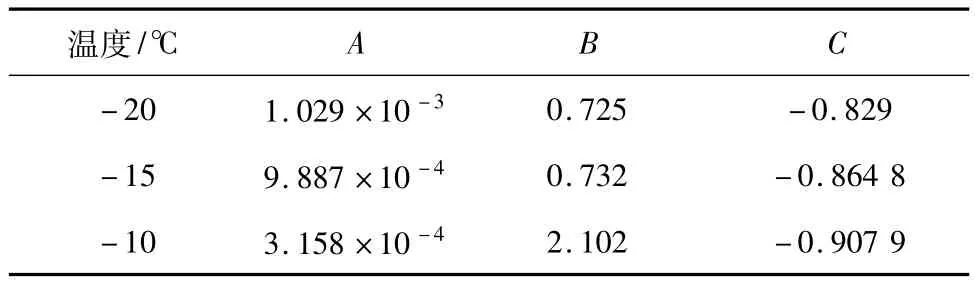
表2 冻土蠕变参数Table 2 Triaxiality creep parameter of freezing soil

2.5 模拟计算方案

2.5.1 参数的取值和计算方案规划

数值计算中不同参数的取值如下:a.地层深度分别按350 m、550 m取值;b.掘砌施工段高分别按2 m、3 m、4 m取值;c.冻结壁平均温度分别按－15℃、－25℃取值;d.冻结壁厚度分别按10 m、14 m取值;e.水平地压按 P=0.012 H(单位:MPa)取恒定值;f.掘砌施工时间按同一施工方案进行，掘进、支护时间均完全相同。

对上述因素的不同取值进行全组合，得到最终的数值计算方案规划(见表3)。

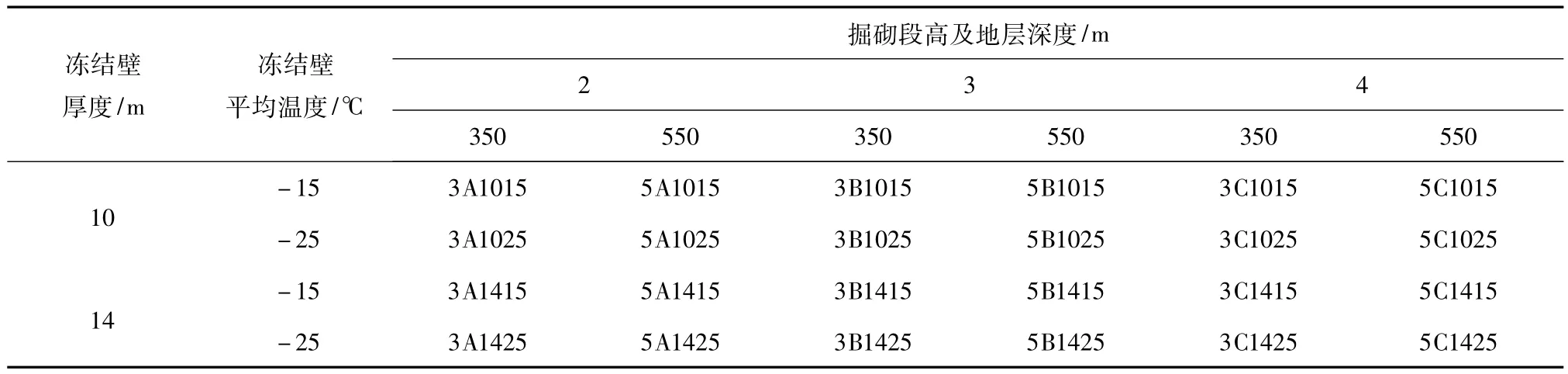
表3 冻结壁变形规律的计算方案规划Table 3 Numerical procedure of distortion disciplinary of frozen wall

2.5.2 掘砌模拟步骤

1)冻结温度场的模拟［5］。通过内、外部边界温度赋值，而后进行稳态温度场计算，模拟井内土体、冻结壁土体内的冻结温度场分布状态。

2)地层初始自重应力场的模拟。受地层温度不均及力学参数温度非线性的影响，自重应力场只能近似模拟。

3)井筒开挖支护过程的数值模拟。自重应力场模拟后，逐段高分层开挖，模拟实际掘砌施工过程。每个段高的开挖及钢筋绑扎时间为20 h，支护8 h，即28 h完成1个循环。各段高均采用分层开挖，层厚0.25 m，每段高分10次完成开挖，井壁砌筑一次性浇筑完成。

3 计算结果及分析

3.1 井帮位移

井帮蠕变位移的计算值见表4。

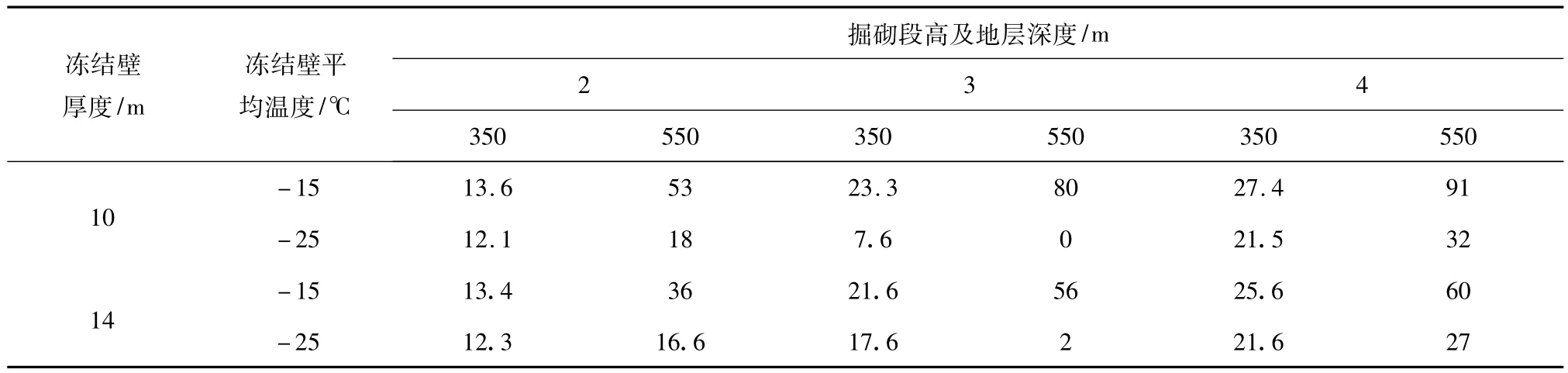
表4 井帮蠕变位移计算值(单位:mm)Table 4 Calculated value of creep displacement of shaft wall(unit:mm)

基于上述数值计算结果，对影响井帮位移的各主要因素分别分析如下。

3.2 冻结壁平均温度对井帮位移的影响

本数值模拟仅取了－15℃、－25℃两种冻结壁平均温度开展计算研究。井帮蠕变位移与冻结壁平均温度关系曲线见图2、图3。

由计算结果可见:在其他因素不变的条件下，井帮蠕变位移随冻结壁平均温度下降而减小;“井帮蠕变位移～冻结壁平均温度”呈现出明显的非线性变化关系;其非线性程度随地层深度(地压)增加而变得更加显著。

分析认为:冻结壁变形的上述趋势与“冻土强度～冻土温度”之间的非线性关系有关。冻结温度降低至一定值后，随温度下降，冻土变形模量增幅趋缓，导致冻结壁温度下降过程中，井帮位移的减小幅度也相应减小。

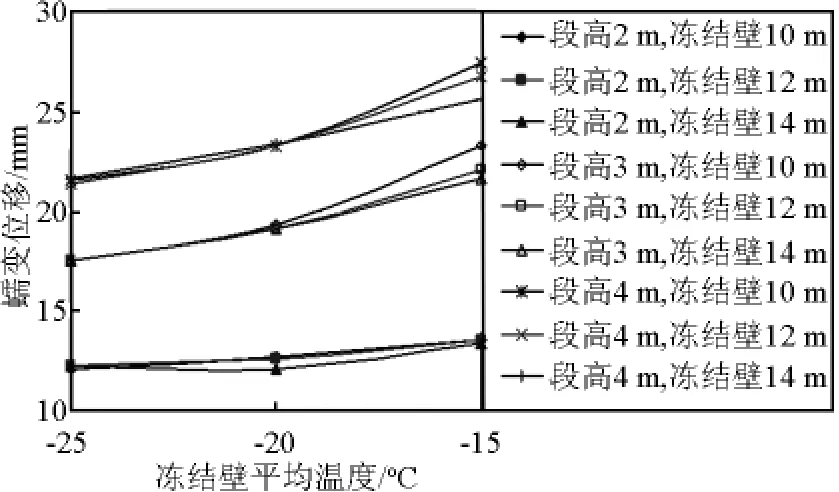
图2 井帮蠕变位移与冻结壁平均温度曲线(350 m)Fig.2 Curve of creep displacement of shaft wall and temperature of frozen wall(350 m)

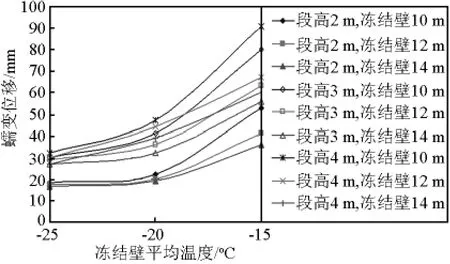
图3 井帮蠕变位移与冻结壁平均温度曲线(550 m)Fig.3 Curve of creep displacement of shaft wall and temperature of frozen wall(550 m)

为便于更直观地分析冻结壁降温对抑制井帮位移的效果，忽略－15～－25℃“井帮位移～冻结壁温度”的非线性，计算出冻结壁单位降温造成的井帮位移减小量，见表5。

由表5中数据可见:单位降温条件下，段高为2 m，地层深度为350m时，井帮位移减小幅度最小(总位移减小幅度不足1 mm)，表明该条件下降低冻结壁温度对井帮变形意义不大。原因应在于:对于350 m深度的地层，其冻结壁强度、厚度均满足甚至超过了实际工程的需要。因此，进一步降温或增大冻结壁厚度不仅效果不明显，而且将造成浪费。

相比之下，段高为4 m，地层深度为550 m时，冻结壁单位降温可使井帮总位移减小15.5～31.8 mm，弹塑性位移减小12.2～25.9 mm，蠕变位移减小3.3～5.9 mm。由此可见，高地压、大段高施工的条件下，降低冻结壁温度对减小井帮位移效果显著。

综上所述，特厚表土层中冻结壁设计时，可首先考虑通过降低冻结壁温度，提高冻结壁整体强度与刚度，以减小冻结壁变形。此外，考虑到“井帮位移～冻结壁温度”之间关系的非线性，即随着温度的降低，冻结壁降温对井帮变形的抑制效果将逐渐减小，则在冻结壁温度下降至一定程度后，仍试图通过大幅度降温控制冻结壁的变形是不合理的，必须考虑采用其他措施(如控制井筒掘砌施工段高、调整冻结壁设计厚度)。

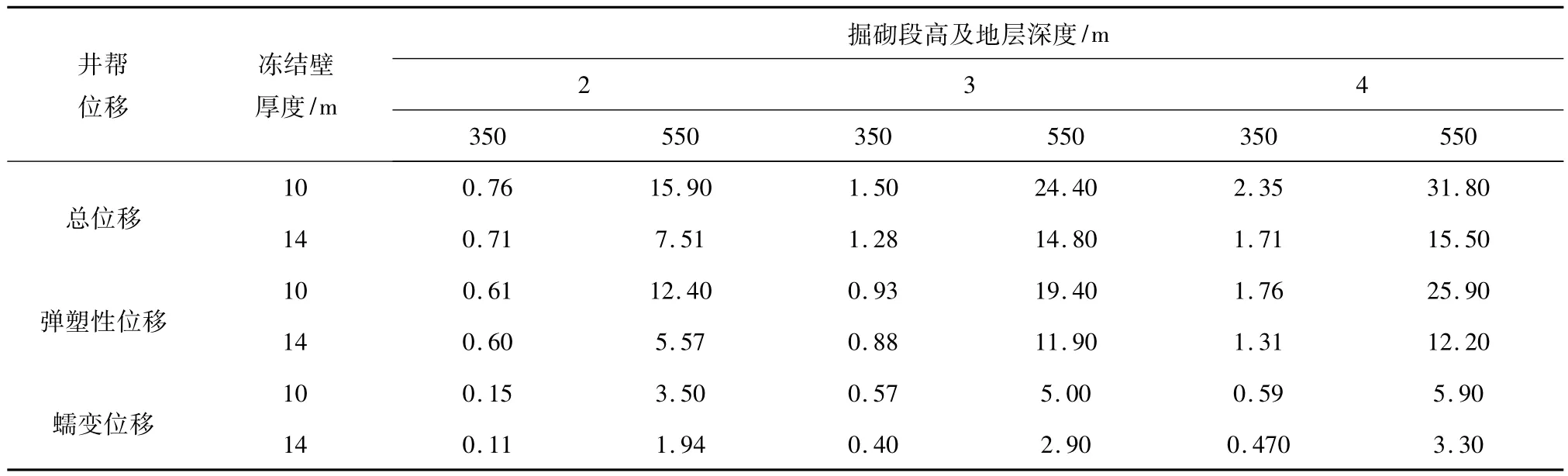
表5 冻结壁单位降温造成的井帮位移减小量(单位:mm)Table 5 Decrement of wall displacement caused by unit temperature decreasing of frozen wall(unit:mm)

3.3 冻结壁厚度对井帮位移的影响

井帮位移与冻结壁厚度关系曲线见图4～图7。

由计算结果可见:其他因素不变时，井帮位移随冻结壁厚度增大而减小;但减小幅度不仅与冻结壁平均温度有关，也和地层深度(即水平地压)有关，即井帮蠕变位移的非线性程度随深度增加、温度升高而更显著。

例如:通过计算可知地层深度为550 m，掘砌段高为4 m的条件下，如果冻结壁温度保持－15℃不变，冻结壁厚度由10 m增大到14 m，则井帮弹塑性位移由 436 mm减小至 252 mm，减小幅度为184 mm。同样当冻结壁温度为－25℃时，井帮弹塑位移减小幅度仅为46 mm。

相比之下，地层深度为350 m，掘砌段高为4 m的条件下，如果冻结壁温度为－15℃不变，冻结壁厚度按同样的幅度增大，井帮弹塑性位移仅由59.3 mm减小至51.7 mm，减小幅度为7.6 mm。

上述现象进一步证实:冻结壁整体强度、刚度(取决于冻结壁厚度及平均温度)增大至一定程度后，继续增大冻结壁厚度对减小井帮变形效果将明显降低。

类似地，为便于更直观地分析冻结壁厚度变化对井帮位移的影响，计算出冻结壁单位厚度增量(1 m)造成的井帮位移减小量，见表6。

图4 井帮蠕变位移与冻结壁厚度曲线(350 m)Fig.4 Curve of creep displacement of shaft wall and frozen wall thickness(350 m)

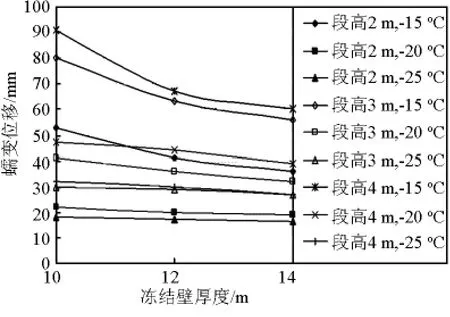
图5 井帮蠕变位移与冻结壁厚度曲线(550 m)Fig.5 Curve of creep displacement of shaft wall and frozen wall thickness(550 m)

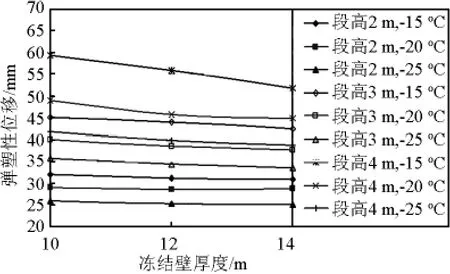
图6 井帮弹塑性位移与冻结壁厚度曲线(350 m)Fig.6 Curve of elastoplastic displacement of shaft wall and frozen wall thickness(350 m)

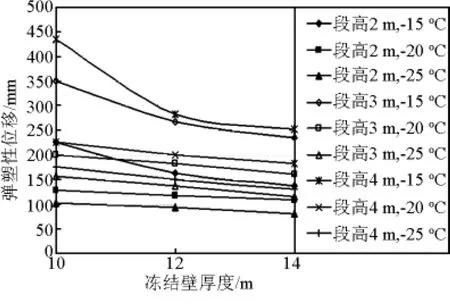
图7 井帮弹塑性位移与冻结壁厚度曲线(550 m)Fig.7 Curve of elastoplastic displacement of shaft wall and frozen wall thickness(550 m)

表6 冻结壁单位厚度增量造成的井帮位移减小量(单位:mm)Table 6 Decrement of wall displacement caused by unit thickness increment of frozen wall(unit:mm)

由表6中数据可见:冻结壁厚度在10～14 m范围内变化时，单位厚度增量(1 m)造成的井帮位移减小量，以地层深度为550 m，井帮温度为－15℃时最明显;随着井帮温度降低、施工段高缩小，增大冻结壁厚度对于减小蠕变位移效果越来越不明显。此外，冻结壁厚度的增大仅导致蠕变位移量的小幅度减小，表明冻结壁蠕变位移量对冻结壁厚度的变化不敏感。

在本数值模拟中各参数的取值(冻结壁温度为－15～－25℃，冻结壁厚度为10～14 m)条件下，增大冻结壁厚度对于减小井帮变形的效果不比降低冻结温度明显。因此，综合分析可见:与增大冻结壁厚度相比，降低冻结壁平均温度能更经济、有效地减小冻结壁的变形。

所以冻结壁设计中，应首先考虑尽量降低冻结壁平均温度，以提高冻结壁整体强度与刚度，实现控制冻结壁变形的目的［6］;只有在冻结壁降温对提高冻土强度影响甚小，或现有技术条件无法继续降低冻结壁温度时，方适合通过增大冻结壁厚度提高冻结壁的强度与刚度。

3.4 掘砌施工段高对井帮位移的影响

井帮蠕变位移与掘砌段高关系曲线见图8和图9。

图8 井帮蠕变位移与掘砌段高曲线(350 m)Fig.8 Curve of creep displacement of shaft wall and sinking stage height(350 m)

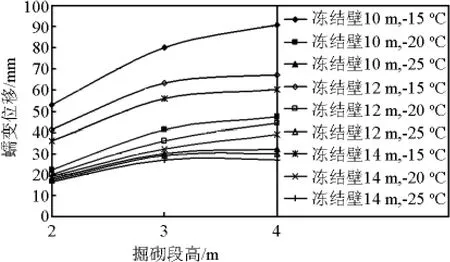
图9 井帮蠕变位移与掘砌段高曲线(550 m)Fig.9 Curve of creep displacement of shaft wall and sinking stage height(550 m)

由图8和图9中的曲线可见:在其他因素不变的条件下，井帮位移随掘砌施工段高的增大而增大，“井帮位移～掘砌施工段高”之间同样具有明显的非线性特征;非线性程度与冻结壁平均温度、地层深度(代表了原始地压)有关［7］。具体而言，冻结壁温度越高、地层深度(原始地压)越大，“井帮位移～掘砌施工段高”之间的非线性特征越明显。

分别将井筒掘砌段高为3 m、4 m时的井帮位移计算值与段高为2 m条件下的计算值求比值，可得表7中的数据。

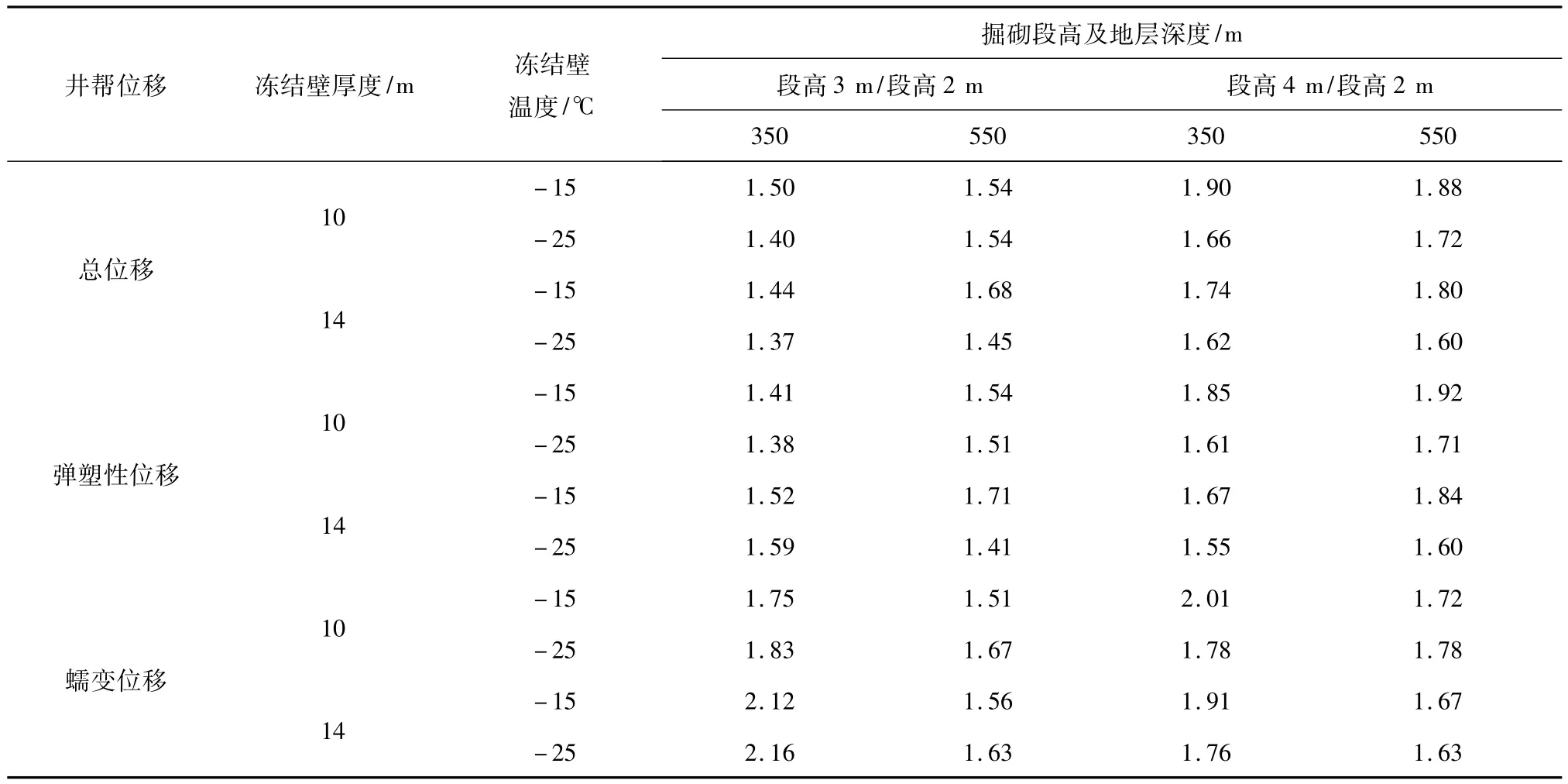
表7 不同段高条件下的井帮位移计算值之比Table 7 Ratio of calculated displacement value of shaft wall at different stage height

由表中数据可见:掘砌施工段高由2 m增加到3 m的情况下，井帮总位移、弹塑性位移的增幅均多在40% ～60%;而段高由2 m增加到4 m时，井帮总位移的增幅多在70% ～90%，弹塑性位移的增幅多在60%～80%。

掘砌段高同样增长的条件下，井帮蠕变位移量增幅相对较大，说明在其他条件不变时掘砌段高对井帮位移影响较大，施工中可通过调节施工段高来控制冻结壁变形，保证井筒安全。

3.5 地层深度对井帮位移的影响

不同段高条件下的井帮位移与水平地压关系曲线见图10～图12。

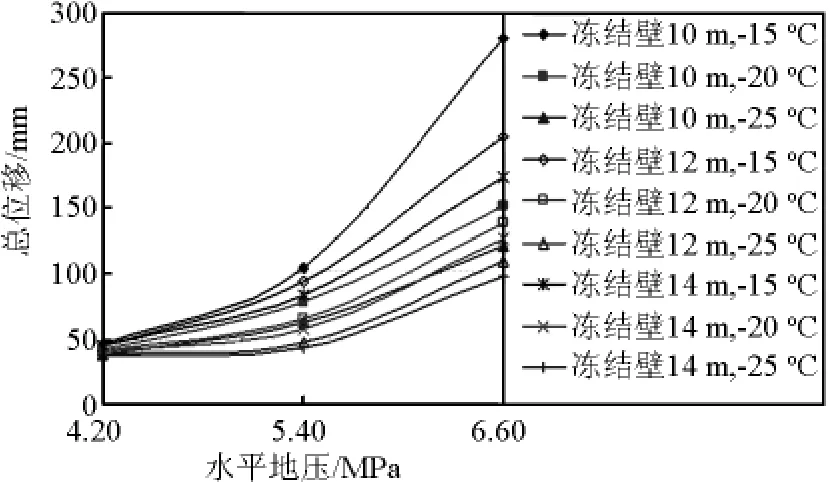
图10 井帮总位移与水平地压曲线(段高2 m)Fig.10 Curve of total displacement of shaft wall and horizontal ground pressure(stage height 2 m)

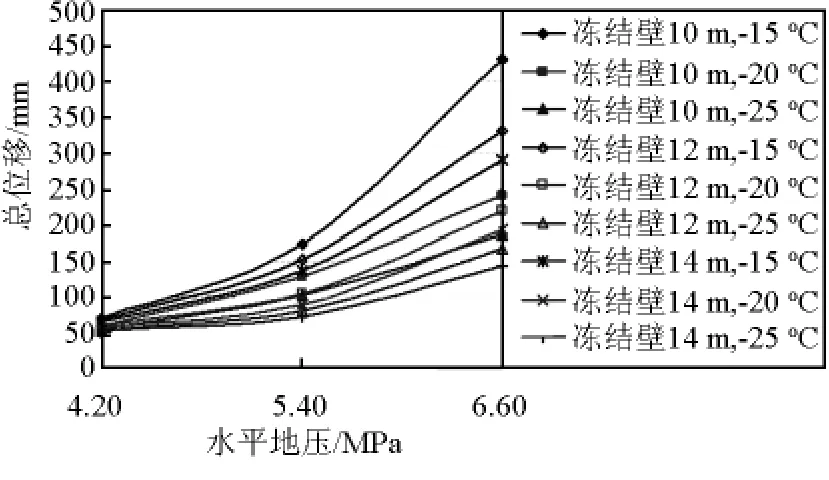
图11 井帮总位移与水平地压曲线(段高3 m)Fig.11 Curve of total displacement of shaft wall and horizontal ground pressure(stage height 3 m)

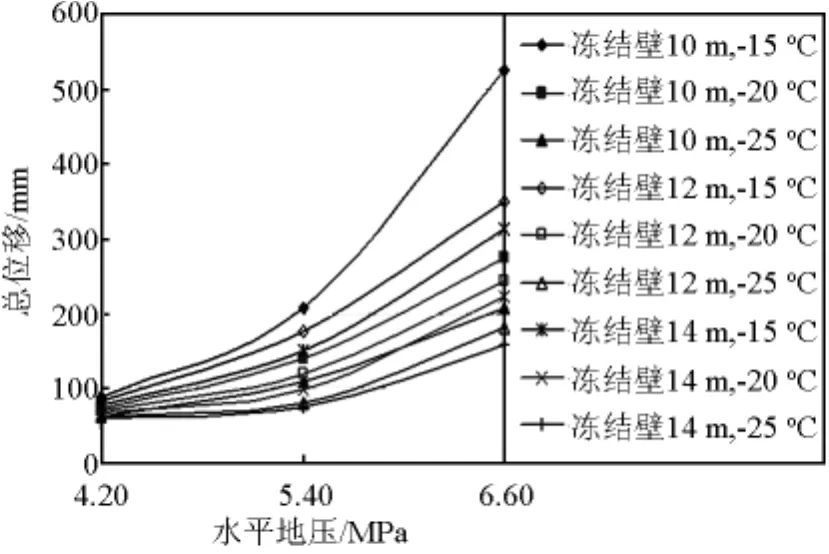
图12 井帮总位移与水平地压曲线(段高4 m)Fig.12 Curve of total displacement of shaft wall and horizontal ground pressure(stage height 4 m)

由图示曲线可见:同一段高条件下，井帮位移随水平地压(地层深度)的增大而增大，“井帮位移～水平地压”之间同样具有明显的非线性特征;冻结壁厚度越小、冻结壁温度越高，则“井帮位移～水平地压”之间的非线性程度越明显。

具体而言，其他条件相同的情况下，地层深度由450 m增加到550 m时，井帮位移增量远大于地层深度由350 m增大到550 m时的变化值，并且以冻结壁厚度为10 m，温度为－15℃时冻结壁变形的变化幅度最大。不难理解，上述现象的出现与该条件下冻结壁的总体强度及刚度最小密切相关。

同时，由图示曲线可见:与冻结壁厚度变化、掘砌段高变化相比，地层深度，即地压变化对冻结壁变形的影响更为显著。

4 结语

通过对于不同冻结壁温度、冻结壁厚度、掘砌施工段高、地层深度(代表水平地压)取值条件下，冻结壁变形的数值模拟及分析，可以得到如下结论:

1)冻结壁表面位移，即井帮位移，随着冻结壁平均温度的降低、冻结壁厚度的增大而减小，随掘砌施工段高的增大、地层深度(水平地压)的增大而增大。地压值对于冻结壁变形影响最为显著。井帮位移与上述因素间均呈现非线性关系特征，且各因素间存在相互影响。

2)在冻结壁厚度为10～14 m，冻结壁平均温度为－15～－25℃的前提下，与增加冻结壁厚度相比，降低冻结壁平均温度对于减小井筒开挖过程中的井帮变形更为经济、合理。

3)在进行深井冻结壁的设计时，应首先考虑通过降低冻结壁平均温度提高冻结壁的整体强度与刚度，以控制井帮变形，确保冻结壁及冻结管的安全;其次是增大冻结壁厚度。

4)按变形条件开展冻结壁设计时，掘砌段高是重要且必不可少的参数。在其他条件不变时掘砌段高对井帮位移影响较大，施工中可通过调节施工段高来控制冻结壁变形，为此，应根据地层条件，结合可能的施工工艺，确定合理的掘砌施工段高，确保冻结壁的安全。

［1］洪伯潜.巨野煤田开发条件及井筒施工关键技术［J］.中国煤炭，2002(4):20－23.

［2］陈湘生.对深冻结井几个关键问题的探讨［J］.煤炭科学技术，1999(1):20－23.

［3］崔广心.冻结壁厚度和变形规律的模型试验研究［J］.煤炭学报，1992(3):67－69.

［4］王衍森，杨维好.深部土人工冻土力学特性的试验研究方法探讨［J］.建井技术，2003(5):34 －37.

［5］王衍森，杨维好，任彦龙.冻结法凿井冻结温度场的数值反演与模拟［J］.中国矿业大学学报，2005(5):38－41.

［6］崔广心.深厚冲积层中冻结壁厚度的研究［J］.冰川冻土，1995(s1):20－23.

［7］张开顺，李炳胜，杨维好，等.井筒冻结壁径向位移规律计算研究［J］.中国煤炭，2005(11):29－32.