往复式冰箱压缩机吸气阀片模态参数测量及分析

尹亦阳，冯 涛，王 晶，邱 辰，刘 娜，胡宏梁，张 力

（北京工商大学 材料与机械工程学院，北京 100048）

0 引言

压缩机是冰箱的主要噪声源，阀片是安装在压缩机气缸上控制气体进出的部件，它交替开启与关闭阀座气体通道，控制着压缩机的吸气、压缩、排气和膨胀四个过程。吸气阀片是压缩机的重要组成部件，也是易损件，直接影响压缩机的性能。如果设计不当，会增大吸气阀片疲劳断裂的可能，并增大其辐射噪声。因此，对压缩机吸气阀片进行实验及理论模态分析，掌握其振动特性，对提高压缩机工作性能和可靠性、降低压缩机辐射噪声具有重要意义。

往复式冰箱压缩机吸气阀片属于轻薄弹性体，常规的模态实验方法对其并不适用，其振动激励方式及振动量的测量方法均需重新考虑，以减少测量方法对待测对象振动特性的影响。对于轻薄弹性体的实验测量，李雷[1]等人采用了声激励方式对薄铝板的模态参数进行了识别，得到了与传统激励方法基本一致的固有频率和振型。钟旋[2]等人利用激光测振方法测试了扬声器箱体振动速度随频率的变化规律，进而改进了小型扬声器系统的声学特性。针对往复式冰箱压缩机吸气阀片的结构特性，本文提出了应用声激励进行激振，应用激光测振仪测量吸气阀片振动响应的模态实验方案，并与理论模态计算进行了比较。

1 模态分析理论概述

模态分析是研究结构动力特性的一种方法，是系统辨识方法在工程振动领域中的应用。模态是机械结构的固有振动特性，每一阶模态具有特定的固有频率、阻尼比和振型。如果是通过实验将采集的输入与输出信号经过参数识别获得系统模态参数，称为实验模态分析;如果是由有限元计算的方法取得，则称为理论模态分析。本文采用了LMS Test. Lab实验模态分析软件对压缩机吸气阀片进行了模态参数识别，并与LMS Virtual. Lab的理论模态计算结果进行比较。

振动模态是弹性结构固有的、整体的特性。如果通过模态分析方法搞清楚了结构在某一易受影响的频率范围内各阶主要模态的特性，就可能预测结构在此频率范围内外部或内部各种振源作用下的实际振动响应。因此，模态分析是结构动态设计及设备故障诊断的重要方法。

根据李德葆等人[3]的研究，频率响应函数矩阵的表达式为

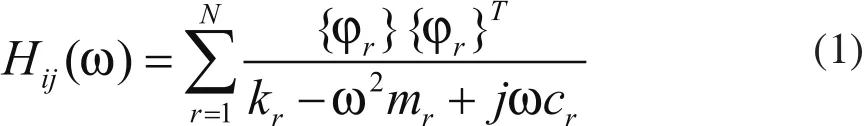
其中Hij表示激励第j点时第i点的频率响应函数，为模态振型，kr为第r阶模态刚度系数，Cr为第r阶模态阻尼系数，ω为固有频率，ωr为第r阶固有频率，mr为第r阶模态质量。

将式(1)展开可得

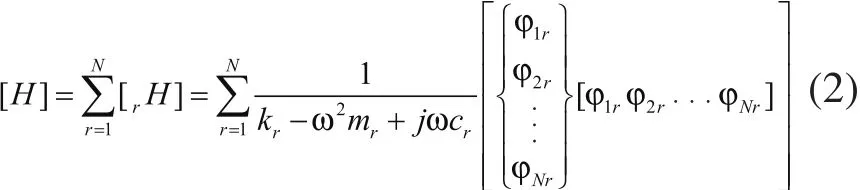
式中[rH]为第r阶模态的频响函数矩阵。

取式(2)响应函数矩阵中的任一列

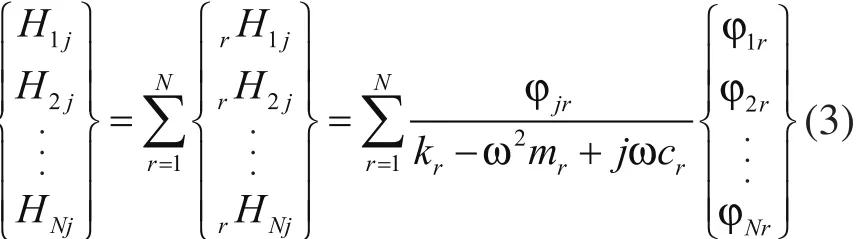
由式(3)可见，[H]中的任一列即包含全部模态参数，而该列的r阶模态的频率函数之比值，即为r阶模态振型:

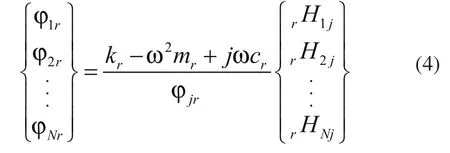
由式(4)可知，如果在某一固定点j处激振，而在其他各点拾振，便能得到频响矩阵的一列，这一列频响函数中即可包含进行模态分析的全部信息。本文即是使用体积声源对吸气阀片进行单点激励，移动激光测点测出一列21个频响函数，经最小二乘复指数LSCE算法识别得到吸气阀片模态参数的。

2 吸气阀片模态实验系统设计

某型号往复式冰箱压缩机吸气阀片形状如图1所示，阀片长50mm，宽42mm，厚0.2mm，属于轻薄弹性体。对于轻薄弹性结构体的测量只能考虑非接触方式的激振和拾振[4]。

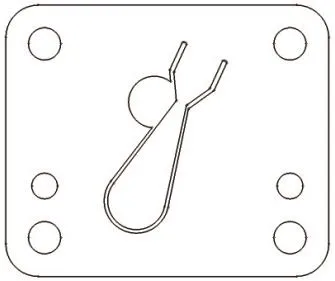
图1 某型号往复式冰箱压缩机吸气阀片平面简图

根据轻薄弹性体模态实验测量的需要，决定使用LMS体积声源对吸气阀片进行声激励，使用Polytek激光测振仪测量吸气阀片的振动响应，实验测量方案如图2所示；实验测量系统由压缩机吸气阀片样件、加速度体积声源、激光测振仪、LMS信号采集前端及计算机等五部分组成。

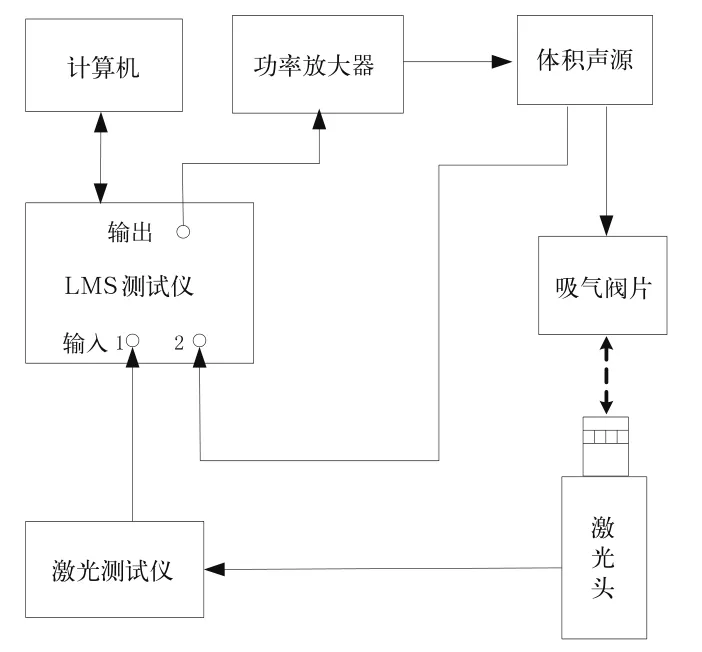
图2 实验测量系统结构示意图

吸气阀片采用如图3所示的刚性支撑装夹方式。刚性支撑是将试件刚性的固结在质量大、刚度高的虎钳上，此法通常适合于测量分析试件的低阶模态，高阶模态常由于连接刚度的改变和基础振动模态的影响造成精度和重复性差。激光测点在压缩机吸气阀片上的位置分布如图4所示。

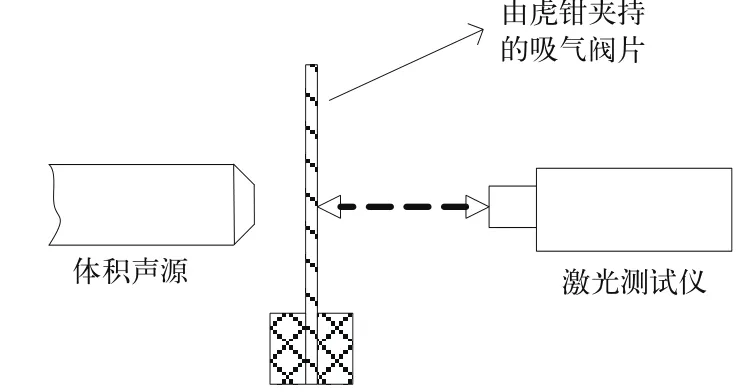
图3 吸气阀片的装卡方式

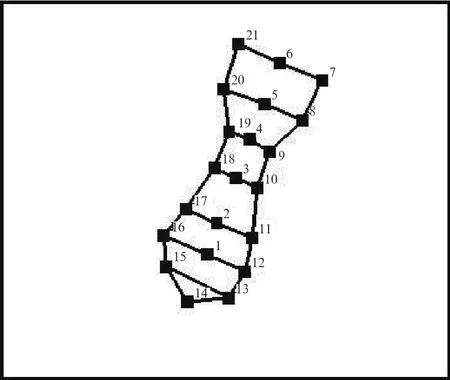
图4 激光测点在吸气阀片上的分布

检查各仪器接线无误后，启动LMS测振仪、体积声源的功率放大器以及激光测振仪数据处理平台，调整激光测振仪的水平竖直位置，使其高度与压缩机吸气阀片测点中心处等高，使用自动对焦功能将激光测振仪的激光测点聚焦，当激光测振仪信号满格时，停止调节，锁死激光测振仪。激励信号采用200～4096Hz宽带噪声。

3 模态实验数据测量及分析[5]

利用LMS Test. Lab的建模软件建立一个吸气阀片的平面模型，进行振动数据采集，然后利用最小二乘复指数LSCE算法对所采集的数据进行分析，得到吸气阀片的固有频率和阻尼比。

在体积声源的宽带噪声激励下，通过移动激光测点，测得21组频响函数，这21个频响函数就是式(4)中频响矩阵的一列。图5为测点1的频响函数，此频响函数相当于式(4)中的[rH1j]。LSCE算法就是通过对频响矩阵的一列的识别而得到吸气阀片模态参数的，LSCE算法识别模态参数的优势在于可以处理低阻尼结构的模态分析，不受数值不稳定性和频率范围限制的影响，并且能够得到比较清晰的稳态图，因此该算法是单带宽分析的通用方法。

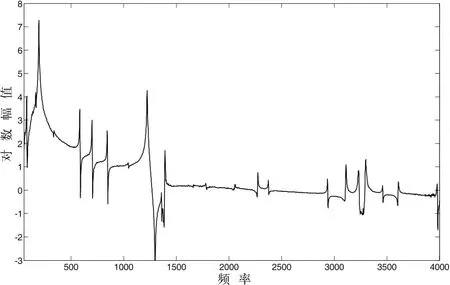
图5 测点1的频响函数

应用LMS Test. Lab软件中的LSCE算法对测得的频响函数进行分析，结合宽带噪声激励下压缩机吸气阀片数据的稳态图我们可以获取系统的各阶固有频率和阻尼比信息。LSCE算法识别出的吸气阀片的前四阶的固有频率和阻尼比如表1所示，前四阶模态振型如图6至图9所示。

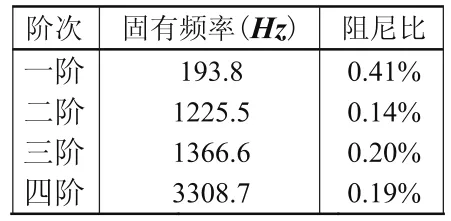
表1 吸气阀片前四阶的固有频率和阻尼比

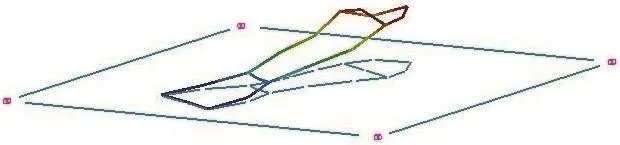
图6 实验模态分析第一阶振型图

图7 实验模态分析第二阶振型图

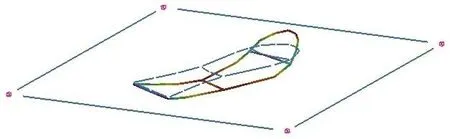
图8 实验模态分析第三阶振型图

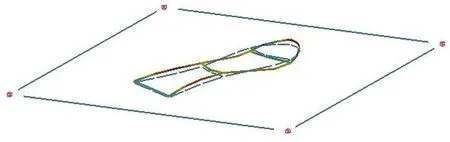
图9 实验模态分析第四阶振型图

实验模态测试结果的优劣可以通过模态置信判据(MAC)[6]来判断，模态置信判据表征的是两个模态向量的相关程度，若MAC≈1，说明这两个模态向量本质上是同一模态，若MAC≈0，意味着两个模态向量具有正交关系，是两个不同的真实物理模态。本实验前四阶的相关系数如图10所示，主对角线上是模态向量的自相关系数等于1，非主对角线上模态向量的互相关系数约等于0，这表明实验模态测试识别出的前四阶振型是正交的，模态参数识别结果是可信的。

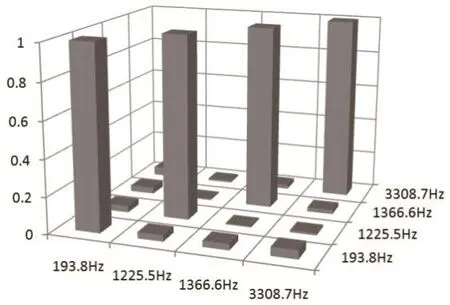
图10 前四阶固有频率的相关程度

4 理论模态计算及与实验模态分析的比较

将吸气阀片简化成一端固定的悬臂梁模型，使用Hyper Mesh划分网格，如图11所示，导入LMS Virtual.Lab软件对吸气阀片进行理论模态计算，设置吸气阀片材料为钢，弹性模量为210GPa，泊松比0.3，密度7850kg/m3，厚度0.2mm。图12至图15为吸气阀片的第一阶、第二阶、第三阶和第四阶理论模态计算振型，与实验模态分析的第一阶、第二阶、第三阶和第四阶相对应，并且振型相似。

图11 吸气阀片的简化有限元模型

图12 理论模态计算第一阶振型图

图13 理论模态计算第二阶振型图

图14 理论模态计算第三阶振型图

图15 理论模态计算第四阶振型图

分析理论模态计算的振型图可以看出，吸气阀片的第一阶振型是绕着y轴的上下往复振动，控制进气通道的开闭，这是吸气阀片工作过程中的主要振动形式，也是造成吸气阀片疲劳断裂的主要原因。吸气阀片的第二阶振型是绕着x轴的左右摆动，吸气阀片的第三阶振型是绕着y轴有一列位移峰值的上下振动，吸气阀片的第四阶振型是绕着y轴有两列位移峰值的上下振动。

表2列出了实验模态分析与理论模态计算前四阶固有频率的比较，对比表中结果可以看出：1）随着模态阶次的升高，实验模态分析和理论模态计算得到的固有频率差值逐渐变大。对于前三阶两者数值相差不超过6%，说明实验模态分析前三阶的识别精度较高；第四阶固有频率相差较大，达到了16.11%，说明实验模态分析固有频率的识别出现了较大的偏差。2）实验模态分析的前四阶固有频率均低于理论模态计算的结果。

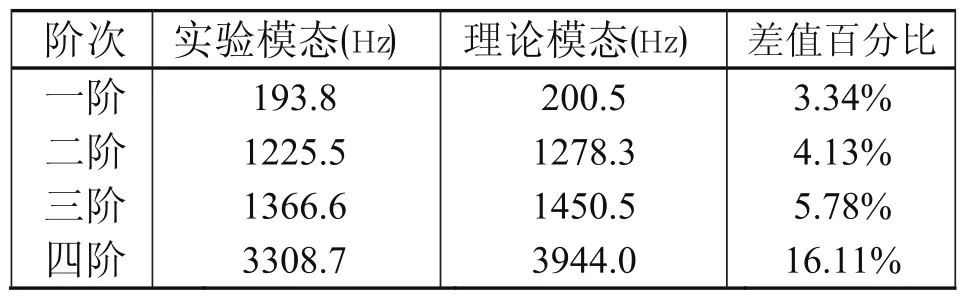
表2 吸气阀片实验模态与理论模态比较

比较分析实验模态测量结果和理论模态计算结果，我们可以发现: 1）两种方法得到的前三阶固有频率和模态振型的识别结果都比较接近，第四阶模态振型的识别是相似的，但固有频率的识别相对前三阶有较大的偏差，其原因可能是吸气阀片的装卡方式对于其高阶模态的辨识产生了较大的影响。2）当家用冰箱压缩机以3000转每分常态工作运转时，吸气阀片工作频率为50Hz，远低于吸气阀片的第一阶固有频率200Hz左右，说明实验用吸气阀片避开了共振区，其结构设计合理。

5 结论

由于压缩机吸气阀片属轻薄弹性结构，传统测量方法无法辨识出其模态参数。本文根据压缩机吸气阀片具体的结构特点，提出了一种新的实验思路，以声信号施加激励，以激光测振仪完成阀片振动响应的测量。本文设计了压缩机吸气阀片模态实验方案，完成实验系统的建立，最终实现吸气阀片振动模态参数的识别，实验模态分析结果与理论模态计算结果基本一致。因此，采用宽带噪声激励及激光拾振，实现轻薄结构体的低阶模态参数识别和振动特性分析是完全可行的。

[1] 李雷,郭其威,宋汉文.声致振动下铝板的实验模态分析与参数辨识[J].噪声与振动控制2009,6:276-282.

[2] 钟旋,昊群力,李晓东.利用激光测振改进小型扬声器系统的声学特性[J].电声器件与电路2008,32(8):22-25.

[3] 李德葆,陆秋海.实验模态分析及其应用[M].北京:科学出版社,2001:65-66.

[4] 王晶,尹亦阳,冯涛,刘斌.往复式制冷压缩机阀片振动特性测量系统设计[J].北京工商大学学报(自然科学版),2011,29(1):63-65.

[5] 苏小平,朱健.基于MSC.Nastran的轻型客车车身骨架的模态分析[J].制造业自动化,2010,32(10):141-143.

[6] 刘馥清.LMS振动/噪声测试与分析系统理论基础[M].比利时:LMS公司,2000:228.