关于图的集控制数

徐保根，罗 茜，丁宗鹏

（华东交通大学基础科学学院江西南昌330013）

1 引言及定义

文中所指的图均为无向简单图，文中未说明的符号和术语同文献[1]。

设G为一个图，对于任意v，则NG(v)表示v点在G中的邻域，dG(v)= ||NG(v)表示v点在G中的度，NG[v]=NG(v)∪{v}称为v点的闭邻域，δ和Δ分别为图G的最小度和最大度，有时，NG[v]和dG(v)分别简记为N[v]和d(v)。

设G和H为两个点不交的图，在G∪H中将G的每个顶点与H的每个顶点均邻接起来，所得的图称为G与H的联图，记为G∨H。

对于两个点不交的图G和H，则G与H的乘积图记为G×H，其定义为

E

设G为一个图，D⊆V(G)，如果对于V(G)D中的每个顶点v，存在u∈D，使得u与v在G中邻接，则称D为G的一个控制集，容量最小的控制集包含的点数称为G的控制数，记为γ(G)。

图的控制理论是图论中的重要分支，美国图论学者W.T.Haynes等[2]在1998年出版的专著较为系统地综述了这一领域的一些主要研究成果。在1977年，E.J.Cockayne和S.T.Hedetniemi[3]引入了图的集控制概念并研究图的集控制数，B.Zelinka[4-5]在图的集控制方面做了大量工作，得出了集控制数与图的其它参数之间的关系，如集控制数与线性点荫度的关系[4]等。

定义1[3]设G是一个图，如果V(G)能划分为t个两两不交的控制集Di(i=1，2，...，t)，则称G有t-控制集划分。图G的集控制数记为d(G)，其定义为:d(G)=max｛t|存在G的t-控制集划分｝。

对于任何图G，由于D=V(G)本身就是G的一个控制集，故d(G)总是存在的，并且不难证明下面的结论。

引理1[6]对任意图G，均有d(G)≤1+δ(G)。且v1邻接v2，或者v1=v2且u1邻接u2｝。

在本文中，我们主要研究乘积图与联图的集控制问题，给出这两种图集控制数的界限，并确定了一些特殊性图的集控制数，这包括Km×Kn和Pm×Pn等。

2 主要结果及其证明

首先给出两个图的乘积图与联图的集控制数的界限，然后确定Km×Kn和Pm×Pn的集控制数。定理1 对于任意n阶图G和m阶图H，均有

并且此上界和下界均是可达的。

1）先证max{n，m} ≥d(G×H)，不妨设n≥m，即证n≥t。

（反证）假若n≤t-1，由定义知:V(G×H)能划分为t个两两不交的控制集Di(i=1，2，…，t)，即

V(G×H)=D1∪D2∪…∪Dt，并且Di∩Dj=∅ (1≤i≠j≤t)，注意到，故上述划分中存在一个Dk，使得

∀u∈V1，v∈V2，由乘积图的定义知:图G×H中的点(u，v)不与Dk中的任何点相邻，这与Dk为G×H的控制集矛盾，从而n≥t。

2）下面证明d(G×H)≥max{d(G)，d(H)} 。

记d(G)=p，d(H)=q，不妨设p≥q，将V(G)划分为p个两两不交的控制集Ai(i=1，2，…，p)，即V(G)=A1∪A2∪…∪Ap，并且Ai∩Aj=∅(1≤i≠j≤p)。

现将V(G×H)分成p个子集如下

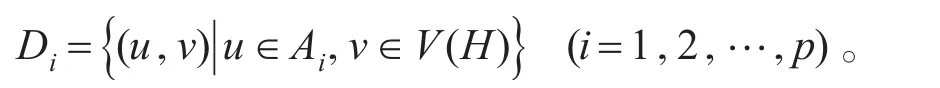
由于每个Ai均是G的控制集，故每个Di均是G×H的控制集，即d(G×H)≥p。

特殊地，当G=Kn为n阶完全图，且n≥m时，定理给出的上、下界限均可达。至此，定理1证毕。

注意到d(Kn)=n，故由上述定理1可直接得到下面两个推论。

推论1 设n和m为整数，且n≥m，则对任意m阶图H，均有d(Kn×H)=n。

推论2 对于任意正整数m和n，均有d(Km×Kn)=max{m，n} 。

定理2 对于任意n阶图G和m阶图H，均有

并且此上界和下界均是可达的。

证明 不妨设n≥m。记先证d(G∨H)≥m。只需将V(G∨H)划分为m个控制集即可，事实上，可令

可见上述每个Di(i=1，2，…，m)均为G∨H的控制集，即d(G∨H)≥m。

下面证明d(G∨H)≤min{m+d(G)，n+d(H)} 。

由对称性，只需证明d(G∨H)≤m+d(G)即可。记d(G∨H)=t，d(G)=r。

（反证）假若t≥m+r+1，由定义知V(G∨H)能划分为t个图G∨H的控制集，即

V(G∨H)=D1∪D2∪…∪Dt，且Di∩Dj=∅(1≤i≠j≤t)。注意到 |V(H)|=m，t≥m+r+1，故这些控制集中至少有r+1个控制集均不包含图H中的点，这r+1个控制集记为Di1，Di2，…，Di(r+1)，它们均不包含图H中的点，且均为G∨H的控制集，故每个Dij(j=1，2，…，r+1)均为图G的控制集，注意到其为两两不交的，从而d(G)≥r+1，矛盾。定理2证毕。

定理3 对于任意正整数m≥3和n≥2，均有d(Pm×Pn)=3

证明 令G=Pm×Pn，可见δ(G)=2，由引理1知d(G)≤3。

E下面只需将V(G)划分为3个控制集V(G)=D1∪D2∪D3。

情况1 当n≡0(m od3) 时，令

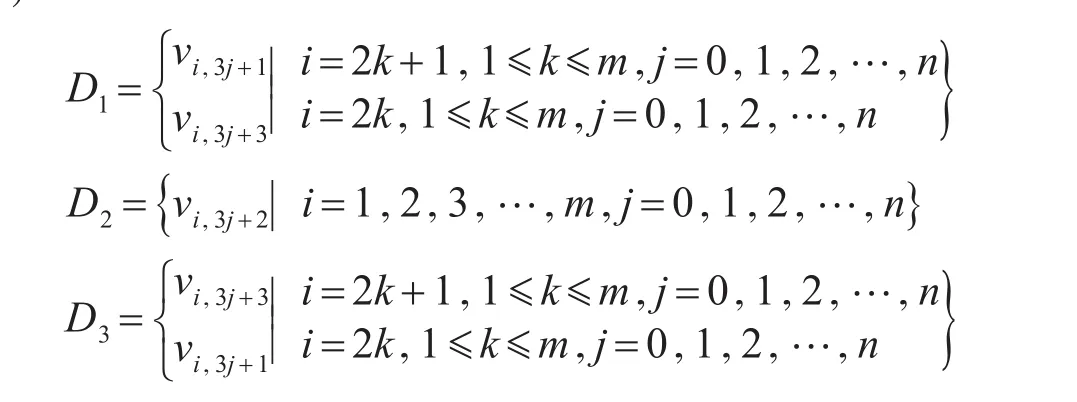
情况2 当n≡1(m od3) 时，令V=V1∪V2，其中，V1中的点可以仿照情况1进行划分，我们只需对V2中的点进行划分即可。那么

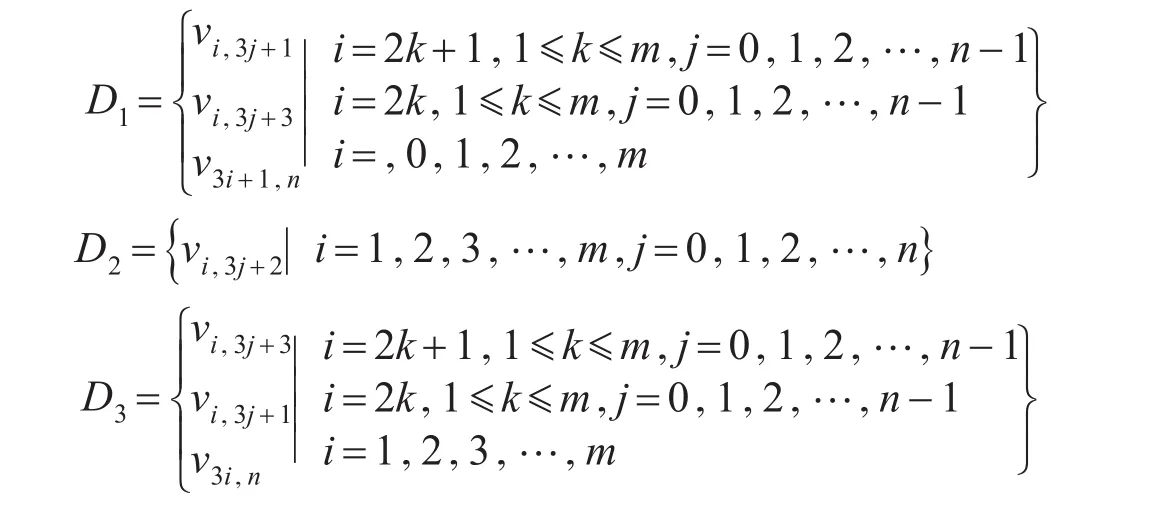
情况3 当n≡2(m od3) 时，令V=V1∪V2，

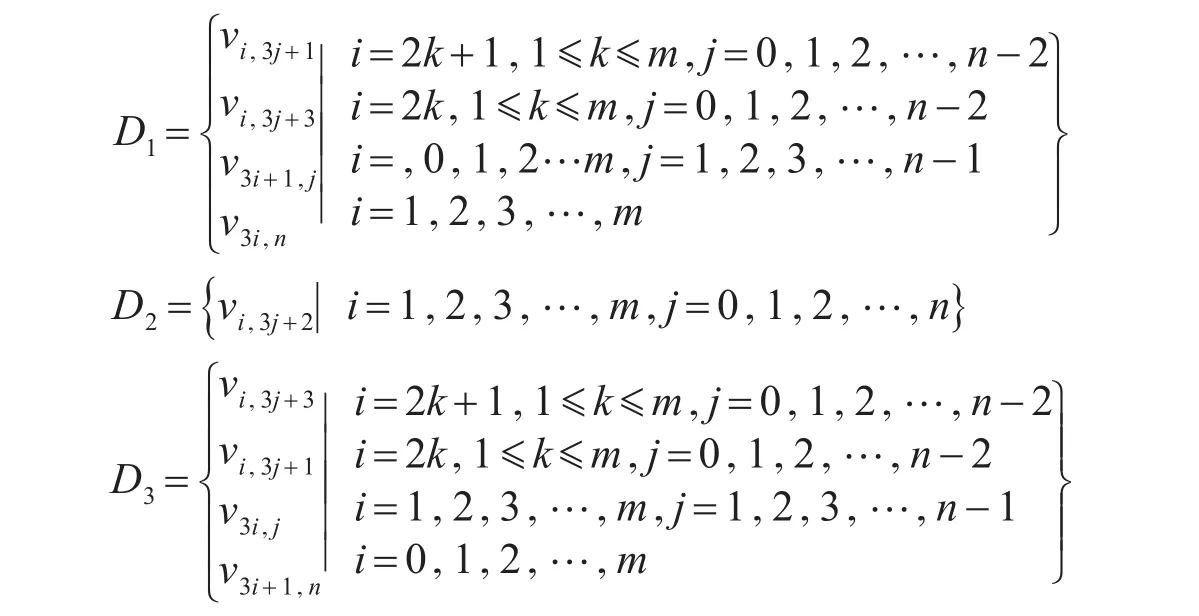
综上所述，V(G)能划分为3个控制集，定理3证毕。

[1]BOND JA，MURTYV S R.Graph theory with applications[M].Amsterdam:Elsevier，1976:247-250.

[2]HAYNES T W，HEDETNIEMI S T，SLATER P J.Domination in graphs[M].New York:Marcel Dekker INC，1998:150-155.

[3] COCKAYNE E J，HEDETNIEMI S T.Towards a theory of domination in graphs[J].Networks，1977（7）:247-261.

[4]ZELINKAB.Domatic number and linear arboricity of cacti[J].Slovaca Math，1986（36）:41-54.

[5] ZELINKAB.Domatic number and degrees of vertices of a graph[J].Slovaca Math，1989（39）:7-11.

[6]徐保根.图的控制理论[M].北京:科学出版社，2008:103-113.