大型高压干式潜水电机定子三维温度场有限元分析
鲍晓华,吕 强,王瑞男,朱庆龙,刘 冰
(1. 合肥工业大学电气与自动化工程学院,合肥 230009;2. 合肥三益江海泵业有限公司,合肥 231131)
引言
大型高压干式潜水电机主要用于大型水利工程、城市给水排水系统以及矿井排水、抢险救灾等场合。随着我国潜水电机制造业的发展,潜水电机的单机容量不断增长,在潜水电机的设计中越来越多的采用高电磁负荷和热负荷的材料,电机运行时产生的单位体积损耗不断增长,这将会导致潜水电机温升过高或局部温升过高,不仅会降低电机的使用寿命,影响电机的出力,效率等性能和经济技术指标,还会引起结构部件严重变形,危及电机运行安全。大型潜水电机常年工作于深水,检修起来十分困难,这就要求潜水电机运行的稳定性极高,因此对潜水电机运行时三维温度场的分析计算显得日益重要。正确计算与研究潜水电机各部件温升情况,不仅可以优化电机设计,还为今后电机高效、安全运行奠定了坚实的基础。近年来随着计算机数字技术的不断发展,国内外的学者对于大型发电机的温度场的研究做了很多工作,但对于潜水电机三维温度场的研究工作还不多,这方面的文献还不常见。
传统的电机温度场计算主要采用简化公式法,等效热路法,等效热网络法[1,2]等,这些方法能够准确描述电机的实际模型,物理意义明确,计算量相对较小,曾经得到广泛应用,然而该方法主要是近似估算电机定子的平均温升,无法得出某一具体点的温度值,不能很好地确定定子各部件温度场的实际分布情况。最新的电机温度场计算方法主要有有限差分法,有限元法[3]等,而有限差分法采用的是交直网格,比较适合求解边界比较规则的温度场问题,比较难适应电机求解区域形状的任意性,因此有限元法成为求解潜水电机定子三维温度场的必然选择。
本文根据传热学理论,建立了大型潜水电机定子三维温度场的数学模型,给出了潜水电机导热系数及散热系数的计算方法。应用有限元法对潜水电机定子三维温度场进行分析计算,并将结果与实际测量值进行比较,验证了所述方法的正确性和实用性。最后,分析了潜水电机采用不同绝缘等级时对电机定子温度场的影响,得出了一些十分有益的结论,对潜水电机设计及其优化工作具有重要的指导意义。
1 潜水电机定子三维温度场理论计算
1.1 计算模型
本文中潜水电机为全封闭式空气内冷、机壳水外冷电机,电机内部采用轴流风扇和离心风扇相结合通风方式。在整个通风系统中,风路共分为两个回路:一路是从轴流风扇进风,经定转子气隙,离心风扇,吹拂定子上端部绕组后,热风经散热管冷却,进而吹拂定子下端部绕组,再次进入轴流风扇循环;另一路是从轴流风扇进风,经转子内通风道,离心风扇,吹拂定子上端部绕组后,热风经散热管冷却,进而吹拂定子下端部绕组,再次进入轴流风扇循环,如图1所示。
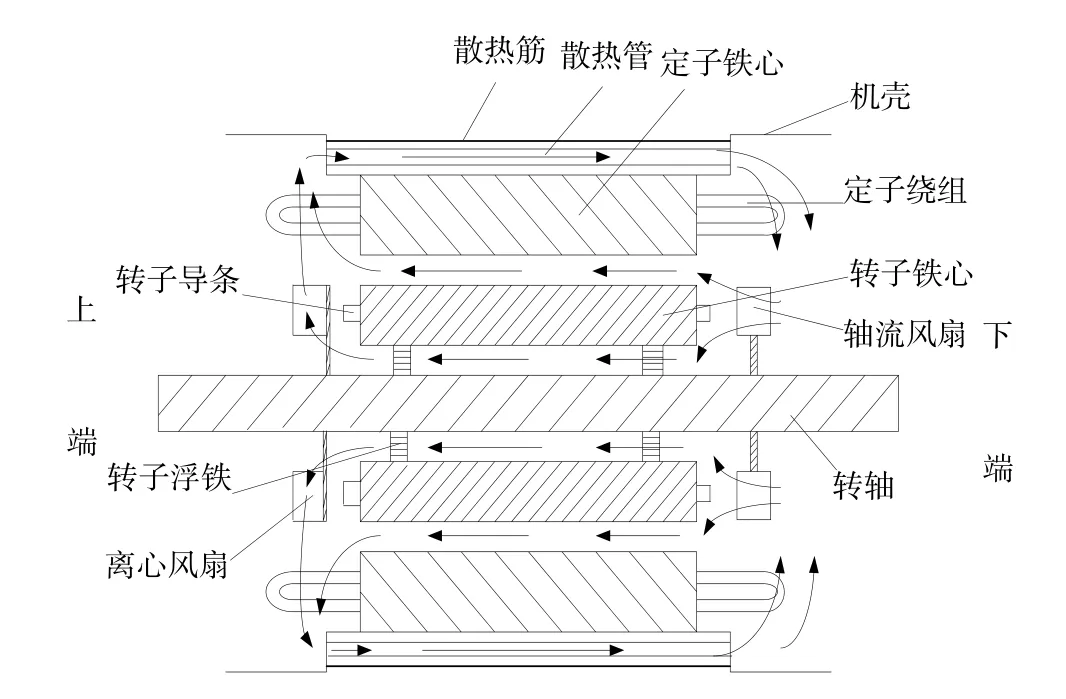
图1 潜水电机风路
1.2 基本假设
潜水电机的定子结构复杂,计算区域内包括很多材质:定子铁心、铜导线、槽楔、绝缘、漆膜、空气隙等,而且其中定子铁心的导热系数呈各向异性。为了计算方便,做如下假设[6]:
1)为了计算上的方便,取一个半齿槽作为计算区域。
2)风路中空气中的雷诺数Re远大于2300,空气流动处于紊流状态,因此采用紊流模型对转子温度场进行求解。
3)计算定子铜耗时,假设涡流效应对每根导线的影响基本相同,即取其平均值。
4)考虑到潜水电机气隙较大且空气层导热系数极小的缘故,认为定转子之间没有热交换。
5)认为各槽导线均匀排列。
6)由于周向的对称性,认为槽中心面与齿中心面都是绝热面。
1.3 计算模型
根据以上假设,对潜水电机定子采用等效体积法进行建模,其中一个半齿槽计算模型如图2所示。
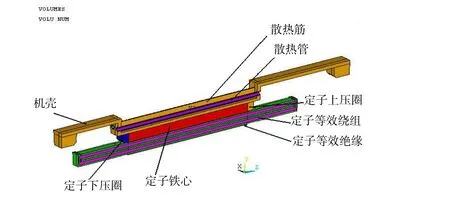
图2 定子计算模型
1.4 三维稳态热传导方程及其等价变分
由传热学基础知道,对于电机稳态导热过程,温度不随时间变化,某一计算区域内的稳态温度场求解问题可以归结为如下的边值问题[4,5]:
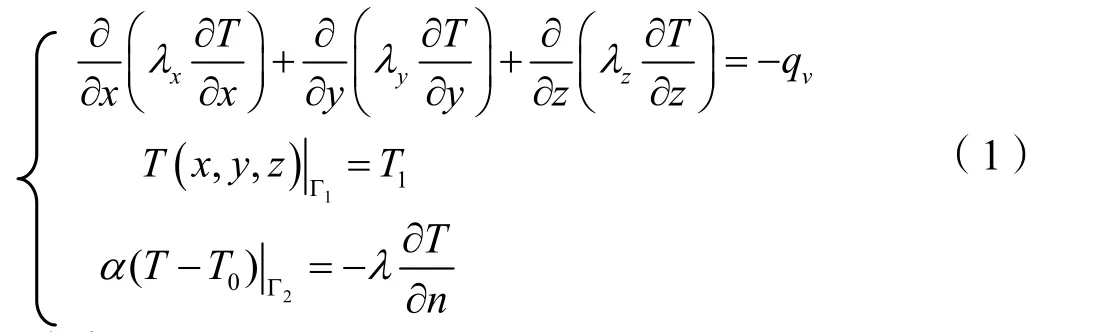
式中:
、yλ、zλ——沿x、y、z方向的导热系数,(W/m·k);
T1——边界面Γ1上的给定温度;
n——边界面(Γ1,Γ2)上的法向矢量;
α——Γ2表面的散热系数;
T0——Γ2周围介质的温度。
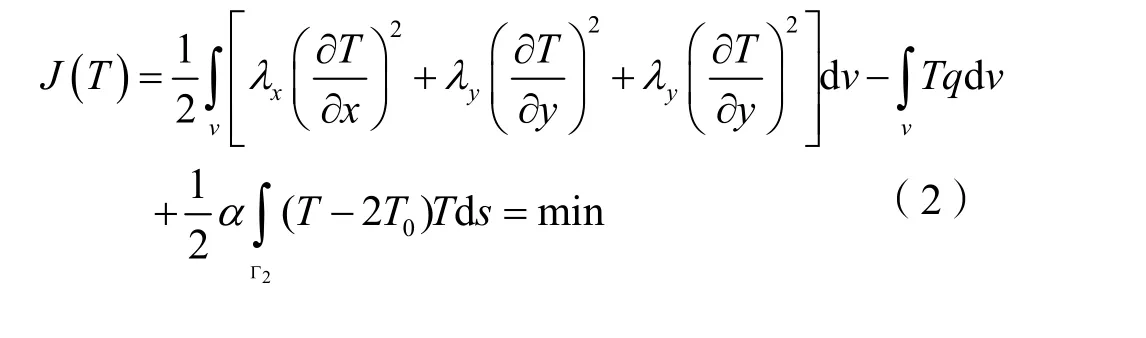
相应于式(4)的等价泛函为
对等价泛函进行变分计算时,把上式定义到计算单元的区域范围内,则上式可以改写为
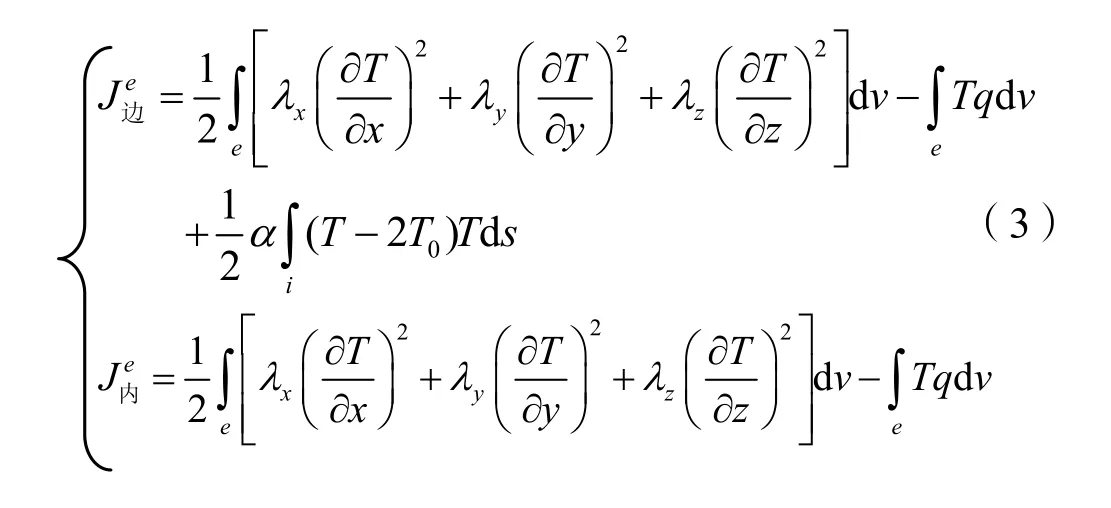
式中,符号e表示单元的意思,这里只有边界单元的i边才有边界,内部单元没有边界。又由于单元 e内的温度场已离散成只与T1,T2,T3,T4,T5和T6六个节点温度有关的插值函数,这样就将 J(T)的变分问题转化为多元函数求极值问题,即
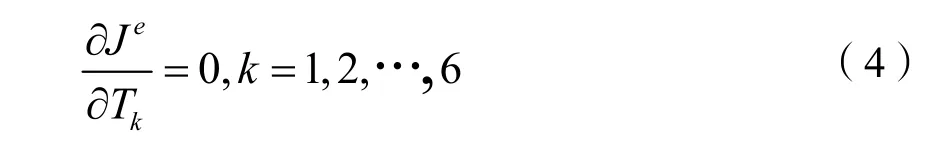
由此可得

式中,{T}为求解域内全部节点温度所形成的温度列阵;系数矩阵[K]为温度刚度矩阵;{P}称为总体右端列向量。
求解该方程组,即可求得各个节点的温度值。
2 绝缘导热系数、表面散热系数及损耗的确定
2.1 绝缘导热系数的确定
电机中的绝缘材料常用多种不同材料组合而成,其导热系数理论上可由下式[2]求得:
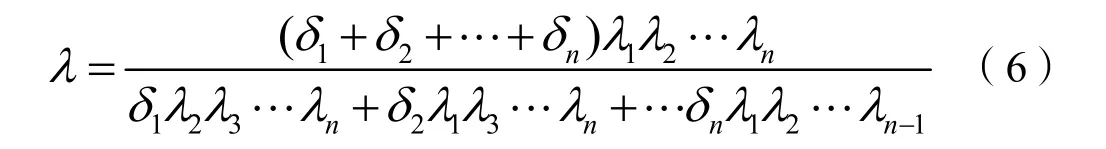
式中:1δ2δ…nδ——不同绝缘材料的厚度;
λ——等效绝缘的合成导热系数。
但实际上材料层间难免留有空隙,而且各种材料也并非完全均质,因此,应用时还是根据实验资料较为可靠。大型电机通常取A级绝缘导热系数Aλ=0.1W/(m·K);B级绝缘导热系数Bλ=0.16 W/(m·K);F级绝缘导热系数Fλ=0.26 (m·K)。上述数值实际上包含了绝缘层间的工艺性气隙。潜水电机绕组经烘干、压制、浸漆后,绝缘层间工艺性气隙很小,试样测得的结果要比上述数值大一些。
2.2 表面散热系数的确定
2.2.1 电机内部各表面的散热系数
由于空气在潜水电机风路中是受迫流动,且风路很不规则,因此流动状态大多数情况下是紊流。流体在风道中流动状态为紊流时(Re>3×104),热交换的标准等式可以描述为[7]:
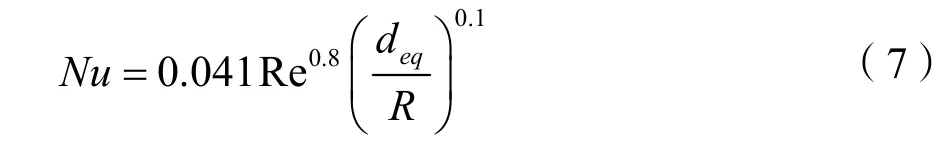
式中:Nu——努谢尔特准数;Re——雷诺兹系数;——通风道的等效直径;R——散热表面距旋转中心的半径。
而在紊流情况下,流体运动相似性准则可表达如下:

式中:u——通风道中空气的流动速度;
v——冷却介质的粘性系数;
λ——流体导热系数;
α——表面散热系数。
联立(11)、(12)、(13)三式可得表面散热系数:

Nu——努谢尔特准数;
u——风道冷却介质的速度;
v——冷却介质粘性系数;
deq——风道的等效直径。
空气冷却时,导线表面的散热系数,以及电机其他部分的表面的散热系数都可以由上式计算。
2.2.2 机壳、散热管及散热筋表面的散热系数
潜水电机工作在水中,电机外表面为水冷。当水在电机表面流动为层流时

即

当水在电机表面流动为紊流时

式中:Pr——冷却介质的普朗特准数;
w——水在电机表面的流速;
α——热扩散率;
lf——水的导热系数;
L——水沿机壳壁的流动长度。
2.3 损耗的确定
本文选用的潜水电机额定功率为800kW,额定电压为10kV,额定电流为55.6A,额定转速为975r/min。定子求解域内,定子绕组为主要的发热部件,此外定子还有铁耗,附加损耗等。因此,定子绕组及定子铁心所在的单元都具有损耗热源。各项损耗值分别由相关分析和试验方法得到。定子三维温度场计算时分别将电机各部分损耗热源密度施加到电机的有限元计算模型中,作为计算时的热源。
3 计算结果与实验结果对比分析
3.1 额定工况下定子三维温度场
用上述方法对合肥三益江海泵业有限公司(原合肥电机厂)YQGN850型高压干式潜水电机在额定工况下定子的三维温度场进行了计算,得到定子铁心和绕组的三维温度分布,如图3和图4所示。
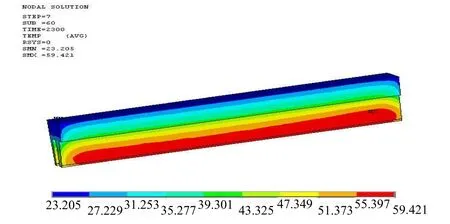
图3 定子铁心三维温度分布图

图4 定子绕组三维温度分布图
由图3所示可以看出,定子铁心最高温度出现在定子齿中心处,为55.397℃,最低温度出现在定子轭部,为23.205℃。定子铁心上部温度高于下部,这是由于电机风路中,由散热管吹出的冷风首先吹拂定子铁心下部,最后吹拂上部铁心所致;潜水电机定子铁心径向温度梯度很大,这是由于机壳水外冷时,散热系数大,能迅速带走大量的热量。
由图4可知,定子绕组最高温度出现在绕组上端部,为101.001℃;最低温度出现在上层绕组中心处,为72.919℃。上层绕组比下层绕组平均高出8℃左右,这是由于定子绕组热量主要经定子铁心传到机壳后散发出去,而定子铁心上部比下部温度低很多所致。
3.2 计算结果与实验值对比分析
样机定子绕组、铁心温度值的计算结果与试验结果的对比如表1所示。

表1 计算结果与实测值对照
由上表可以看出,计算结果与实测值在一定的误差允许范围之内,因此可以证明潜水电机定子三维温度场计算模型的正确性及计算结果的准确性。
4 采用不同绝缘等级对潜水电机定子温度场的影响
由图 5(a)、(b)、(c)可以看出,采用不同绝缘等级对潜水电机定子绕组温升影响比较明显,但对电机定子其他部分温升影响不大。因此,设计潜水电机时可以利用提高绝缘等级来降低定子绕组温升,从而达到提高电机电磁负荷的效果。
5 小结
通过对潜水电机定子三维温度场有限元计算,可以得到以下结论:
(1)潜水电机定子绕组温升分布呈现奇异性,最高温度出现在绕组两端,最低温度出现在定子绕组中部,嵌在定子铁心内的部分。
(2)提高绝缘等级可以有效降低潜水电机定子绕组温升。

图5 不同绝缘等级时定子三维温度场分布图
(3)三维温度场有限元计算为改善电机温升分布提供了参考依据,为电机设计和机械设计以及电机安装角度降低电机温升提供了重要计算手段。
[1]方日杰, 赖烈恩, 蒋俊杰. 用热网络法计算大型水轮发电机定子温度场[J]. 大电机技术, 1989(1),25-29.
[2]魏永田, 孟大伟. 电机内热交换[M].北京: 机械工业出版社, 1998.
[3]D. Aldo, C. Andre, L. Maria, et al. A Simplified Thermal Model for Variable-speed Self-cooled Industrial Induction Motor[J]. IEEE Transactions Industry Applications. 2003, 39(4): 945-952.
[4]孔祥谦.有限单元法在传热学中的应用[M].北京:科学出版社, 1981.
[5]A. Boglietti, A. Cavagnino and D. A. Staton, TEFC induction motors thermal models:A parameter sensitivity analysis , IEEE Transactions on Industry Applications, 2005, vol. 41, 756-763.
[6]李伟力, 周封, 侯云鹏等. 基于流体相似理论和三维有限元法计算大中型异步电动机的定子三维温度场[J]. 中国电机工程学报, 2000, 20(5),74-78.
[7]A.N.鲍里先科.电机中的空气动力学与热传递[M].北京: 机械工业出版社, 1985.

