CORDIC 算法的一种补码实现结构设计✴

孙学

（中国西南电子技术研究所，成都610036）

CORDIC 算法的一种补码实现结构设计✴

孙学

（中国西南电子技术研究所，成都610036）

根据CORDIC算法原理，分析了该算法角度旋转范围缺陷，提出360°覆盖的角度旋转算法结构；推导出利用补码实现CORDIC算法的迭代运算单元结构，并根据该补码运算原理设计了CORDIC补码迭代运算单元和方向向量发生器的实现结构。

坐标旋转数字计算机；方向向量；补码电路

1 引 言

CORDIC是Coordinate Rotation Digital Computer（坐标旋转数字计算机）的首字母缩写，该数值逼近迭代算法由J.E.Volder于1959年提出［1］。其主要优点在于用简单的移位和加减运算取代查三角函数表和乘法运算，实现二维矢量的旋转运算，特别适合于大规模集成电路的实现。另外，CORDIC算法用于估算平方根、正余弦、指对数等初等函数的特点［2］，被广泛应用于导航解算、频偏估计、调制解调和频率合成等矢量运算场合［3-5］。

本文第2节基于CORDIC算法原理分析了该算法实现角度旋转存在覆盖范围缺陷，提出一种360°角度覆盖的CORDIC旋转算法结构。第3节基于该算法结构，创新性地推导出CORDIC迭代运算单元的一种补码实现结构，是本文的描述重点。

2 CORDIC算法

2.1 CORDIC算法原理［1］

通过旋转一系列小角度的以偏摆逼近所需的角度、开方以及反三角函数等复杂运算逻辑，复数P=

x+j y旋转θ角度得到Q的过程就是复数P与复指数ejθ进行复乘得到Q的过程。如果旋转角度θ可以分解成N个小角度φi之和，那么旋转角度θ就等效于旋转这N个小角度φi。

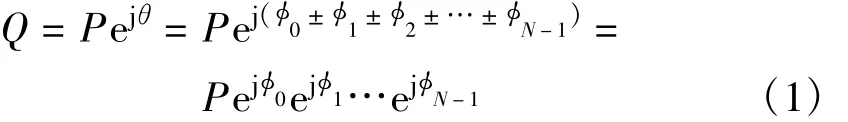
其角度θ分解方法为

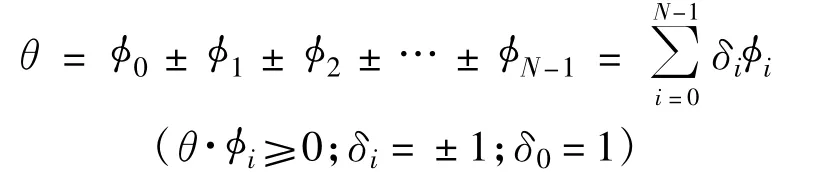
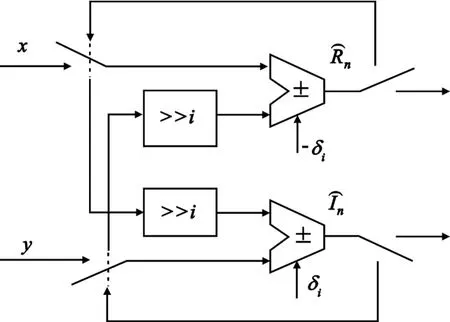
图1 CORDIC算法迭代结构框图Fig.1 Circuit of original form CORDIC iteration operator

2.2 角度旋转范围缺陷及补偿设计

由于φi=arctg 2-i在i=0，1，…，N-1时小于等于π／4且单调递减，（N趋于无穷大）收敛，下面证明θ收敛范围。

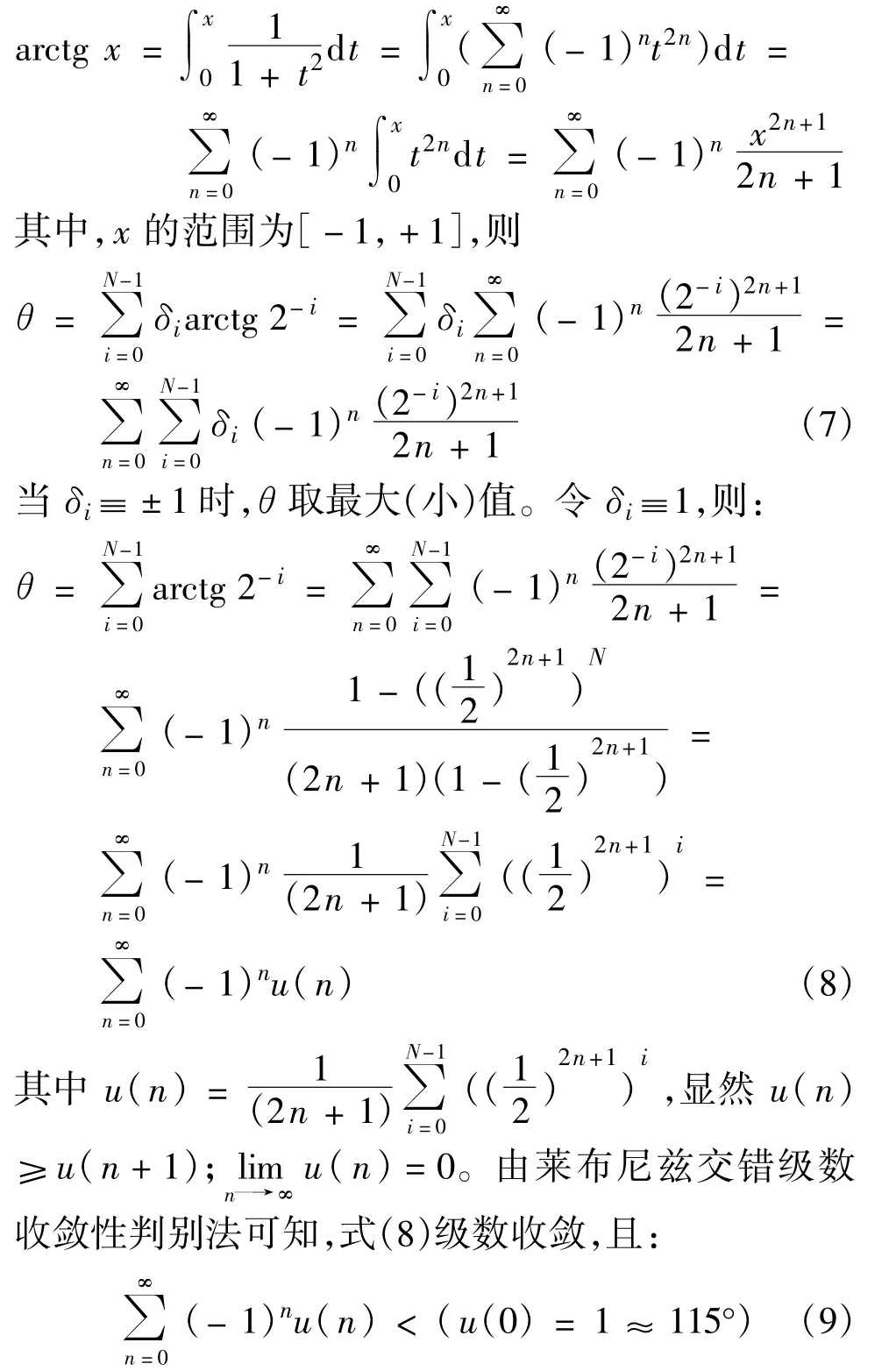
因此，用CORDIC算法实现数据的相位旋转时，需要扩大CORDIC算法的角度旋转范围，从（-99.883°，+99.883°）扩展到［-180°，180°］，在实际工程应用中，通常把［-180°，180°］表达为［0°，360°］或［-360°，0°］的角度旋转，设计如下。

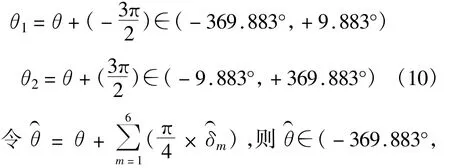
+369.883°），覆盖360°的角度旋转范围。取N=16时，则

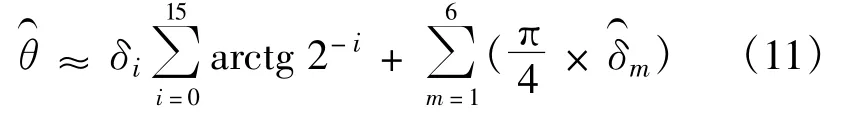
该方法是在CORDIC移位序列前加上6个φi= arctg2-i（i=0）迭代，在270°范围内实现旋转步进为粗定位，在此基础上通过不断减小角度旋转步进摇摆逼的精确定位。式（11）设计旋转角度粗定位方法，导致复数P每旋转45°后幅度放大1.414倍，使得式（5）中校正因子K放大8倍。在实现式（11）的CORDIC处理器时，为了减小旋转过程中对复数P实部和虚部表达范围的影响，在这6个迭代的每两级旋转后，实部和虚部各右移一位，缩小一倍以免数值溢出。

3 C ORDIC补码实现结构设计

3.1 CORDIC的原码实现原理

根据CORDIC算法迭代结构框图，设计其原码实现结构，如图2所示。

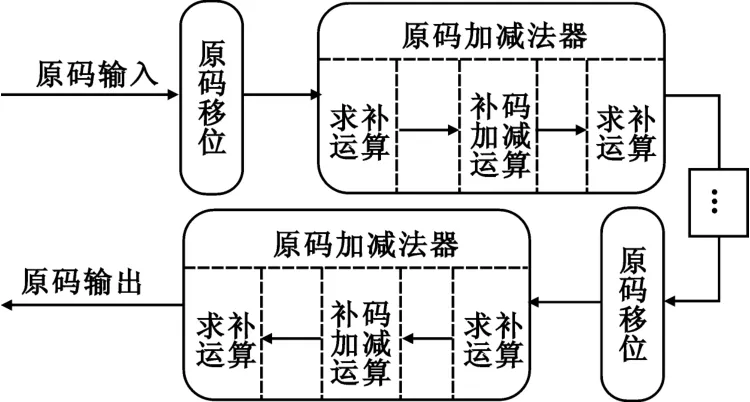
图2 CORDIC的原码实现原理Fig.2PrincipleoforiginalformCORDIC

CORDIC算法的原码实现结构优点在于原码移位简单，缺点在于补码方式实现二进制加减法前后，都需要进行求补运算，原码实现结构中每一级迭代运算都需要4个补码器并导致2级求补运算时延。采用流水线结构实现式（11）的CORDIC需要88个补码器，导致44级求补运算时延，不但会导致器件资源的大量消耗，在高实时矢量运算场合还将带来严重的时延问题。为此，本文设计了一种补码实现结构的CORDIC处理器，能够有效解决以上技术问题。

3.2 CORDIC的补码实现原理

补码实现CORDIC处理器的基本思想是：原码数据在输入CORDIC运算器之前进行补码运算，在CORDIC运算器的运算过程中全部采用补码运算，CORDIC运算结果进行求补运算，输出原码数据，如图3所示。

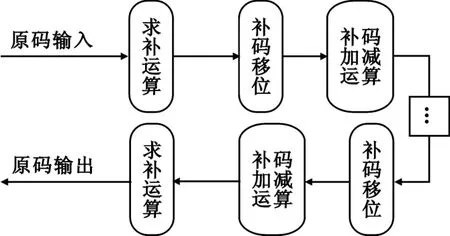
图3 CORDIC的补码实现原理Fig.3PrincipleofcomplementaryformCORDIC

该实现方法的关键在于补码移位算法和CORDIC补码迭代单元设计。

3.3 补码移位器设计

假设输入的整数X的原码数据为

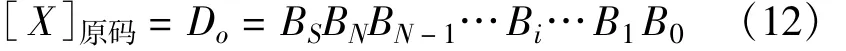
其中，BS为符号位，“1”表示负数，“0”表示正数，0≤i≤N表示数据的数值位。需要说明的是：十进制0的原码表示为符号位BS=0，即只有正“零”，不允许负“零”的出现。

定义负整数X的反码为

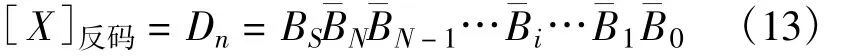
即符号位不变，数值位进行取反运算；正整数X的反码为它的原码本身。

定义数据的补码为

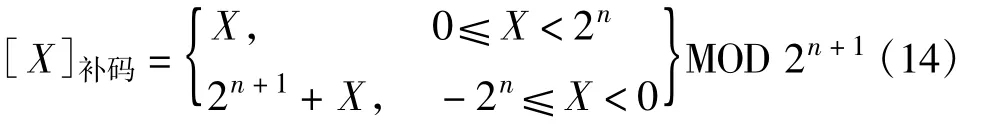
式中，n为二进制整数数值位的位数。由定义可以推出，补码的求补运算结果为数据的原码。为了得到一个数的补码表示，当然可以通过补码的定义求得，但更简便的办法如下。

（1）BS=0时，正整数数据的补码等于它的原码本身：

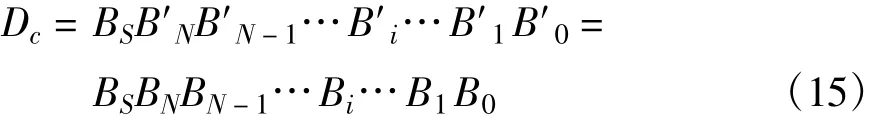
（2）BS=1时，负整数数据的补码等于它的反码加“1”：

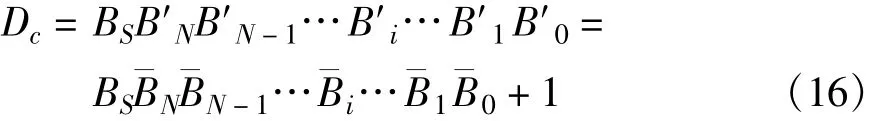
由于正数的补码等于它的原码本身，所以正数的补码移位和它的原码移位规律相同，真值除以2i的补码实现和真值除以2i的原码实现方式相同，不用讨论，现在要研究的是负数的补码实现真值除以2i运算规律。负数的原码表示为

¯Bi-1or¯Bi-2or…or¯B1or¯B0=0时，则D2+1=D5，即B′i-1or B′i-2or…or B′1or B′0=1时，补码右移i位的结果再加上“1”才实现真值除以2i的功能。

综上所述，补码实现真值除以2i功能的实现主要是靠补码右移i位来实现，其实现方法是：

（1）BS=0，则真值除以2i的补码实现和真值除以2i的原码实现方式相同，都是直接右移i位，高位补“0”来实现真值除以2i；

（2）BS=1，如果B′i-1or B′i-2or…or B′1or B′0=1为假，真值除以2i的补码实现方式是右移i位，高位补“1”；如果B′i-1or B′i-2or…or B′1or B′0=1为真，真值除以2i的补码实现方式是右移i位，高位补“1”的基础上再加上“1”。

综合以上两种方法得到二进制数的真值除以2i的补码表达式为

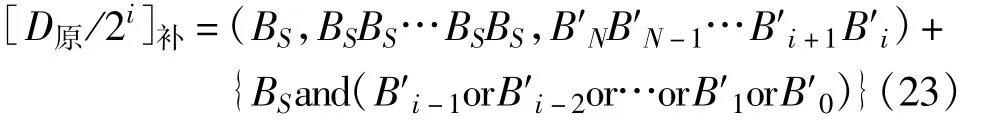
式（23）的实现结构如图4所示。

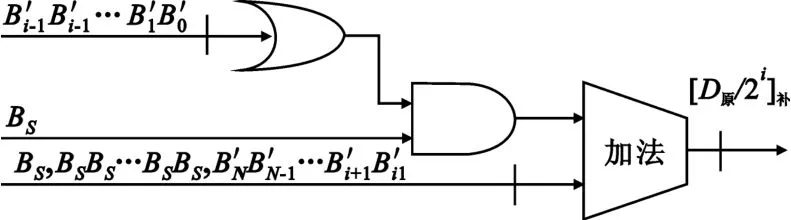
图4 补码移位器结构设计Fig.4 Complementary form shifting

3.4 方向向量发生器设计

设旋转因子WkN相位旋转通过N次CORDIC迭代实现，则方向向量δi集合中的元素个数为N。实现该算法的一种运算结构是预先计算好δi后存储在ROM中，这种方案仅适合固定角度的旋转运算，不可能为每一种旋转角度取值进行预先的旋转向量计算。为此，本文提出方向向量δi实时发生器的设计方案解决了该问题。

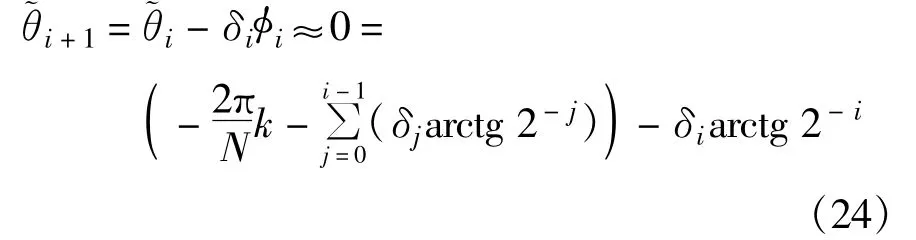
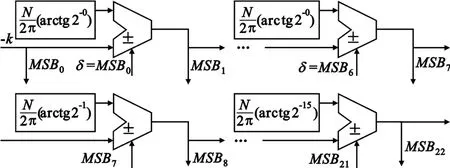
图5 方向向量δi发生器Fig.5 Direction vector generator

3.5 CORDIC补码迭代单元设计

根据［x±y］补码=［x］补码±［y］补码，也就是说，x±y真值的补码等于［x］补码和［y］补码二进制加减法的运算结果。结合图3的CORDIC补码实现原理，使用补码加减法器实现CORDIC迭代运算过程中的加减法，设计式（4）的补码迭代运算单元。

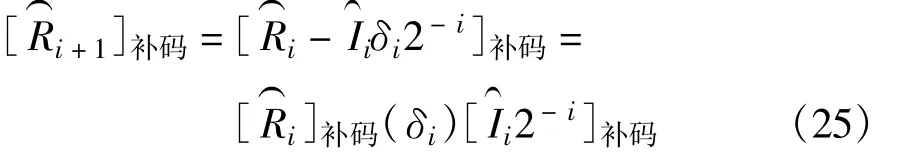
其中，当δi=+1时，（δi）表示减法运算；当δi=-1时，（δi）表示加法运算。代入式（23），则：

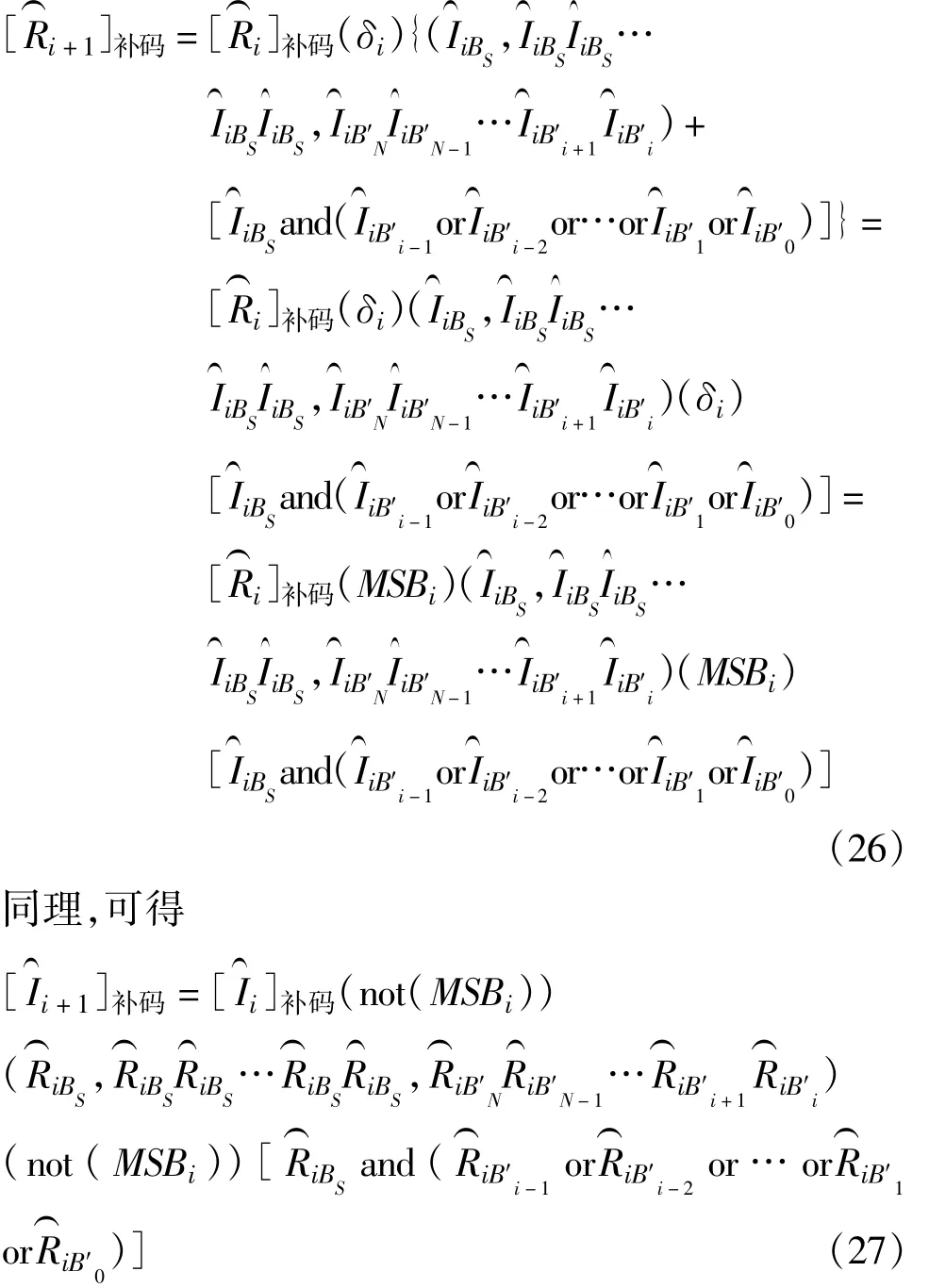
因此，设计CORDIC补码迭代运算单元的实现结构如图6所示。

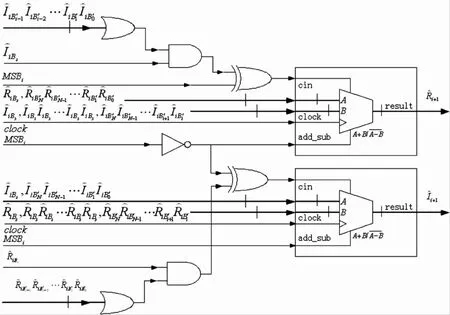
图6 CORDIC补码运算单元实现结构Fig.6 CORDIC iteration operator based on complementary form shifting

4 小 结

CORDIC作为一种计算向量旋转的迭代算法，算法结构简单，易于并行化处理和VLSI实现，因而在实时信号处理方面有广泛的应用前景。本文提出一种补码实现CORDIC的流水线电路结构，与其源码实现结构比较，省去每级迭代运算单元的2次求补运算过程，运算时延减少了一半，有效缓解了CORDIC算法固有收敛速度与高实时矢量运算场合低时延要求的矛盾。该设计可以作为CORDIC算法实现的一种技术参考。

［1］Volder J E.The CORDIC Trigonometric Computing Technique［J］.IRE Transactions on Electronic Computers，1959，8（3）：330-334.

［2］Walther JS.A Unified Algorithm for Elementary Functions［C］／／Proceedings of American Federation of Information Processing Societies Spring Joint Computer Conference.New York：ACM，1971：379-385.

［3］Stephan W Mondwurf.Benefits of the CORDIC Algorithm in a Versatile Cofdm Modulator／Demodulator Design［C］／／Proceedingsof the Fourth IEEE International Caracas Conference on Devices，Circuits and Systems.Aruba：IEEE，2002：117-119.

［4］Despain A M.Fourier Transform Computers Using CORDIC Iterations［J］.IEEE Transactions on Computers，1993，23（10）：993-1001.

［5］Hu Y H.The quantization effects of the CORDIC algorithm［J］.IEEE Transactions on Signal Processing，1992，40（4）：705-707.

Circuit Design of Com plementary Form CORDIC Algorithm

SUN Xue
（Southwest China Institute of Electronic Technology，Chengdu 610036，China）

This paper analyses the limitation of angle rotation range in CORDIC（Coordinate Rotation Digital Computer）algorithm according to its principle，and proposes an angle rotation structure covering 360 degree，and designs the pipeline circuit architecture of direction vector generator.The mathematical deduction of CORDIC operator is given based on complementary form shifting and the circuit design of CORDIC iterations.

CORDIC；direction vector；complementary circuit

the M.S.degree from Chongqing University in 2004.He is now an engineer.His research concerns switch fabric，distributed computing and array computing.

1001-893X（2011）08-0085-05

2011-03-01；

2011-06-10

TN919.3；TP301

A

10.3969／j.issn.1001-893x.2011.08.018

孙学（1978—），男，重庆合川人，2004年于重庆大学获硕士学位，现为工程师，主要研究方向为交换式总线、分布式计算和阵列计算技术。

Email：sun8xue＠163.com

SUN Xue was born in Hechuan，Chongqing，in 1978.He