改进的量子遗传算法及其在WMSN覆盖优化中的应用*

严 英，郭 剑，孙力娟

（1.南京邮电大学计算机学院 南京 210046；2.南京邮电大学计算机技术研究所 南京 210003）

1 引言

遗传算法 （genetic algorithm，GA）是进化计算的一个分支，也是软计算的关键技术之一。它本质上是一种随机搜索算法，在数据挖掘、机器学习、图像处理、网络优化等领域获得了广泛的应用[1～2]。但是应用GA算法来解决实际问题时，人们也遇到了不少困难。最常见的问题就是遗传算法的收敛速度缓慢，且常常收敛于局部最优解。为了解决这个问题，研究者也提出了不少改进[3～4]。Han等人[5]首次将量子计算的相关概念引入到遗传算法的框架中，提出了量子遗传算法（quantum genetic algorithm，QGA）[6，7]。QGA算法对GA算法的编码方式与演化操作都进行了改进，使得算法的收敛速度大大加快，但算法收敛到局部最优解的问题仍然没有很好地解决。

本文对QGA算法进行了研究，针对QGA算法早熟的问题，从算法机制的角度进行了分析。QGA算法每次迭代时，以一个最优染色体来指导群体的进化，破坏了染色体的多样性，使得算法很容易收敛到局部最优解。本文分析了这种方法的不足，改进了QGA的信息交流方式，进而提出了一种基于精英组的量子遗传算法 （elite group based quantum genetic algorithm，EQGA）。最后，本文将 EQGA 用于无线多媒体传感器网络 （wireless multimedia sensor network，WMSN）的覆盖优化问题，通过对比实验验证了EQGA的性能。

2 量子遗传算法

QGA是在GA基础上发展起来的一种随机搜索算法。为了进行区别，本文将传统的QGA算法称为标准量子遗传算 法 （standard quantum genetic algorithm，SQGA）。在SQGA中，染色体的编码和演化操作需要借助于量子计算的相关工具，下面分别进行介绍。

2.1 量子比特编码

SQGA算法使用量子比特来表示一个基因位。量子比特的表示如式（1）所示，其中，α、β∈C，且满足|α|2+|β|2=1：

|α|2、|β|2分别表示|0>、|1>状态出现的概率。可以看出，与经典的二进制比特不同，量子比特并不是一个确定的|0>态或|1>态，而是这两种状态的概率叠加。

染色体的编码如式（2）所示，其中，m是染色体含有的基因数，k是每个基因所含有的量子比特数，αxy、βxy的意义与前面相同：

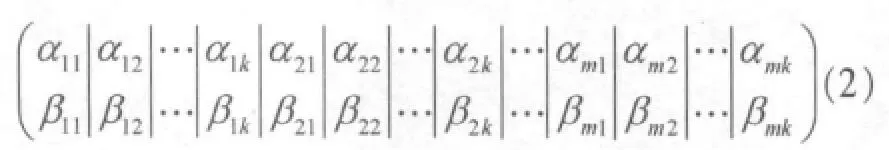
2.2 演化操作

在SQGA中，染色体主要有量子变异和量子旋转两种进化操作。量子变异操作的过程如式（3）所示，量子旋转操作的过程如式（4）所示：

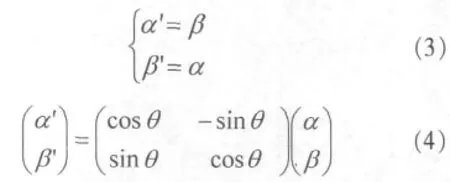
其中，(α,β)、(α′,β′)分别为调整前与调整后的量子比特。式（4）中的θ是量子旋转的角度。

2.3 算法流程

SQGA的流程如下：

（1）设置 SQGA算法的参数，如迭代次数、变异概率等；

（2）初始化种群；

（3）对所有染色体进行评估测量，并记录最优个体作为群体演化的指导；

（4）根据当前的最优染色体，对所有染色体进行量子旋转操作；（5）根据变异概率对所有染色体进行量子变异操作；（6）如果算法终止条件满足，则程序运行结束，否则返回步骤（3）。

2.4 量子遗传算法的不足

SQGA算法的收敛速度大大快于GA算法。其原因除了量子计算的并行性之外，还有一个就是染色体更新时演化目标的选择机制。在SQGA中，每次只选择一个最优染色体来指导群体的进化。每条染色体进化时都以它作为演化目标进行旋转操作，这固然增加了最优染色体在群体中的影响力，促进了优秀信息的传播，并在客观上加速了算法的收敛，但另一方面，所有染色体都向同一个体演化，那些带有合理信息的其他染色体很可能由于暂时的适应度不高而被淘汰，于是算法很容易收敛到局部最优解。SQGA的信息传播结构如图1所示。

图1 SQGA的信息传播结构

3 基于精英组的量子遗传算法

3.1 设计思想

从前面的分析可以知道，每次进化只使用一个染色体来指导整个种群是不合适的，这会导致其他染色体所带有的合理信息不能在种群中保留，从而破坏了染色体的多样性。本文对此进行了改进，提出了EQGA算法。EQGA使用多个染色体来指导群体的进化，这样既可以保证染色体的多样性，算法也不容易收敛到局部解。EQGA的信息传播结构如图2所示。

图2 EQGA的信息传播结构

3.2 染色体精英组

在EQGA算法中，将这些最优的染色体称为染色体精英组。下面介绍精英染色体的产生、维护以及如何对种群的进化发挥影响。

（1）精英组的产生

精英染色体也是由适应度函数评判产生。对染色体进行评估、测量之后，选择适应度最高的t个染色体加入精英组即可。

这里最主要的问题是t值的确定。如果t值过大，不仅计算产生精英组的开销较大，算法的收敛速度也会变慢，反之，如果t值过小，算法又将收敛到局部最优解。通过分析与实验后认为，t值的大小与求解问题相关。如果解空间的局部最优点很多，且幅度变化较大，那么算法陷入局部最优的可能性较大，需要适当增大t的值；如果解空间的变化较为平缓，且局部最优点不多，那么t的值可以相对减小。

（2）精英组的维护

由于种群中的染色体在每次迭代中都会发生更新，因此精英组中的成员也应该同步进行更新，以反映种群的进化。EQGA算法的精英组中一直保留了t条染色体。每次评估完染色体之后，EQGA首先选出t条染色体，然后与精英组中的t条染色体比较，从中选择最优的t条予以保留。

（3）精英组对种群进化的指导

EQGA的染色体更新也主要借助于量子旋转操作实现。与SQGA不同的是，EQGA在选择演化目标时并不使用固定的一条染色体，而是从精英组中随机选择一条。这样就保证了染色体的多样性。

3.3 EQGA算法的流程

EQGA算法的流程如下。

（1）设置EQGA算法的参数，如迭代次数、变异概率、精英染色体数目t等。

（2）初始化种群。

（3）对所有染色体进行评估测量，并更新精英组中的t条染色体。

（4）对每个染色体进行量子旋转更新操作。每次更新时，随机从精英组的t条染色体中选取一条作为演化目标。

（5）根据变异概率对所有染色体进行量子变异操作。

（6）如果算法满足终止条件，则程序运行结束，否则返回步骤（3）。

可以看出，EQGA算法只是在更新精英组时计算量有所加大，但算法的复杂度并没有增加。

4 EQGA算法在WMSN覆盖优化中的应用

4.1 EQGA算法的应用

为了验证EQGA算法的性能，本文将其应用于无线多媒体传感器网络中的覆盖优化问题。

WMSN是一种具有广泛用途的网络，它可以部署在多种场合，对各种环境信息进行采集和监控。WMSN主要由多媒体节点组成，每个节点都有一定的监控范围。通常这个范围可以用一个扇形表示，如图3所示。其中，O表示传感器节点，扇形半径R称为监控距离，扇形角α称为监控视角，扇形对角线称为监控方向。一般情况下，网络部署后节点位置不可再发生变化，但节点的监控方向可以通过旋转摄像头来进行调整。

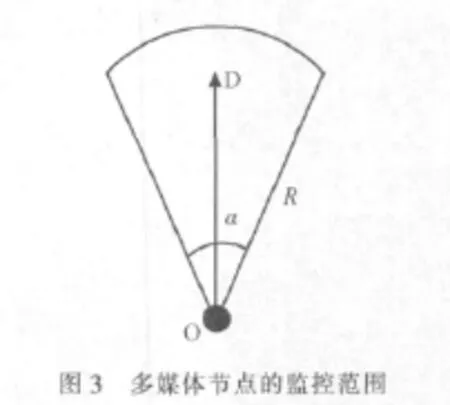
由于部署的不合理和节点电量耗尽等原因，网络中会出现大量的监控重叠与监控盲区。前者浪费了节点的监控能力，后者降低了网络的监控质量，这两种情况都应当避免。为此，需要对网络进行覆盖优化处理，以扩大网络的监控范围。

在不增加节点的情况下，覆盖优化的主要手段就是通过调整各节点的监控方向来实现，其原理如图4所示。

使用EQGA算法来求解各节点的最佳监控方向。

编码时，每个基因就代表一个节点的监控方向。因此，染色体一共由n个基因组成，其中，n是网络中的节点数。

在设计适应度函数时，结合具体问题，使用网络覆盖率来评价染色体的性能。由于重叠区域的形状为非规则图形，因此直接计算覆盖率很困难。所以进行了近似处理，在监控区域中以等距离的方式抽取离散点，如图5所示。

设一共取了psum个点，其中被扇形覆盖了pcoverd个，则网络的覆盖率为：

式（5）为染色体的适应度评估函数。

4.2 仿真测试

在MATLAB环境下进行了仿真测试。首先随机生成了多组WMSN测试场景用例。在这些测试用例中，场景大小300×300 m2固定不变，节点的感知半径为40 m，视角大小为 π/6，节点数量分别为 30、60、90、120、150、180和 210个。对于每个测试用例，分别使用GA、SQGA和EQGA进行监控方向的最优解计算，并记录平均值和最优值。3种算法的相关设置如表1所示。

表1 算法参数

图6是节点数为150个时，3种算法求出的最优解比较，从图中可以看出，EQGA算法的效果最好。

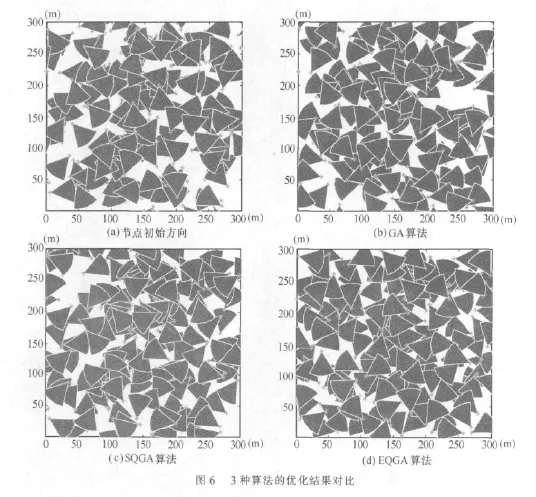
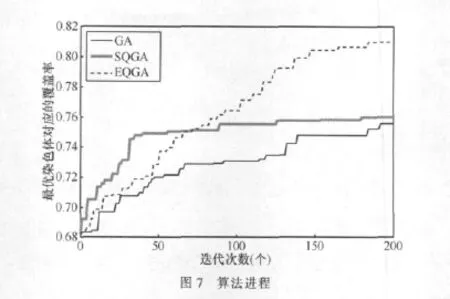
图6中各算法最优解的进化过程如图7所示。GA算法求出的解与SQGA接近，但算法收敛速度较慢。SQGA算法在开始阶段的进化速度很快，但是40次迭代之后进化速度明显降低，说明此时SQGA算法停滞于局部最优解，无法再找到更好的结果。EQGA算法的进化速度优于GA，且程序运行至150次迭代时最优解仍在更新，因此它找到的解最好。这主要是因为它使用了多个最优染色体来指导群体的进化，算法不容易早熟。

3种算法更全面的比较如图8和图9所示。图8是3种算法每个场景的平均结果演示，图9是3种算法每个场景的最优结果演示。通过比较可以发现，EQGA算法求出的解比GA算法和SQGA算法都要好。

5 结束语

标准量子遗传算法使用一个染色体来指导种群的进化，算法的收敛速度较快，但极易陷入局部最优解，本文针对这个缺陷进行了研究，提出了改进的量子遗传算法EQGA。EQGA使用一组染色体来指导种群的进化，能够很好地保持种群的多样性，因而求出的解更优。对于WMSN覆盖优化问题的测试表明，EQGA算法达到了设计的目标。

1 Barolli A,Takizawa M,Xhafa F,et al.Application of genetic algorithms for QoS routing in mobile ad-hoc networks:a survey.In:Proceedings of International Conference on Broadband,Wireless Computing Communication and Applications,Fukuoka,Japan,2010

2 Knysh D S,Kureichik V M.Parallel genetic algorithms:a survey and problem state of the art.International Journal of Computer and Systems Sciences,2010,49(4):579～589

3 Li,Nan,Luo Yi.An improved co-evolution genetic algorithm for combinatorial optimization problems.Lecture Notes in Computer Science,2011,6 728(1):506～513

4 郭鹏,程文明,张则强.求解具有恶化工件单机调度问题的改进遗传算法.西南交通大学学报,2011,46(3):506～511

5 Han K H.Genetic quantum algorithm and its application to combinatorial optimization problem.In:IEEE Proceedings of the 2000 Congress on Evolutionary Computation, LA Jolla,California,USA,2000

6 Xiao J,Yan Y P,Zhang J,et al.A quantum-inspired genetic algorithm for k-means clustering.Expert Systems with Applications,2010,37(7):4 966～4 973

7 Gu J W,Gu M Z,Cao C W,et al.A novel competitive co-evolutionary quantum genetic algorithm for stochastic job shop scheduling problem.Computers&Operations Research,2010,37(5):927～937