基于机器视觉的平面夹角测量方法*

雷经发 王德麾 袁中凡†

(1.四川大学制造科学与工程学院，四川成都610065;2.安徽建筑工业学院机械与电气工程学院，安徽合肥230061)

在机械制造、土木工程、飞行器姿态控制、机械手抓握等诸多领域，两平面间的夹角是一个重要的物理量.目前，测量角度的方法主要有机械测量方法，电磁测角方法，光学测角方法和光电测角方法等［1］.机械测角方法主要为接触式测量，但其测量速度较慢;电磁测角方法是利用电磁感应的原理来测量角度，虽然在测量精度、速度上较机械测量法有较大改进，但仍不能应用于非接触式测量;光学测角方法虽具有较高的精度，但对硬件要求较高，且只限于一维角度测量;光电测角方法是把传统光学方法与光电接收器件相结合，具有精度高、体积小、可维护性好等优点，但其量程一般较小，故应用受到一定的限制［2-3］.

随着计算机和CCD相机性能的提高，机器视觉开始成为一种重要的测量方法，由于具有非接触测量、仅需使用一台或多台数字式相机、可进行实时测量等特点，被迅速地应用于几何量测量、空间运动分析等领域中.文中即提出了一种仅使用一台数字式相机，进行空间两平面夹角的测量方法.

在机器视觉测量中，首先需要进行相机定标，即确定相机的内部参数K、旋转矩阵R和平移向量T［4］.虽目前有多种相机定标方法［5］，但文中借助待测平面上的2个圆标记，仅需相机内部参数K，在空间任意位置进行1次拍照，即可测得两平面法线间的夹角，其补角即为两平面间夹角，简化了平面夹角的测量.

1 平面夹角测量原理及算法

设圆C位于平面π上，圆心为O，经参数为K、R、T的相机成像后，获得如图1所示的图像.圆C和其圆心的像分别为C'、O'.由射影几何及成像方程可知，圆的像是一条二次曲线［6］，用u、v表示图像坐标系中点的坐标，单位为像素;设 A、B、C、D、E为常数，则C'在图像坐标系下的方程可表示为

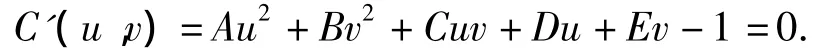
或

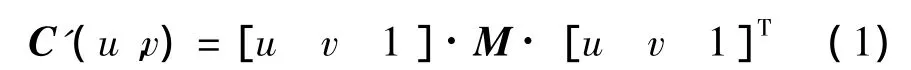
式中:M为二次曲线C'的二次型矩阵.

图1为二次曲线与平面消隐线.图1中直线l'∞是平面π 上无穷远直线l∞的像，称为消隐线.由射影几何知，每个平面上有且仅有一条消隐线，其上的点都是此平面上各方向上的灭点，且同方向的直线具有相同的灭点［7-8］.设(us，vs)为 l'∞上的任意一点，l为一变量，a∞、b∞、c∞为常数，则 l'∞图像坐标系下的方程为:

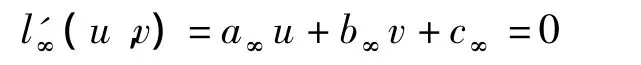
或

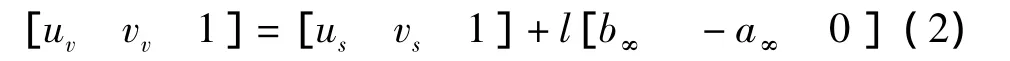
式中:uv、vv为平面上的任意灭点.

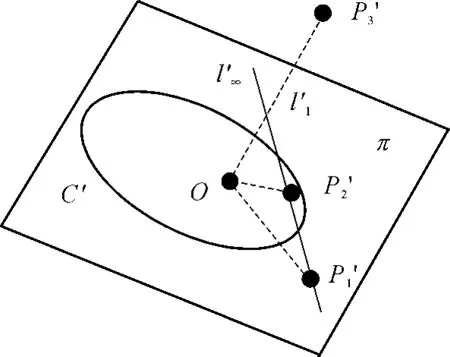
图1 二次曲线与平面消隐线Fig.1 Conic and vanishing line of a plane

如设O'点的坐标为(uo，vo)，由射影几何可知，式(2)中系数 a∞、b∞、c∞满足以下关系［9］:

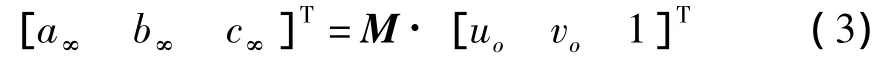
即由平面上一个圆及其圆心的图像，可确定此平面上的消隐线方程.

由文献［9］提出的计算机视觉的平面角度测量方法可知［10］，如已知相机内部参数矩阵 K和［vx1vy1vz1］、［vx2vy2vz2］方向上的灭点坐标(u1，v1)、(u2，v2)，则其夹角 θ满足以下关系:

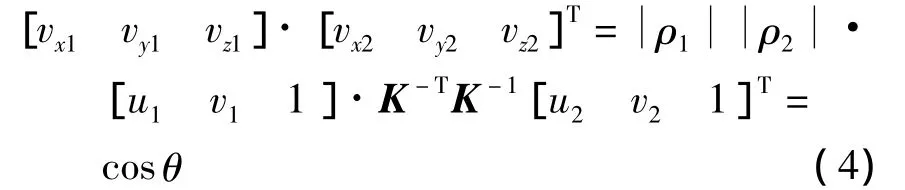
其中 ρ1、ρ2满足以下关系:

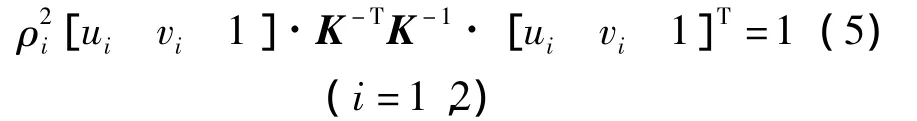
因平面上灭点都位于直线l'∞上［11-12］，则平面上任意灭点(uv，vv)都满足式(2)所示的消隐线方程.如考虑一条垂直于平面π的直线l1，如图1所示.其像为l'1，此方向上的灭点为P'3(u3，v3).可知l1必垂直于平面π上的所有直线，且(u3，v3)和平面π上所有灭点坐标(uv，vv)也必满足式(4)，即有:

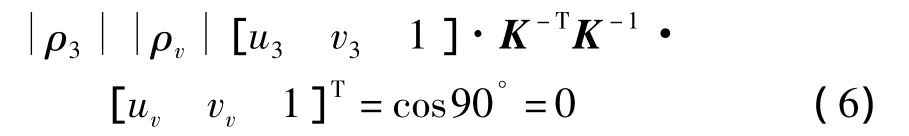
式中:ρ3、ρv分别为与(u3，v3)、(uv，vv)对应的一个常数，可由式(5)确定.将式(2)代入式(6)可得:

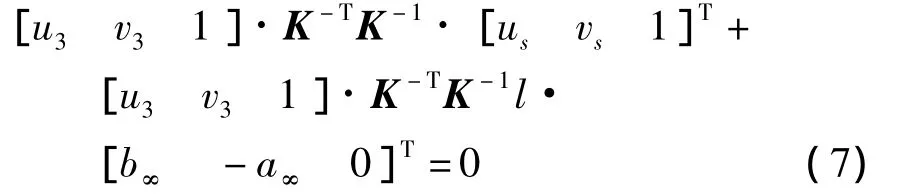
因式(7)对任意l都满足，则必有:

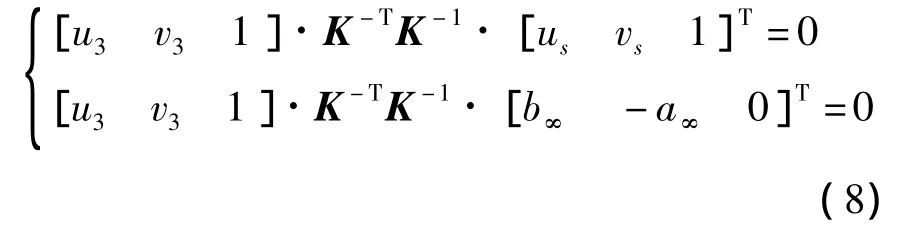
即在已知平面消隐线方程的情况下，由式(8)即可确定此平面法线方向上的灭点坐标.

由以上分析可知，在已知两平面法线方向上灭点坐标 P'3(u3，v3)、P'4(u4，v4)的情况下，先由式(5)计算出ρ3、ρ4，再利用式(4)即可得到两法线间夹角θ的余弦值，通过反三角函数可解得θ，其补角即为平面间夹角.需要说明的是，因式(5)无法确定ρ符号，使得解出的θ可能与其真实值互为补角.通过适当选取拍照角度可解决此问题，避免在被测对象正前或正后位置进行拍照.而在多数角度测量中，待测角度范围恒为锐角或钝角，仅需对θ值进行简单判断、取补即可.

2 测量算法实现

根据以上分析，可得本方法的测量步骤如下.

(1)在两待测平面π1、π2上分别标识出圆C1、C2及其圆心 O1、O2.

(2)用已知内部参数矩阵为K的相机，在空间任意位置进行1次拍照.

(3)拟合圆 C1、C2图像 C'1、C'2的方程;确定圆心O1、O2图像 O'1、O'2的图像坐标.

(4)根据 C'1、C'2的方程和 O'1、O'2的图像坐标，按式(3)计算所在平面上的消隐线方程.

(5)根据式(8)，由消隐线方程计算出各平面法线方向上的灭点坐标;再由式(4)、(5)即可计算出两平面法线间的夹角θ，而两平面间的夹角α即为:α=180-θ.

3 实验

首先用Matlab进行仿真实验以验证测量原理;再借助Mahr PMC 650型三坐标机进行实际的角度测量以验证算法的测量精度和稳定性.仿真实验中，相机内部参数K等于实测出的Canon IXUS500型相机参数值K1;实际实验中，采用SONY DSC-W50型数码相机，其内部参数K=K2.K1、K2具体值如下所示:

3.1 仿真实验

首先由计算机随机生成相机的旋转参数矩阵R、平移向量T;再根据相机成像方程，生成空间两个圆及其圆心的图像，两圆所在平面间的夹角θ为已知，作为理论值使用.处理数据时，仅把生成的图像和相机内部参数矩阵K作为已知数据，用本算法计算出两平面间的夹角并与理论值进行比较.

仿真实验用角 -轴法生成旋转矩阵 R［13］.［vxvyvz］为单位轴向量，η为转角，则旋转矩阵为

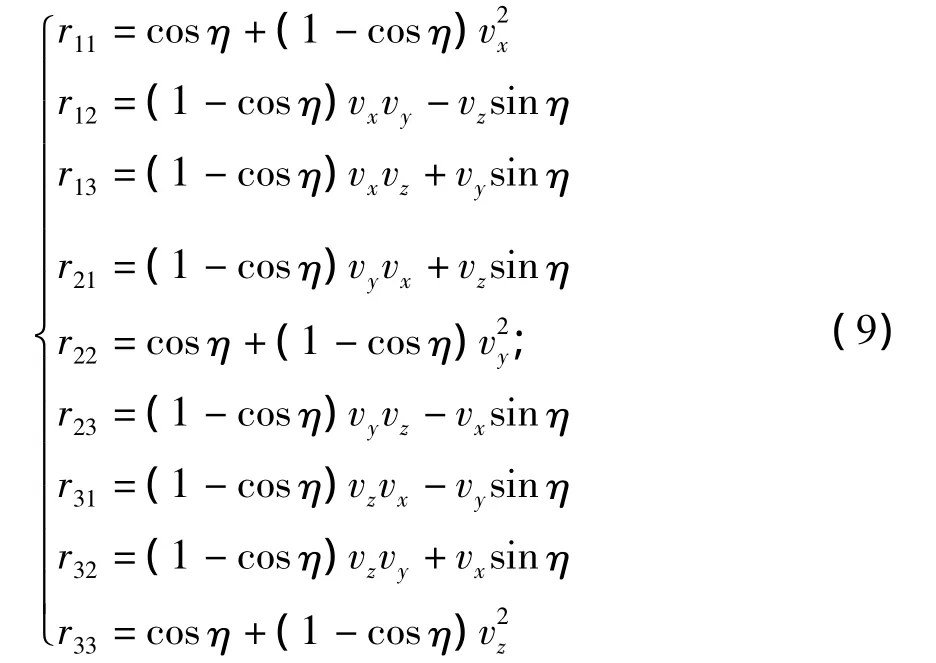
式中:rij为旋转矩阵R中第i行，第j列的元素.

设定夹角为钝角进行第1次实验.图2(a)、(b)分别是实验1的仿真场景图和相机获得的图像数据.图 2(b)中 p1、p2点为圆心图像;C'1、C'2是平面上标识圆图像.通过图像处理算法，可获得C'1、C'2上各点和p1、p2的图像坐标值.如C'1上各点坐标为(uci，vci)，i≥5，则由式(1)可得方程:

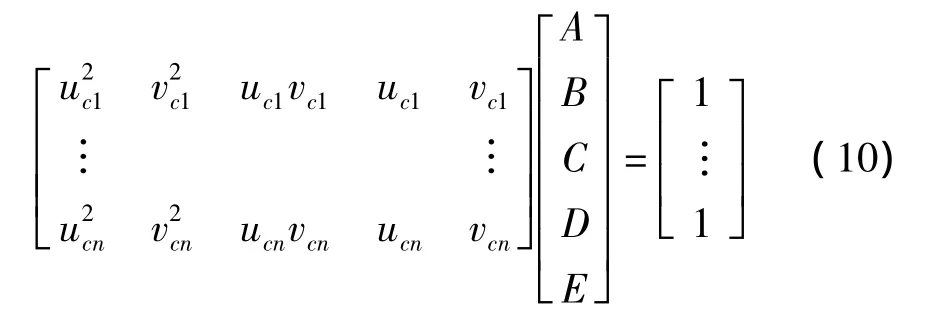
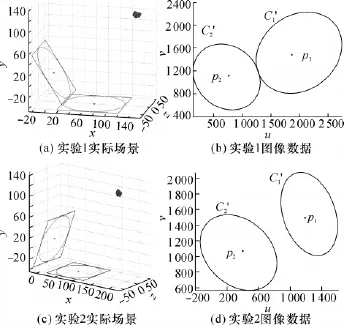
图2 仿真实验相关数据Fig.2 Images of simulations

由线性代数中的广义逆矩阵理论［14］，可解出参数［A，B，C，D，E］的最小二乘解，即得到椭圆 C'1的拟合方程，同理解出C'2的方程;然后把得到的数据代入式(3)、(4)、(5)、(8)中即可.用［A，B，C，D，E，-1］表示 C'1、C'2方程参数;［u，v］表示圆心 p1、p2坐标;［a∞，b∞，c∞］表示消隐线 l'∞方程参数，则具体实验数据如表1所示.

改变相机外部参数，令夹角为锐角进行第2次实验，如图2(c)、(d)所示.结果见表2.

表1 仿真实验1数据处理结果Table 1 Data of simulation one

表2 仿真实验2数据处理结果Table 2 Data of simulation two

3.2 利用三坐标机的角度测量实验

为进一步验证本算法，借助Mahr PMC 650型三坐标机进行实验.平板π1、π2上分别贴有如图3所示的圆形标识.标识上直线l1、l2是圆的两条直径，用以精确确定圆心图像坐标.世界坐标系设定为三坐标机的坐标系.平板π1平置于测量台上，即处于世界坐标系的x-y平面;平板π2立于平台上，如图4所示;然后用SONY DSC-W50型相机，在空间任意位置处对两平板进行1次拍照，获得图像的宽度×高度为2816像素×1872像素，相机内部参数矩阵已知;通过对所获图像进行二值化、目标提取、椭圆和直线拟合等处理，并由式(3)、(4)、(5)、(8)即可得到平板π1、π2间的夹角值 α.

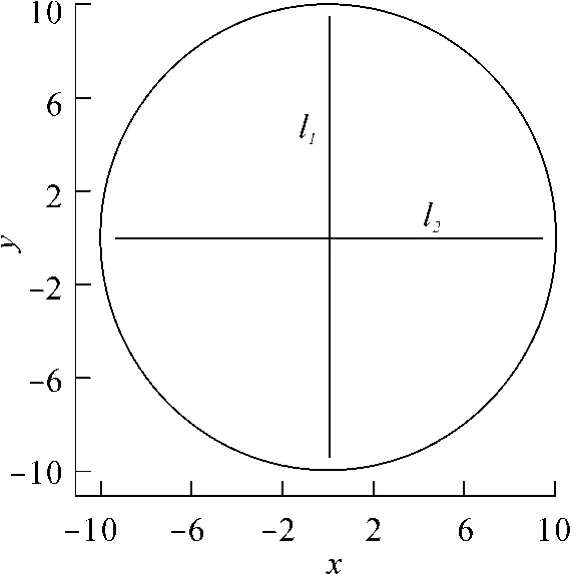
图3 实验用圆标识图Fig.3 Marking graph used in experiments

图4 实验原理图Fig.4 Diagram of experimental principle

为评估本方法的精度，用三坐标机测量平面π2上至少3个点(非共线)的坐标以拟合其平面方程，进而得其与平板π1间的夹角θ.鉴于三坐标机具有极高的测量精度，故把θ值作为理论值，而把文中方法得到的夹角值α作为测量值.按照以上实验步骤，进行3组实验，如图5所示.

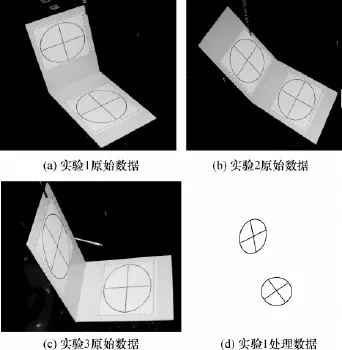
图5 实验相关数据(局部)Fig.5 Data of experiments(partial picture)

以实验1为例简述数据处理过程.首先采用阈值法二值化图像［15］，利用Matlab中的bwselect()函数进行目标提取［16］，得到两标识圆及4条直径上所有点的图像坐标，如图5(d)所示;利用式(10)拟合出两标识圆图像的方程;利用直线最小二乘法拟合出4条直径图像的直线方程;联立同圆上两直径图像方程，即解出圆心图像的坐标;把圆标识图像方程、圆心图像坐标代入式(3)中，得到此平面上消隐线方程参数;把消隐线方程参数、相机内部参数代入式(8)中，得到平面法线方向上的灭点坐标;最后把两平面法线方向上的灭点坐标、相机内部参数代入式(5)、(4)中，即可得到2平面法线间的夹角，进而得到平面间的夹角值.

本实验中通过拟合平板π2上6个非共线点得到理论夹角值θ.以实验1为例，三坐标机测得的6个点坐标数以(x，y，z)形式表示，单位为 mm.点坐标为(-171.630，-303.462，6.089)，(-142.669，-304.285，9.063)，(-166.039，-303.116，9.048)，(-161.050，-301.812，15.947)，(-129.166，-305.573，5.807)，(-129.091， -303.963，13.496).拟合出的π2平面方程为

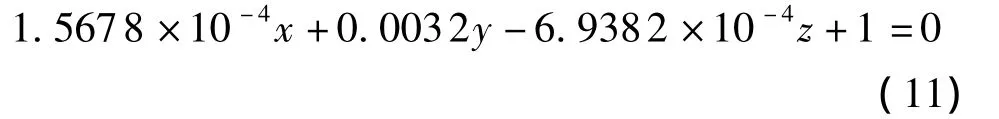
式(11)所示的平面法向量为［1.5678×10-4，0.0032，-6.9382×10-4］，因已确定平面夹角为钝角，则得其与x-y平面夹角为102.2465°，此值即为理论值.具体实验数据如表3所示.

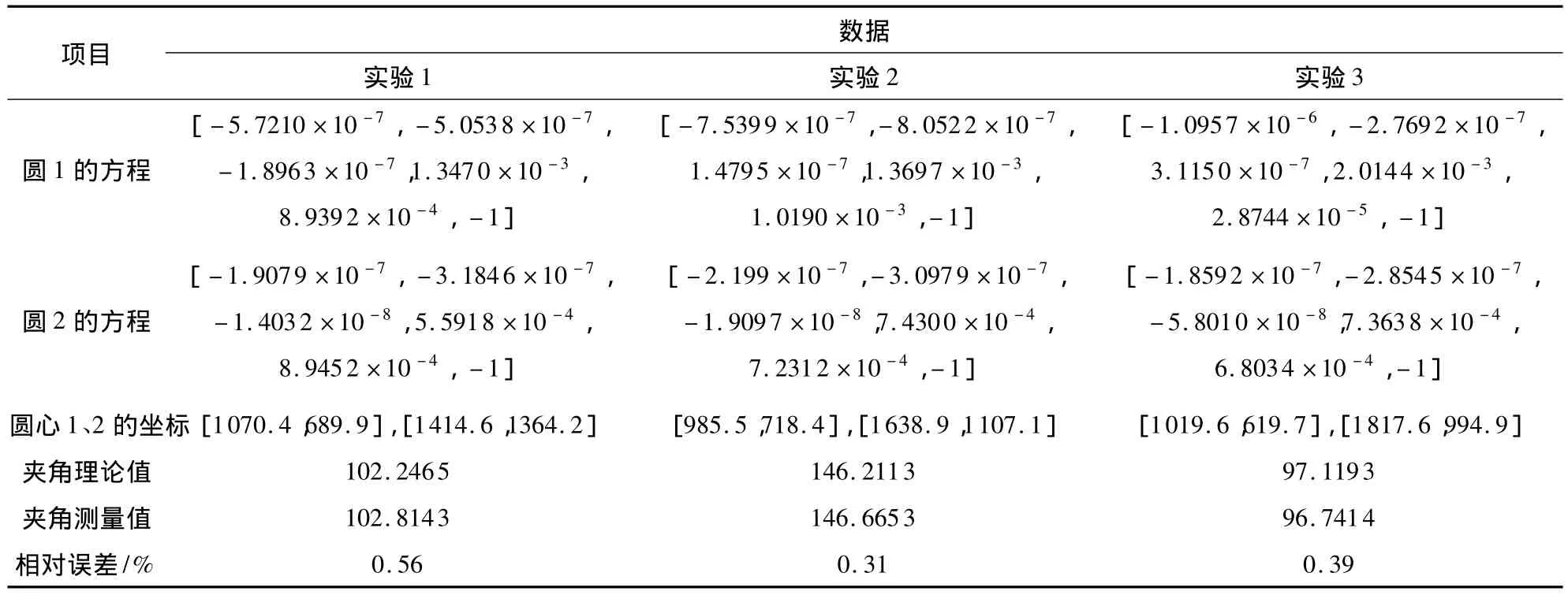
表3 实验结果Table 3 Experimental results

由表3中的数据可以看出，文中方法具有较高的测量精度，相对测量误差小于1%.

4 结论

文中提出的基于机器视觉的平面夹角测量方法无需已知相机的旋转矩阵和平移向量参数，故无需对相机进行复杂的全参数定标，具有使用简单、快捷的特点;进行测量时仅需对待测平面进行1次拍照，获得2平面上部分标记圆图像和其圆心图像即可，因此可以根据实际的测量环境，在较大范围内自由地设置相机位置，使得此方法具有较高的灵活性;在数据处理过程中，二次曲线、直线方程都由最小二乘法拟合得到，保证了标识圆图像方程、直径图像方程的精度，进而有效地提高了消隐线方程的计算精度和最终的测量精度.

由实验结果可知，文中方法具有较好的测量精度，相对误差在1%以内.通过理论分析及实验可知，标记圆图像的方程拟合误差、圆心图像坐标求解误差是影响测量精度的最主要因素，通过保证采集图像的清晰度、选用高分辨率相机可以解决这一问题，能够满足机械、地质、控制、人机工程等领域内的非接触平面夹角测量要求.

［1］Yu L F，Pedrini G，Osten W.Three-dimensional angle measurement based on propagation vector analysis of digital holography［J］.Appl Opt，2007，46(6):3539-3545.

［2］Shang H M，Toh S L，Fu Y，et al.Measurement of angle of rotation using circular optical grating［C］∥Proceedings of SPIE Second International Conference on Experimental Mechanics.San Diego:SPIE Press，2001:72-78.

［3］吕日好，赵长寿，杨中文.空问目标姿态角测量计算方法研究［J］.仪器仪表学报，2006，27(6):1211-1212.Lu Ri-hao，Zhao Chang-shou，Yang Zhong-wen.Research on computational method for extended target posture angle［J］.Chinese Journal of Scientific Instrument，2006，27(6):1211-1212.

［4］Faugeras O.Three-dimensional computer vision:a geometric view point［M］.Cambridge:The MIT Press，1993:30-52.

［5］刘苏宜，王国荣，石永华.激光视觉机器人焊接中摄像机和手眼的同时标定［J］.华南理工大学学报:自然科学版，2008，36(2):74-77，82.Liu Su-yi，Wang Guo-rong，Shi Yong-hua.Simultaneous calibration of camera and hand-ege in robot welding with laser vision ［J］.Journal of South China University of Technology:Natural Science Edition，2008，36(2):74-77，82.

［6］Hartley Richard，Zisserman Andrew.Multiple view geometry in computer vision［M］.Cambridge:Cambridge University Press，2000.

［7］方德植，陈奕培.射影几何［M］.北京:高等教育出版社，1983.

［8］Wu Yi-hong，Hu Zhan-yi，Wu Fu-chao.Camera calibration from the quasi-affine invariance of two parallel circles［C］∥Proceedings of European Conference on Computer Vision.Prague:ECCV Press，2004:190-202.

［9］苏步青.高等几何学五讲［M］.上海:上海教育出版社，1991:15-32.

［10］王德麾，袁中凡，樊庆文.利用计算机视觉的平面角度测量方法［J］.西南交通大学学报，2010，45(5):775-779.Wang De-hui，Yuan Zhong-fan，Fan Qing-wen.Planar angle measurement based on computer vision［J］.Journal of Southwest Jiaotong University，2010，45(5):775-779.

［11］马颂德，张正友.计算机视觉-计算理论与算法基础［M］.北京:科学出版社，1998.

［12］Tsai R Y.An efficient and accurate camera calibration technique for 3D machine vision［C］∥Proceedings of IEEE Conference of Computer Vision and Pattern Recognition.Florida:IEEE Press，1986:364-374.

［13］Hartley R.Self-calibration of stationary cameras［J］.Computer Vision，1996，22(1):5-23.

［14］程云鹏.矩阵论［M］.西安:西北工业大学出版社，2005.

［15］张文耀.光电图像处理［M］.北京:电子工业出版社，2002.

［16］樊庆文.基于数字图像的空间大尺寸测距原理和方法研究［D］.成都:四川大学制造科学与工程学院，2008.