自适应模糊PID控制器在开关磁阻电机中的应用
吴 韧,郝润科,崔以田
(上海理工大学光电信息与计算机工程学院,上海200093)
1 引言
开关磁阻电动机传动系统(SRD)是一种新型机电一体化无级调速系统,系统可靠性高,调速范围宽,可以实现高启动转矩和低启动电流,适用于频繁启停和正反转运行的场合。但由于开关磁阻电机(SRM)的双凸极结构及磁路的严重非线性,使得SRD成为一个多变量强耦合、非线性较为严重的系统。运行中呈现的转矩脉动大以及噪声严重影响了SRD的应用[1]。而自适应模糊控制无需被控对象的精确数学模型,适合于非线性、变结构系统。因此引入自适应模糊控制和传统的PID控制结合起来,构建自适应模糊PID控制器应用于SRD系统。该控制器能够通过在线调整比例因子,以适应被控对象特性的变化,达到控制灵活、精度高的效果。
2 SRM 的数学模型[2]
SRM电机的动态特性包括电气部分、机械部分和机电联系部分,可用以下方程来描述。
2.1 电压方程
忽略各相间的相互作用,SR电机第k相的电压平衡方程为:

其中uk、Rk、ψk分别为第k相绕组上的电压、电阻、电流和磁链。由于磁链是关于电流和转子位置的函数,因此上式可写成:

从上式可以得出相电流的表达式如下:
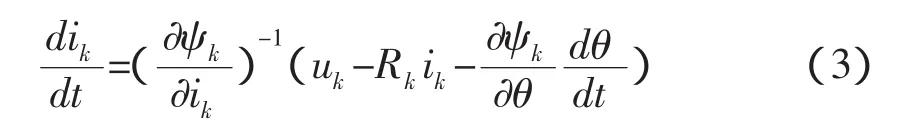
2.2 机械运动方程
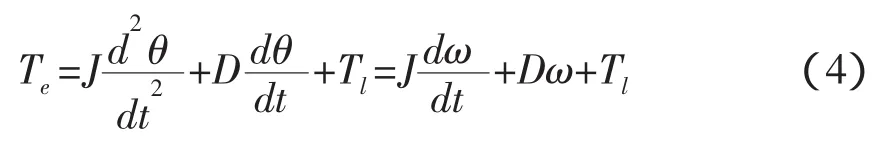
其中:Te为电磁转矩,J为系统的转动惯量,D为摩擦系数,Tl为负载转矩,θ为转子位置角,ω为电机角速度。
由式(4)可得速度表达式为:
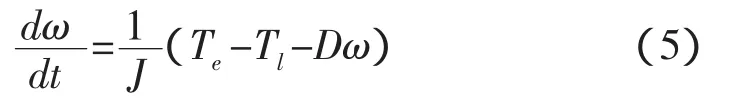
2.3 机电联系方程

其中:Wk(i,θ)、Tk分别为第 k 相的磁场储能和所产生的电磁转矩。一相的模型表达式如图1所示。
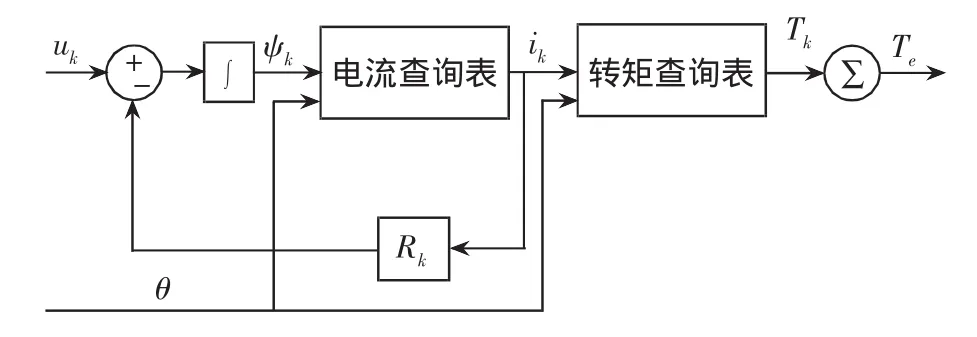
图1 SRM一相数学模型
本文以三相6/4极SR电机为研究对象,三相组合后得到6/4极SR电机的动态模型如图2所示。
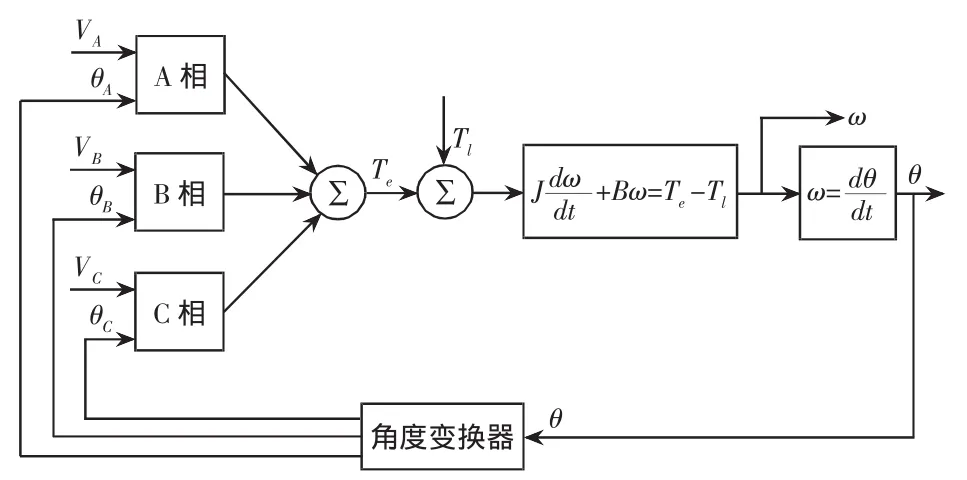
图2 6/4极SRM的动态模型
3 SRM的自适应模糊PID控制
自适应模糊PID控制器是以转速偏差E和转速偏差变化率EC作为输入,根据模糊控制系统的性能在线地整定比例因子、和。使它们保持合适的数值,从而使系统的性能达到令人满意的效果,采用模糊PID控制的开关磁阻电机调速系统框图如图3所示。

图3 模糊自适应PID控制的开关磁阻电机调速系统框图
3.1 模糊控制器
(1)模糊控制器的输入输出变量
自适应模糊PID控制器选取转速偏差E(E=n*-n)和转速偏差变化率 EC=(de/dt)为输入变量,输出变量有3个,即和
(2)输入输出变量的模糊语言描述
考虑到电机转速偏差范围大及高精度的特点,将输入模糊变量偏差量E、偏差量变化率EC对应的模糊语言变量的论域界定在[-3,3],输出模糊变量和的取值范围分别为[-0.1,0.1],[-1,1],[-0.001,0.001],语言值分别取负大、负中、负小、零、正小、正中、正大,即{NB,NM,NS,ZO,PS,PM,PB},其隶属度函数均为正态分布和三角分布相结合。当曲线密度较小时,控制灵敏度较高;密度较大时,模糊控制器的鲁棒性较好,隶属度函数曲线分别为图 4(a)、(b)所示。
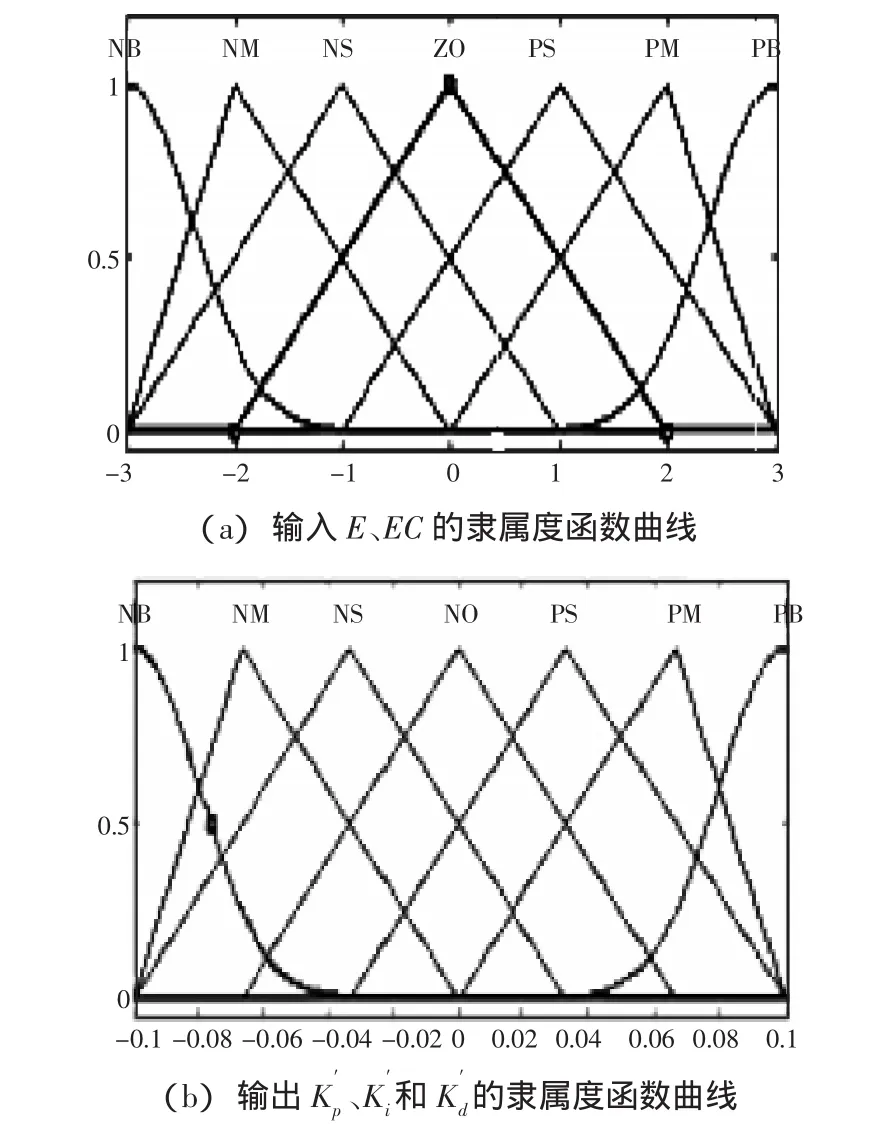
图4 隶属度函数曲线
表1 、和 的模糊控制规则
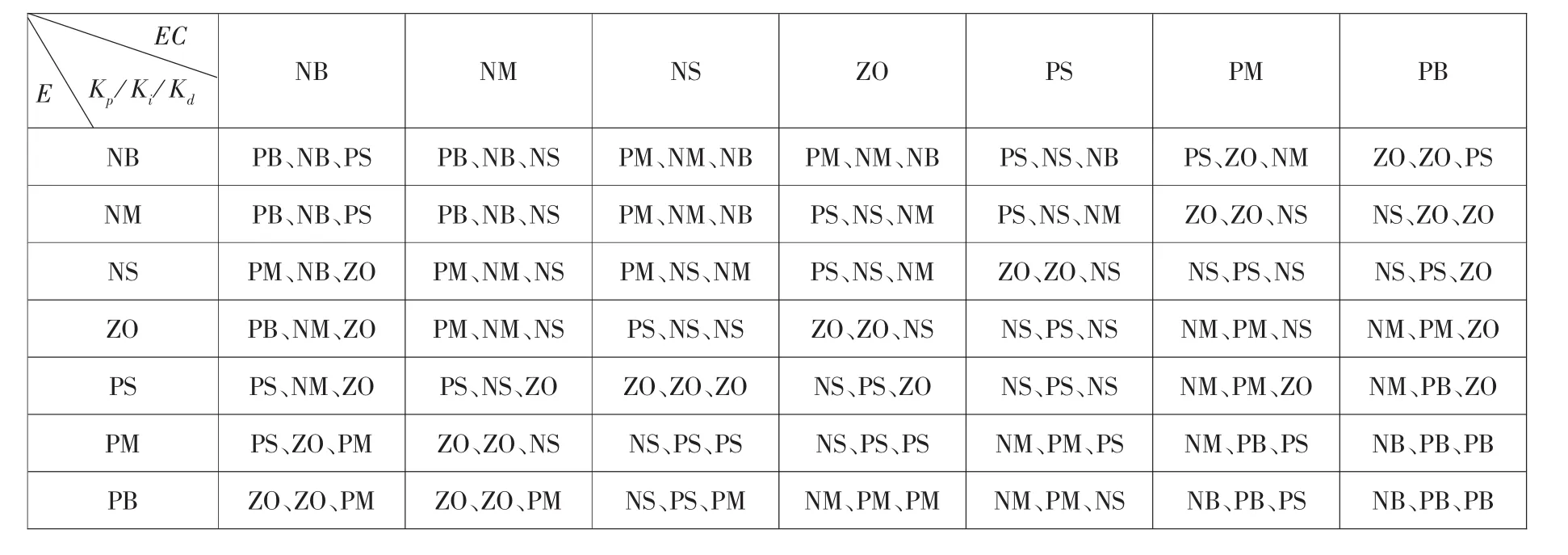
表1 、和 的模糊控制规则
EC E Kp/Ki/Kd NB NM NS ZO PS PM PB NB PB、NB、PS PB、NB、NS PM、NM、NB PM、NM、NB PS、NS、NB PS、ZO、NM ZO、ZO、PS NM PB、NB、PS PB、NB、NS PM、NM、NB PS、NS、NM PS、NS、NM ZO、ZO、NS NS、ZO、ZO NS PM、NB、ZO PM、NM、NS PM、NS、NM PS、NS、NM ZO、ZO、NS NS、PS、NS NS、PS、ZO ZO PB、NM、ZO PM、NM、NS PS、NS、NS ZO、ZO、NS NS、PS、NS NM、PM、NS NM、PM、ZO PS PS、NM、ZO PS、NS、ZO ZO、ZO、ZO NS、PS、ZO NS、PS、NS NM、PM、ZO NM、PB、ZO PM PS、ZO、PM ZO、ZO、NS NS、PS、PS NS、PS、PS NM、PM、PS NM、PB、PS NB、PB、PB PB ZO、ZO、PM ZO、ZO、PM NS、PS、PM NM、PM、PM NM、PM、NS NB、PB、PS NB、PB、PB
(3)模糊控制规则的语言描述[3-4]
根据对SRM调试经验,确定模糊控制规则:当E>0时,即实际转速低于给定转速,要求转速上升;当E<0时,即实际转速高于给定转速,要求转速下降;若 EC<0,则电机加速,当 EC>0,则电机减速,综合考虑E和EC的影响以及系统的稳定性,防止不必要的超调,得到如表1中的49条模糊控制规则。
由于自适应参数的整定通常由专家经验实际操作反复调整,直至自适应模糊控制策略比较完善,根据上述模糊控制规则,得出修正参数的公式如下:
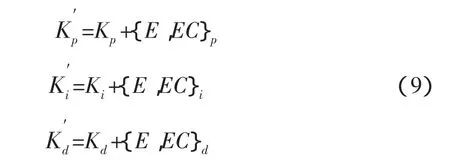
其中:Kp、Ki和Kd为模糊PID控制器3个参数的初始值,本文中 Kp、Ki和 Kd分别取 0.06、0.045 和 0.0005。{E,EC}为偏差E和偏差变化率EC的修正输出。
3.2 PID 控制器

式中:u(n)、e(n)分别为第 n 个采样时刻的控制量和转速差;TI、TD分别为积分、微分时间常数;T为采样周期。
4 仿真实验
Matlab模糊控制工具箱提供的FIS(Fuzzy Inference System)编辑器是一种方便的模糊控制器编辑工具,在Matlab的命令窗口中运行Fuzzy,进入模糊编辑器,选择控制器类型为Mamdani,通过Edit菜单分别输入E、EC和的隶属函数和量化区间,以if…then的形式输入模糊控制规则,模糊决策采用最大最小法,反模糊化采用重心法,这样就建立了一个FIS系统文件,取名为fuzzyadappid,在Simulink里选择Fuzzy logic controller模块,键入名字为a,在Matlab command window里输入a=readfis ('fuzzyadapid'), 完 成 模 糊 工 具 箱 和Simulink的链接。将模糊控制器和PID控制器分别封装后连在一起就构成了复合控制器[5-6]。
5 结果分析
根据以上设计的自适应模糊PID控制器,对参数为三相6/4极的SRM进行仿真分析,SRD仿真参数为:直流电压为240V,定子转子电阻为0.05Ω,转动惯量为 0.05kg·m2,摩擦系数为 0.02N·m·s,给定转速为400rpm。曲线a、b分别为PID控制和模糊自适应PID控制,两种控制方式对比的启动过程仿真波形如图5所示。由图5中可以看出,采用模糊自适应PID控制器比PID控制的系统超调量明显减少,调节时间也缩短很多,在t=0.3s时加负载1N·m后,系统能快速地达到稳定的状态(400rpm)。
模糊自适应PID控制器结合了模糊控制和PID控制的优点,使得SRD系统超调量小,动态性能好,稳态精度高,抗干扰和鲁棒性较强。因此该控制器比较适用非线性、多变量强耦合的开关磁阻电机调速系统。
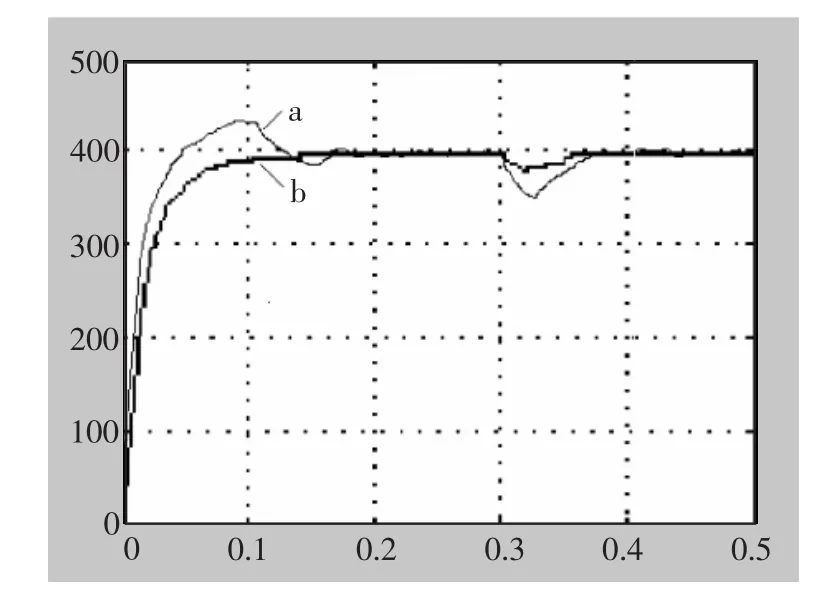
图5 PID控制和模糊自适应PID控制仿真波形
[1]孙建忠,白凤仙.特种电机及其控制[M].北京:中国水利水电出版社,2005.
[2]Ercument karakas,soner vardarbasi.Speed control of SR motor by self-tuning fuzzy PI controller with artificial neural network[J].Sadhan .2007,32(5):587–596.
[3]张国良,邓方林著.模糊控制及其MATLAB应用[M].西安:西安交通大学出版社,2002.
[4]王 辚,张 科.基于MATLAB的自整定模糊PID控制系统[J].探测与控制学报,2008,30(2):73-76.
[5]米芳芳.开关磁阻电机调速控制系统的研究[D].哈尔滨工程大学硕士论文.
[6]刘金琨.先进PID控制及其MATLAB仿真[M].北京:电子工业出版社,2003.

