N,Ga共掺杂对ZnO光学性质的影响
孙正昊,韦 韧,刘玮洁,孙 源,冷 静
(长春工业大学 基础科学学院,吉林 长春 130012)
0 引 言
常温常压下ZnO为六方纤锌矿结构,具有直接带隙,禁带宽度为3.37eV,激子束缚能高达60meV,在电学、光学以及磁学等方面具有巨大的应用潜力,是一种新型的半导体光电材料。近年来,人们对ZnO材料做了大量实验与理论方面的研究工作。自然环境下未掺杂的ZnO具有一些天然缺陷,如氧空位、锌填隙,是一种N型导电材料,如何获得稳定的P型导电材料是当前ZnO半导体材料研究的热点之一,现在理论上倾向于采用N和Ⅲ族元素共掺杂来获得P型导电的ZnO薄膜材料。如陈琨[1]等利用第一性原理计算方法对N,In共掺杂实现P型ZnO进行了研究,张金奎[2]等研究了 N,Al掺杂,赵慧芳[3]等研究了N,Ga掺杂;此外,人们对ZnO光学性质也非常感兴趣,如刘建军[4]研究了Ga原子掺杂对ZnO光学性质的影响。事实上通过对掺杂材料的光学性质进行研究,可以更加深入地了解掺杂对材料电子结构以及能态密度的改变。文献[3]只研究了N,Ga共掺杂对ZnO电学性质的影响,而没有考虑N,Ga共掺杂对ZnO光学性质的影响,文中从第一性原理出发,考虑不同掺杂构型,采用超胞模型计算了N,Ga共掺杂对ZnO材料光学性质的影响,并对其进行了理论分析。
当前,在各种新材料研究中,第一性原理计算方法已经被广泛地采用,从微观角度来研究和预测材料的电学、光学以及磁学等宏观物理性质,是目前对半导体材料电子结构及光学性质计算较为准确的理论方法之一。
1 模型建构与计算方法
1.1 模型建构
理想ZnO晶体属于P63mc空间群,对称性为,晶格常数a=b=0.324 9nm,c=0.520 6nm,α=β=90°,γ=120°,其中c/a为1.602,沿c轴方向的Zn-O键长为0.199 2nm,而其它方向为0.197 3nm,其晶胞由氧原子的六角密堆积和锌原子的六角密堆积反向套构而成。
计算中采用沿ZnO原胞基矢方向扩展两个单位得到的超晶胞,包含32个原子,并考虑了在ZnO基体中4种可能的N,Ga排列构型,如图1所示。

图1 ZnO基体中4种可能的N,Ga排列构型
1.2 计算方法
文中计算由 Materials Studio 5.5软件中的CASTEP软件包完成,CASTEP是一个基于密度泛函理论结合平面波赝势方法的从头算量子力学程序。计算中采用超软势描述离子实与价电子之间相互作用,电子之间交换关联能采用GGAPBE方法,平面波截断能Ecut选取为500eV,自洽收敛精度为5×10-7eV/atom,总能量和电荷密度在对Brillouin区的积分计算使用Monkhorst-Pack方案时选择k网格点为5×5×4,快速傅里叶变换(FFT)网格取48×48×80,每个原子能量收敛精度为5×10-6eV,原子间相互作用力收敛精度设为0.1eV/nm,晶体内应力收敛精度为0.02GPa,原子最大位移收敛精度为5×10-3nm,各原子的价电子组态分别选取为O-2s22p4,Zn-3d104s2,N-2s22p3,Ga-3d104s24p1。
2 计算结果与讨论
2.1 几何结构优化结果
为了研究掺杂对ZnO光学性质的影响,首先对ZnO在未掺杂和4种不同掺杂情况下的几何结构进行优化,计算结果见表1。
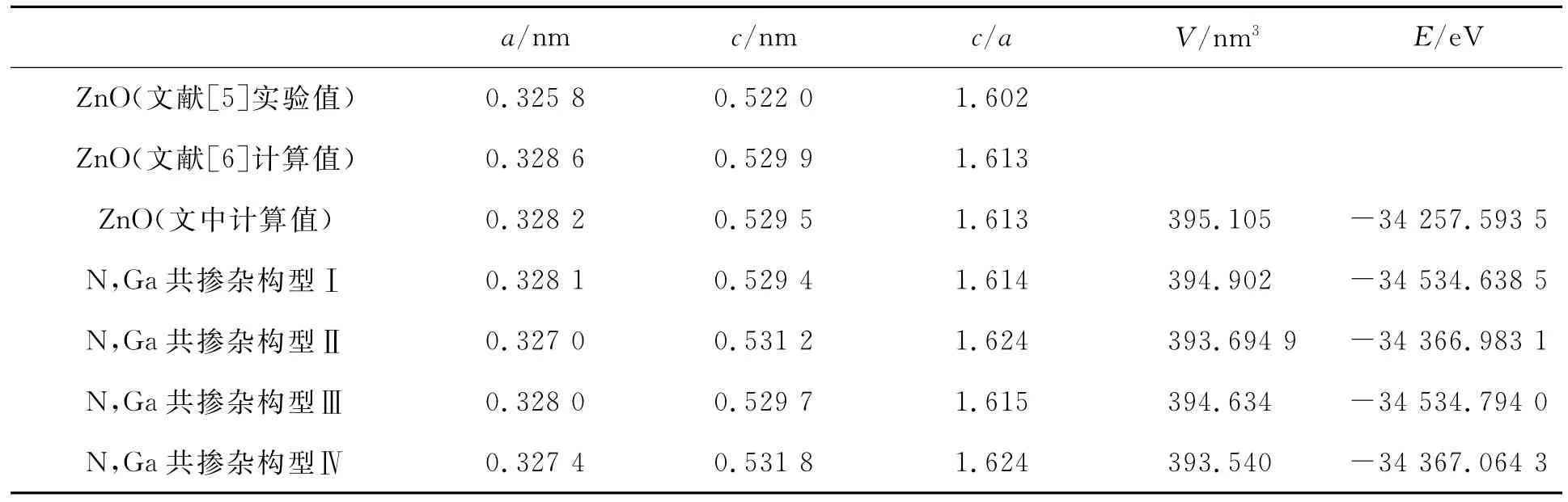
表1 未掺杂ZnO和N,Ga不同构型共掺杂ZnO的几何优化结果与实验值和其它理论计算值比较
从表1可以看出,对于未掺杂ZnO,文中的计算结果与实验值以及其它文献的计算结果符合的很好。对于N,Ga共掺杂ZnO,计算结果表明,不同掺杂构型都导致ZnO晶胞体积缩小,并且掺杂两个N原子比掺杂一个N原子体积缩小的效果更明显,我们分析后认为这是由于掺杂后,Ga-N之间的相互作用较之Zn-O之间的相互作用更强,导致离子键长减小造成的。此外,不同掺杂构型体系总能均低于未掺杂体系,掺杂一个N原子的构型Ⅰ和Ⅲ之间能量近似,掺杂两个N原子的构型Ⅱ和Ⅳ能量近似,而且构型Ⅰ和Ⅲ比Ⅱ和Ⅳ能量更低,原因在于Zn-N键会使体系的能量升高。
2.2 能带结构分析
利用几何优化后的晶体结构,我们计算了未掺杂ZnO以及4种不同掺杂构型的能带结构和态密度,计算结果如图2所示。

图2 未掺杂ZnO以及4种不同掺杂构型的能带结构和态密度
为了清楚地显示出掺杂对能带结构的影响,我们只绘出了-3.0~4.5eV部分的能带图,并以费米能级作为坐标零点。
图2(a)是未掺杂ZnO的能带图,从图中可以看出,未掺杂ZnO是一种直接带隙半导体,导带底和价带顶均位于布里渊区高对称点Г处,带隙值为0.746eV,与文献[6]的理论计算结果(0.74eV)是一致的,小于实验值3.37eV,这是因为第一性原理计算是一个基态理论,在计算中往往过高估计相关能以及基态内聚能,并且低估总交换能,既使采用广义梯度近似,也只是部分改进了原子交换能和相关能的计算结果,依然低估带隙,文中由于过高估计了Zn 3d电子的能量,使得O 2p与Zn 3d之间的相互作用增大,造成价带带宽增大,带隙值偏低,但并不影响对计算结果的理论分析。
从不同掺杂构型的能带结构可以明显看出,掺杂对晶体的完整性产生了破坏,在杂质原子周围由于电失衡形成晶场,在晶场作用下能级发生了劈裂。另外从图中还可以看出,4种掺杂构型的能带依然是直接带隙结构,其中掺杂一个N原子与Ga原子的构型Ⅰ与Ⅲ杂质能级位于费米能级以下,这是由于在ZnO中,Ga原子是施主杂质,N原子是受主杂质,由于掺杂浓度相同,杂质高度补偿作用使得杂质能级完全占据,而掺杂两个N原子的构型Ⅱ和Ⅳ则在禁带中出现了部分填充的受主杂质能级。
2.3 态密度分析
构型Ⅳ的态密度如图3所示。

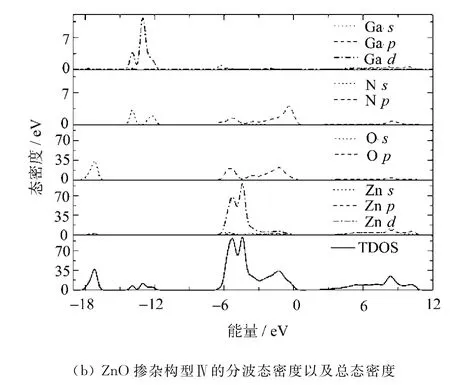
图3 构型Ⅳ的态密度
由于4种掺杂构型的态密度图分布相似,文中只列出构型Ⅳ的态密度图作为说明。
计算结果表明,掺杂后与掺杂前相比,所有构型中O原子的分波态密度2s,2p峰均向低能方向轻微移动,并且分布略微变宽,局域化程度略微减弱,Zn原子的s,p,d分波态密度也出现同样变化,但对总态密度的贡献没变。掺杂后,4种不同掺杂构型的总态密度图中都在-16~-12eV附近出现了新的态密度峰,是由掺杂原子Ga的3d轨道和N的2s轨道强烈杂化形成的。由于Ga原子的3d态与N原子的2p之间较强的吸引势,使得杂质能级发生变化。通过计算发现,构型Ⅰ和Ⅲ之间,构型Ⅱ和Ⅳ之间,在态密度分布数值方面只是略有差别,总的变化趋势是一致的。但掺杂两个N原子的构型Ⅱ和Ⅳ与掺杂一个N原子的构型Ⅰ和Ⅲ相比,由于具有更强的受主-受主排斥作用,N的2p态局域化特征更加明显,并向高能方向移动,形成更深的受主能级。
2.4 光学性质
为了准确分析掺杂给ZnO带来的光学性质的改变,我们采用剪刀算符来处理实验值与计算值之间的差值,这种方法在其它工作中也广泛采用[7]。
2.4.1 吸收光谱
吸收光谱如图4所示。
计算结果表明,未掺杂的ZnO在3eV附近有一吸收边,对应电子从价带向导带的跃迁吸收,两个主要的吸收峰分别位于9.83eV和14.32eV处,峰值分别为1.2×105cm-1和3.4×105cm-1,来自Zn 3d 到 O 2p 以及 O 2s到Zn 3d的轨道间跃迁。

图4 吸收光谱
从图4(b)可以看出,掺杂后构型Ⅰ,Ⅱ,Ⅳ在可见光到近紫外区(1.6~4.0eV)出现新的吸收峰。经过分析,我们认为这是电子由受主杂质能级N 2p向导带跃迁产生的。由于N掺杂在带隙中产生受主杂质能级,电子从价带跃迁到受主杂质能级以及从受主杂质能级跃迁到导带所需的能量与未掺杂时相比变小,相应地吸收光子的能量也减小,因此产生对可见光以及近紫外光的吸收。从图中可以看出,不同掺杂构型产生的峰值不同,构型Ⅳ产生的峰值最大,为0.7×105cm-1;构型Ⅱ的峰值次之,为0.6×105cm-1;构型Ⅰ的峰值为0.4×105cm-1;构型Ⅲ产生的吸收峰虽不明显,但对可见光及近紫外光的吸收依然比未掺杂ZnO的大。吸收峰值的大小不同,与杂质能级的态密度有关,态密度大的容纳电子数量多,光吸收强度大。从态密度计算结果来看,在文中的4种掺杂构型中,在费米能级附近的N 2p态密度是构型Ⅳ峰值最大,并且构型Ⅳ>Ⅱ>Ⅰ>Ⅲ,符合上述分析。
在高能区,构型Ⅰ和Ⅱ的吸收谱线与未掺杂ZnO谱线近似,但构型Ⅲ和Ⅳ的吸收谱线与未掺杂ZnO谱线相比,主吸收峰向低能方向移动2eV左右,并且吸收系数峰值下降为2.8×105cm-1,吸收区域变窄。
2.4.2 介电函数
随光子能量变化曲线如图5所示。
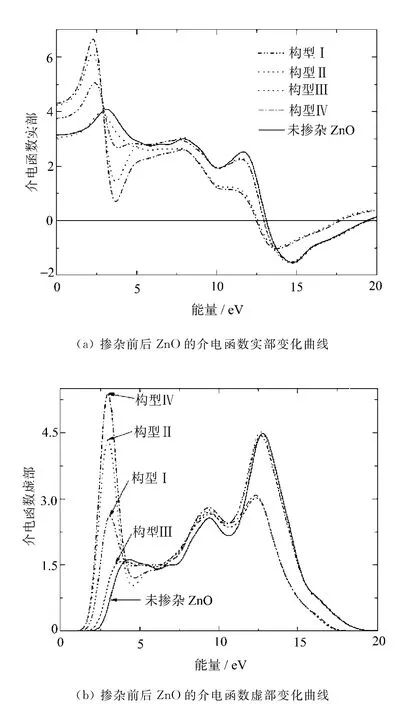
图5 随光子能量变化曲线
图5(a),(b)分别给出掺杂前后ZnO的介电函数实部与虚部随光子能量变化的曲线。通过介电函数能够探究材料的电子结构及它的光学性质,揭示载流子在带间跃迁的物理过程。介电函数实部与虚部的变化不完全独立,利用克喇末-克朗尼格(KK)微分关系可以从介电函数的虚部得到实部。
在图5(a)中,可以看到介电函数实部曲线与实轴两次相交。未掺杂ZnO的静态介电常数ε0为3.1,掺杂N,Ga后,构型Ⅱ,Ⅳ静态介电常数ε0分别增加至4.2和4.3,构型Ⅰ增加到3.8,而构型Ⅲ几乎没变,这是由于掺杂导致带隙收缩造成静态介电常数增大。
介电函数虚部色散曲线与材料对光的吸收有关。在图5(b)中,未掺杂ZnO介电函数虚部具有3个介电峰,其中位于4.32eV附近的峰来自O 2p与 Zn 4s轨道间的直接跃迁;而位于9.38eV附近的第二个峰对应Zn 3d到O 2p态的带间跃迁;而12.79eV附近的峰则来自O 2s态到Zn 3d态的带间跃迁,这与Sun J[8]等的计算结果是一致的。
掺杂后介电函数虚部依然为3个介电峰,其中构型Ⅰ,Ⅱ,Ⅳ的峰位于2.96eV附近,构型Ⅲ的峰位于3.87eV附近,我们分析后认为,这些峰来自于受主杂质能级向导带的跃迁和O 2p与Zn 4s带间直接跃迁的叠加,相比未掺杂ZnO的4.32eV附近的峰,均向低能方向移动,由于掺杂,费米能级进入价带,禁带中出现杂质能级,为电子与光子耦合提供“台阶”[9],而且由于掺杂浓度较大,引起带隙收缩,相应的电子从价带跃迁到导带所需能量减小,介电函数虚部的吸收边均发生红移。掺杂前后位于9.38eV处对应O 2p到Zn 3d态间的带间跃迁的峰几乎没变。
3 结 语
1)4种掺杂构型均引起能带简并度降低,能带劈裂,带隙收缩,并在禁带中引入受主杂质能级,构型Ⅲ,Ⅳ费米能级更加深入价带,费米能级附近出现部分占据杂质能级,可以作为P型导电材料。
2)在光学性质方面,由于引入N,Ga杂质,使得ZnO材料的介电常数增大,对可见光的吸收增加。
3)由于4种掺杂在可见光区的吸收系数不同,可以作为实验上制备N,Ga共掺杂ZnO材料时,判断形成哪种N,Ga结构的一个判据。
[1]陈琨,范广涵,章勇,等.In-N共掺杂ZnO第一性原理计算[J].物理学报,2007,57(5):3138-3147.
[2]张金奎,邓胜华,金慧,等.ZnO电子结构和p型传导特性的第一性原理研究[J].物理学报,2006,56(9):5371-5375.
[3]赵慧芳,曹全喜,李建涛.N,Ga共掺杂实现p型ZnO的第一性原理研究[J].物理学报,2007,57(9):5828-5832.
[4]刘建军.掺Ga对ZnO电子态密度和光学性质的影响[J].物理学报,2009,59(9):6466-6472.
[5]Decremps F,Datchi F,Saitta A M,et al.Local structure of condensed zinc oxide[J].Phys.Rew.B.,2003,68:104101.
[6]Fumiyasu Oba,Atsushi Togo,Isao Tanaka.Defectenergetics in ZnO:A hybrid Hartree-Fock density functional study[J].Phys.Rew.B.2008,77:245202.
[7]黄丹,邵元智,陈弟虎,等.纤锌矿结构Zn1-xMgxO电子结构及吸收光谱的第一性原理研究[J].物理学报,2008,57(2):1078-1083.
[8]Sun J,Wang H T,He J L,et al.Ab initio investigations of optical properties of the high-pressure phases of ZnO[J].Phys.Rev.B.,2005,71:125132.
[9]徐凌,唐超群,钱俊.C掺杂锐钛矿相TiO2吸收光谱的第一性原理研究[J].物理学报,2010,59(4):2721-2727.

