反舰导弹自控终点散布分析

李焱明，郜 鹏，孙 鳌，梁 琦，林慧桢

(中国人民解放军第4328工厂光电研究所，山西长治 046011)

0 引言

导弹武器系统精度是导弹武器系统的重要技术指标，也是导弹武器系统评定的重要内容之一。导弹武器系统精度分析的任务就是确定具有代表性的精度指标，分析影响精度的各个误差因素，进而科学地进行试验分析，运用统计理论完成精度评定。

反舰导弹精度一般指导弹的射击精度，它是射击精确度的简称，它的概念包括射击准确度和射击散步度两个部分。反舰导弹的射击精度，可以用单发导弹在无故障飞行条件下命中目标的概率来表示。

由于设备误差、零漂及各种干扰的随机性，在讨论射击精度问题时，通常选取弹道特征点为分析计算的依据。对于自控加自导控制体制的飞航导弹，特征点通常选在自控飞行终点和命中点。因此，对于反舰导弹研究自控终点散布和命中点散步是精度分析的主要任务，以下重点对反舰导弹的自控终点的散布进行分析［1］。

1 自控终点散布分析

导弹的实际弹着点相对散布中心的离散程度称为散步度，通常用随即变量的标准差或均方根偏差来表示。所谓自控终点，即是末制导雷达开机时导弹所在的位置。自控终点(偏差)散布，即是实际飞行弹道的自控终点与理论的自控终点的偏差。这个偏差直接影响末制导雷达开机后对目标的捕捉概率。由于在自控段弹道均处于平稳飞行(无故障情况)，因此把自控终点(偏差)散布分为侧向散布和纵向散布。

1.1 自控终点侧向散布分析

(1)火控系统输出射击诸元误差引起的自控终点散布

导弹在实施射击之前，火控系统设备要进行一系列工作:来自目标探测系统的目标运动参数不断提供给射击指挥仪，由其进行射击诸元的计算和装定。这个工作过程的每一个环节，无论是测量、计算和装定都存在设备误差。计算和装定参数都是服从一定分布的随机变量，因而射击诸元误差将使导弹在自控终点产生侧向散布［2］。

通常火控系统造成的自控终点散布可用下式表示:

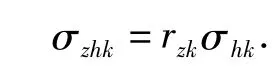
式中:rzk—自控飞行距离;

σhk—由火控系统误差而引起的自控终点散布标准差。

(2)飞行控制误差引起的自控终点散布

导弹发射后，理论上讲应沿着预先瞄准的战斗航向飞行，有自动驾驶仪进行自主控制的导弹，战斗航向由自由陀螺仪的oxth轴决定。在飞行过程中，oxth轴并非是始终保持不变的，由于陀螺漂移，实际上oxth轴是在开锁位置随机变化的。这种变化相当于射向基准轴本身发生的变化，是弹上航向陀螺所无法避免的。它对导弹自控终点所造成的侧向散布，一般可由下式确定:

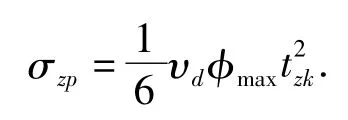
式中:υd—导弹的巡航速度;

φmax—航向陀螺最大漂移速度;

tzk—自控飞行时间。

为克服常值干扰，在自动驾驶仪中设计了积分机构。它一般都有一段非灵敏区，在非灵敏区内即使由于干扰引起航向姿态变化，积分机构也不能敏感，以致无法产生控制信号去消除干扰对飞行姿态的影响，它引起的自控终点的航向分布为:

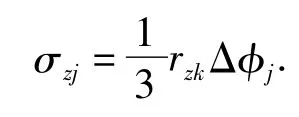
式中:Δφj—积分机构非灵敏区;

tzk—自控飞行距离。

(3)航向姿态角误差Δφ引起的自控终点散布

航向姿态角误差Δφ对自控终点散布的影响机理是:导弹沿理论弹道飞行至自控终点时导引头开机，此时导弹纵轴应与目标瞄准线(目标与导弹的连线)重合。由于各种干扰及导弹本身误差的影响，弹轴与目标瞄准线是不可能重合的，即存在一夹角Δφ。它对导弹捕捉目标的影响可折算成侧向散布，认为导弹纵轴ox1与目标瞄准线平行。这样处理同该夹角对导弹捕捉目标的影响是完全等效的。因此有:

σzΔφ=rzdσΔφ.

式中:rzd—装定自导距离;

σΔφ—姿态角散布标准差。

以某型空舰导弹为例，姿态角散布标准差是由以下误差综合而成。定向误差(战斗射向的初始偏差)，它包括指挥仪计算扇面发射角误差ε1;航向陀螺开锁误差 ε2;结构安装偏差(弹轴—载机轴的安装误差)ε3;前置角装定误差ε4;航向电位计零位误差ε5;自由陀螺漂移误差ε6;积分机构非灵敏区误差ε7。且

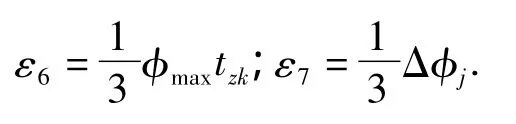
由航向姿态误差所引起的自控终点散布σzΔφ为:

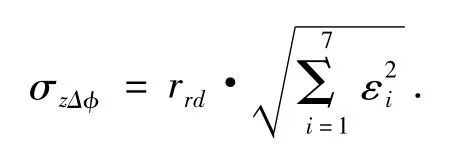
(4)目标机动修正误差所引起的自控终点散布

导弹火控系统计算射击诸元时，一般假设目标作匀速直线运动，而实际情况是，在导弹飞行过程中，目标在发现导弹后，除采用其他手段对导弹实施干扰和抗击，使之丧失战斗力之外，还可以用改变航速航向等机动运动方式“摆脱”导弹的跟踪，也就是说目标不作典型的匀速直线运动，尤其在受到速度低、飞行时间长的飞航导弹的攻击时，目标实施机动性的可能性更大。由目标机动产生的射击诸元计算误差难以估计。作为一种补偿，在指挥仪的计算公式中对目标的运动速度用修正系数κ加以修正，即以κVm作为参数Vm的输入值。在计算目标机动所造成的自控终点误差σzm时，采用Δκ作为系数κ值的修正误差。

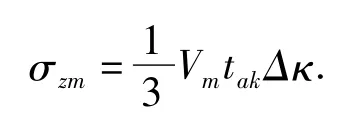
(5)大气干扰引起的误差所引起的自控终点散布

大气干扰主要指的是风，包括风速、风向及大气温度等对导弹飞行的影响，尤其是风对导弹的飞行精度影响更为明显。为了减小风对自控终点散布的影响，目前已研制成功的几种飞航导弹都采用了不同技术途径对风的影响做了修正，空舰导弹采用纵向射程控制和侧向航迹控制，力图消除风对飞行误差的影响，采用惯导对消除风的影响是非常有效的。应该说明的是，即便采取了上述的各种技术措施，由于控制系统敏感部件的测量精度有限，以及风的装定数据与实际风场间存在差异，风对自控终点造成的散布是必然存在的，但这种散布可以被大大减少。对自控段进行航向姿态稳定的飞航导弹，在射前已经对侧风的影响作了修正，但是由于测定风速、风向有误差和风随时间而变化，修正后的误差仍是不可避免的，假定侧风与实际侧风的标准差为σf，则由于修正不准所造成的侧向散布为:

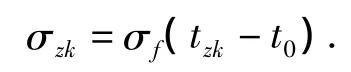
式中:tzk—导弹自控飞行时间;

t0—时间常数，可预先确定。

综合上述，导弹侧向总散布

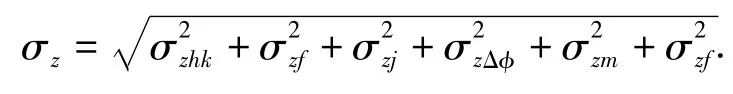
1.2 自控终点纵向散布分析

以某型空舰飞航导弹为例，纵向控制方案为射程多普勒雷达自主控制，它的控制过程简要叙述如下:导弹火控系统根据目标信息及弹道方案计算出导弹的自控飞行距离rzk并将其装定到指令计算机中，在导弹发射后的自控飞行过程，多普勒雷达不断测算出导弹的实际地速υg，并以电信号形式将它传送到指令计算机中积分，从而得出导弹的飞行距离xg，指令计算机将装定的 rzk与计算得到的 xg实时进行比较，当满足条件xg=rzk－4vd时，多普勒雷达开机，由指令计算机发出弹上末制导雷达开机指令Z3，从而结束了自控工作状态，转入自导工作状态。

根据射程控制方案，对纵向自控终点散布进行分析，找出以下几种主要误差因素:

(1)火控系统计算自控飞行距离误差(σxhk)

由火控系统计算并装定到指令计算机内的自控飞行距离是末制导雷达开机的基准距离，其精度的高低对自控终点散布的影响较大，在设计阶段，在一定条件下，火控系统的自控距离精度可利用射击命中方程的解析方法或统计试验法求得，也可通过火控系统的精度试验获得。

(2)多普勒雷达对导弹飞行距离的测算误差(σxd)

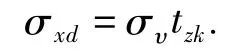
式中:συ—多普勒雷达测地速误差。

(3)指令计算机发出末制导雷达指令“Z3”时的距离误差(σxzl)

根据要求，指令计算机发出“Z3”时的最大距离误差

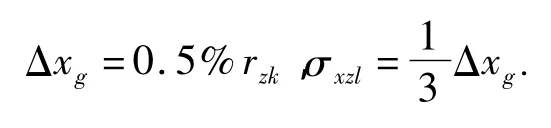
(4)目标机动修正误差(σxm)

此项误差对纵向自控终点散布的影响与对侧向散布的影响相似，即有:

(5)导弹在飞行过程中受到干扰后所形成的自控终点误差(σxΔt)［3］

设装定的自控飞行距离为rzk，与其对应的自控飞行时间为tzk，由于飞行中受到弹上设备误差例如自由陀螺漂移，以及发动机的推力偏差等因素的影响，将在自控终点产生距离散布，因此，当满足开机条件xg=r′zk时，导弹实际飞行时间 t′zk与理论开机时间 tzk不等，设 Δtzk=tzk－t′zk.

对于运动目标，Δtzk的偏差将使目标相对预定瞄准点产

生射程上的偏差。

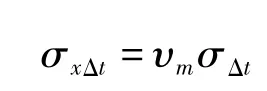
式中:υm—目标运动速度;

σΔt—时间偏差Δtzk的均方差。

飞航导弹采用纵向射程控制方案后，与通常采用的时间控制方案相比较，导弹在自控终点距离上的散布可以减小，对于时间控制方案的导弹，由Δtzk引起的自控终点散布用下式表示:

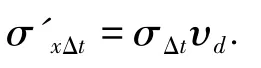
若取 υm=20 m/s，υd=306 m/s.

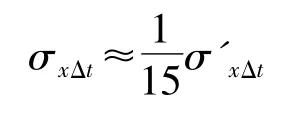
(6)纵风对自控终点散布的影响σxf

风对导弹的运动有很大的影响，在弹道计算中一般都是用设定的常值来进行修正。对于射程控制的飞航导弹，纵风对自控终点散布的影响机理与自控终点侧向散布分析相同。

综上所述，导弹自控终点的纵向总散布为:

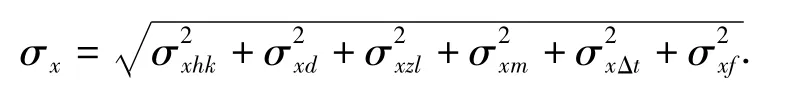
2 结束语

对反舰导弹的侧向散布和纵向散布进行分析，可比较准确地知道末制导雷达开机时导弹所处的位置，可大大提高反舰导弹的射击精度，进而会影响反舰导弹在作战中的射击精确度。

［1］曲宝忠，孙晓峰.海军战术导弹试验与鉴定［M］.北京:国防工业出版社，2005.

［2］［美］艾希布拉特.战术导弹的试验与鉴定［M］.蔡道济，等译校.北京:国防工业出版社，1992.

［3］方有培.反舰导弹及舰艇的干扰、隐身技术［J］.航天电子对抗，2000(3):5－9.