关于连续性和离散性概念*

李宏德

(河南机电高等专科学校，河南 新乡 453000)

连续性和离散性是自然科学发展史上两个重要概念，其中离散性似乎更具色彩，无时不闪现自己的身形，即使在那些特别钟爱连续性的情况下也往往会把离散性概念重重地提上几笔。当然这并不排斥连续性的重要。也正是这种各概念在不同时期、不同领域的不平衡性发展及在各种不同现象下的主次矛盾才使得物理学的各个分支都显得丰富多彩，而且在研究方法上更是各得所需。以简洁、准确、实用为原则，我们有时可能感觉到连续性和离散性这两个概念是矛盾的、对立的，可我们又不得不认为它们间在细微之处得到很好的统一(矛盾也常常是在这里显露)。但对这两个概念关系的讨论很大程度上是借助于数学工具。当然这里并不是说这两个概念已经发展得很完善了，相反，其不足之处也是显而易见的，就目前而言，连续性和离散性概念还没有给出严格的定义，它们是否能精确描述?现在的数学上和实验上的描述方法是否有问题?

现在我们来简单回顾一下这两个概念的发展过程，物理实体(包括场)都是由微观粒子组成的论断已为众多物理学家所接受，物体具有微观结构，基本粒子不基本，场也是具有微观性质的，尽管引力场尚待研究。但目前光作为电磁场的一部分知其是由光量子组成，而且光子和场相互作用，这是上述结论的一个证明。因此我们就不得不承认物理实体在宏观上的连续性和微观上的离散性。

经典力学整体而言是研究离散质量的问题，当经典力学具体应用到工程中去，要了解整个物体的全面角色时，产生了连续性要求。在数学上由于变数的产生也有了连续性要求，至于说是物理应用于工程而推动了数学，还是数学带动了物理或是两者平行发展这些问题的讨论更具有哲学色彩。但值得注意是，就工程物理来说连续性概念的产生恰恰是由于深入研究离散性问题的结果，即当我们要研究物体整体属性时就有必要把物体化为各个单元，先研究单元特征然后综合成总体特征(相似于有限元方法。以有限元法为代表的一系列离散化数值方法的提出在力学学科领域里引起了变革［1］)，这样就从离散性的基础上导出连续性来。认识到这一点或许是重要的，现代物理学的统计方法也正是这一思想的发展。牛顿－莱布尼茨从变数引出微积分，使统计算法有了强有力的工具，波尔兹曼进而提出了统计计算思想。统计方法在研究气体分子运动中已经得到很好的应用，使我们通过对微观现象的研究更清楚地理解宏观问题。

连续性和离散性概念是等价的还是有一个作为最基本的呢?是否可以注意这样一个现象，要想清楚地理解宏观现象我们就有必要去详尽地研究其微观现象，而且微观现象的统计结果常常会引发宏观理论的更高突破，也更精确。量子力学与经典力学的比较似乎可以说明些什么。

在数学工具上，微积分的创立使得统计计算成为可能，使微观研究成果更容易延伸到宏观领域，而相反的过程却难以实现。

微观现象的研究会使问题走向深入，更接近真实。连续性概念可以看做离散性概念下统计分析的结果。

流体连续介质模型是建立在统计的基础上的，引入一个具有特殊地位的物理量——流体质点，可以把它看做一个离散的点，但它本身仍然保持着连续性，这样一个双重身份的量，在概念的过渡和理解上都是必要的。

所以说它仍保持有连续性，是因为它有一个特殊的特征——体积△V'。看做是几何尺寸很小，但又包含足够多的分子的体积。在此体积内，流体的宏观特征就是其中分子的统计平均特征，而且把流体质点定义为微元体积△V'中所有分子的总体。

需要注意的是流体质点的离散性。△V'中流体平均密度定义为

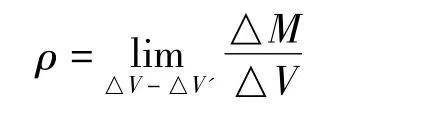
这是把△V'这个不可逾越的体积下限看做一个特殊的质点，即强调了它的粒子性，并把流体定义为连续分布的流体质点所组成。可以看出流体连续介质模型是建立在离散性统计平均基础上的，同时也应该注意到它的相对性。

［1］龙驭球.有限元法概论［M］.北京:人民教育出版社，1981.

［2］W·海森堡.物理学与哲学［M］.范岱年译.北京:科学出版社，1974.

［3］［德］康德.宇宙发展史概论［M］.上海外国自然科学哲学著作编译组译.上海:上海人民出版社，1973.

［4］杨建邺，止戈.杰出物理学家的失误［M］.武昌:华中师范大学出版社，1986.

［5］王福山主编.近代物理学史研究［M］.上海:复旦大学出版社，1983.