层次分析法在土料场选择中的应用

康迎宾，康 鹏，张战强，宋劲草

（1.华北水利水电学院，河南郑州 450011；2.洛阳市水利工程局，河南洛阳 471000）

土石料是水库除险加固工程的主要建筑材料，而料场的合理规划和使用是土石坝施工中的关键技术之一，是缩短工程建设工期、降低建设费用、保证施工质量的关键因素，而料场位置的选择直接关系到施工总体布置格局。因此，在进入可行性研究和招标设计阶段后，对料场选择应持特别重视的态度，进行了多方面研究。

1 工程概况

洛阳市龙脖水库位于洛河支流连昌河中游，坐落在河南省陕县李村乡龙脖村，水库控制流域面积211 km2，设计灌溉面积0.43万ha。工程1959年冬天开工建设，1973年建成，前后历时15 a，形成现在规模，是一座具有灌溉、防洪、养殖等综合效益的中型水库。水库建设于上世纪50年代，属于“三边”工程，工程运用至今，设备陈旧老化，建筑物多处存在工程隐患，水库带病运行，运行中发现许多问题亟待解决，安全鉴定其为三类坝。

在龙脖水库除险加固工程中，所需天然建筑材料有土料、砂石料、块石料三种，其中土料需求量为1.5万m3。库区周边分布着众多土料场，因此需要对其进行优化选择，以满足工程的需要。

考虑加固施工过程中料场对于工程建设的重要性，保证工程费用最低，兼顾施工环境、水土保持以及生态环境等要求，基于这几方面的考虑既有常规的经济、技术等定量性指标，也有环境保护等定性指标，对于定量指标与定性指标相结合的问题，常规的优化方法难于处理，故采用层次分析法。

2 层次分析法

人们在对社会、经济等领域问题进行系统分析时，面临的常常是一个由相互关联又彼此制约的众多因素构成的复杂而又缺少定量数据的系统。在做评价决策的时候，许多要考虑因素的优先程度往往难以量化，人的主观选择会起着相当重要的作用，这就给用一般的数学方法解决问题带来了本质上的困难［1］。

层次分析法（Analytic Hierarchy Process，简称AHP）的提出为解决这类较为复杂的问题提供了简洁而实用的方法。它是美国运筹学家T.L.Saaty教授于上世纪70年代初期提出的一种多准则决策方法。它在处理复杂的决策问题时，将问题层次化，分解为不同的层次结构，从而对方案层各要素进行优劣等级排序，最终选择最优方案，为决策者提供了可靠的理论依据。

运用层次分析法建模，大体上可按下面四个步骤进行[2-5]：

（1）建立层次结构模型。首先将深入分析的实际问题层次化，将复杂问题分解为多个元素的组成部分，按其属性及关系分解为不同的层次结构，构造出一个有层次的结构模型。上一层次的各要素对与其相邻的下一层次各从属要素起支配作用。

最高层：这一层中只有一个元素，称为目标层。

中间层：由若干个层次组成，包含了为实现目标所要考虑的各种准则，又称为准则层。

最底层：这一层包括可供选择的各种决策方案，称为方案层。

（2）构造出各层次中所有的比较矩阵。将层次结构模型的准则层、方案层中各要素对于其从属于的上一层要素，构造成比较矩阵。例如：

式中：aij表示元素i和元素j相对于上一层某一元素进行比较时，i比j的相对重要程度，采用1～9的比例尺度法。其比例尺度及含义如表1所示。

表1 判断矩阵的比例尺度及其含义Table 1:Ratio and its meaning in the judgment matrix

（3）计算权向量并做一致性检验。计算每一个比较矩阵的特征向量来决定下一层次各要素对上一层次某一要素的权重，并验证其是否通过一致性检验。

①计算权向量：

将矩阵A的列向量归一化：

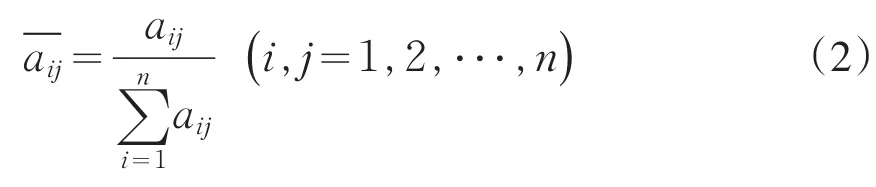
求归一化处理后的矩阵各行元素之和：

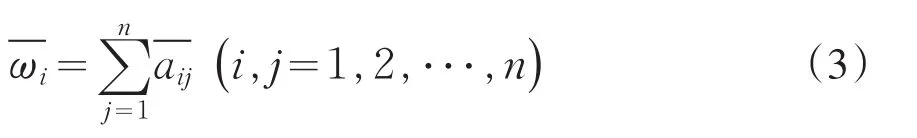
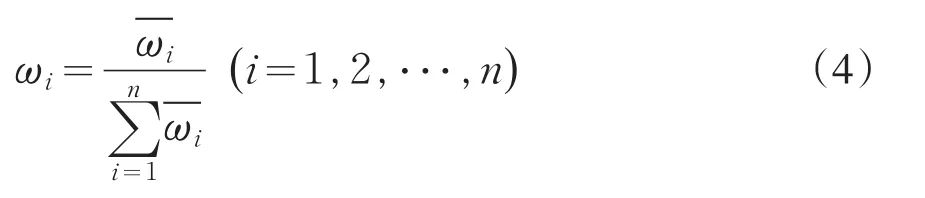
则ω=(ω1,ω2,⋅⋅⋅,ωn)T即为所求的权向量，且ω1+ω2+⋅⋅⋅+ωn=1

②一致性检验

计算λmax作为矩阵A的近似最大特征值：

计算一致性指标CI：

根据表2可查出相应阶数的随机一致性指标RI。

计算一致性比率CR：

当CR＜0.1时，认为矩阵A的不一致程度在允许范围以内，否则须对矩阵A进行调整使其满足CR＜0.1。

（4）计算组合权向量并做组合一致性检验。计算结构模型的组合权向量，求出方案层各要素对目标层的权重，对方案层各要素进行优劣等级排序，并检验其一致性。

当方案层对目标层的组合一致性比率CR＜0.1时，认为整个层次的比较判断通过一致性检验。

考虑到求解比较矩阵的特征向量和特征值等各项指标时，计算繁琐且不精确，为此运用Matlab计算软件进行计算，可以保证计算结果的准确性。采用此软件只要输入比较矩阵和相应的命令就可以得到各比较矩阵的权向量、方案层对目标层的组合权向量及其一致性比率等。

表2 随机一致性指标RI的数值Table 2:Values of the random consistency index RI

3 案例应用

在龙脖水库除险加固工程中，土料需求量为1.5万m3，周边主要有王营、张沟、塔罗以及王彦等土料场，因此通过层次分析法对上述料场进行优化选择，以满足工程的需要。

3.1 层次结构模型

对建筑材料土料进行选择时，在保证质量的前提下，要充分考虑诸如土料的储量、运距、开采费用以及环境保护等因素。储量问题关系到能否满足除险加固工程对土料的需求量，运距主要考虑运输的距离、运输的难易程度等，开采费用主要指剥离层的厚度、开采的难易程度等，直接关系到工程预算，而环境保护则是体现可持续发展的一个重要指标。建立层次结构模型见图1。

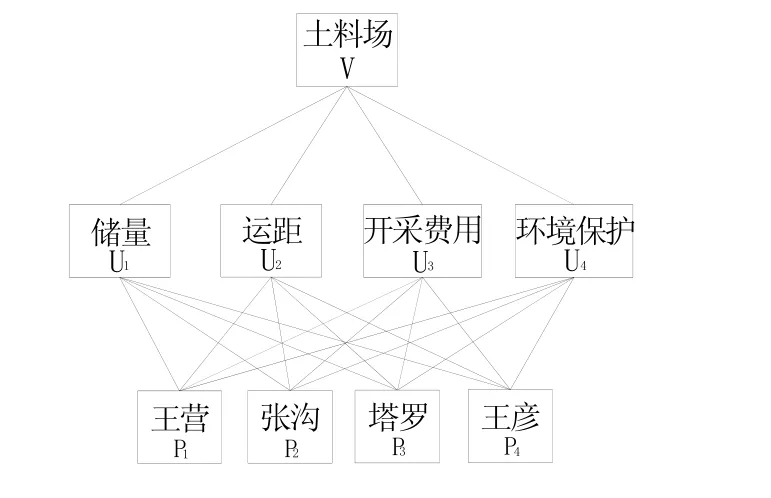
图1 层次结构模型Fig.1 Hierarchical structure model

3.2 比较矩阵的构造及相关计算

料场选择要满足工程经济预算、工期、工程质量和环境保护等方面的要求，通过业主单位和施工单位有关专家评定，对准则层的上述四个指标（即经济预算、工期、工程质量和环境保护）相对于土料场的重要性进行两两比较，构造出比较矩阵，并计算出其权重，计算结果见表3。

储量问题关系到能否满足除险加固工程对土料的需求，王营、张沟、塔罗、王彦料场的土料储量分别为 2.1 万 m3、3.4 万 m3、2.8 万 m3、4.2 万 m3。王彦土料场的料源储量尤为明显。建立比较矩阵见表4。

运距与包括运输的距离、畅通情况等在内的许多因素有关。王营位于坝体右岸东北方向，距坝肩1 km；张沟位于坝体下游以南方向的山岭上，距坝肩1.4 km；塔罗位于左坝肩北偏西方向，距坝肩2.8 km；王彦位于坝左岸以南山岭上，距坝趾2 km。在土料场的选择中，王彦、塔罗土料场距公路近，地势平坦，运输较方便；而王营、张沟土料场运输较不方便。建立比较矩阵见表5。

表3 土料场的比较矩阵V-U及权重Table 3:Comparison matrix of the soil yards V-U and weights

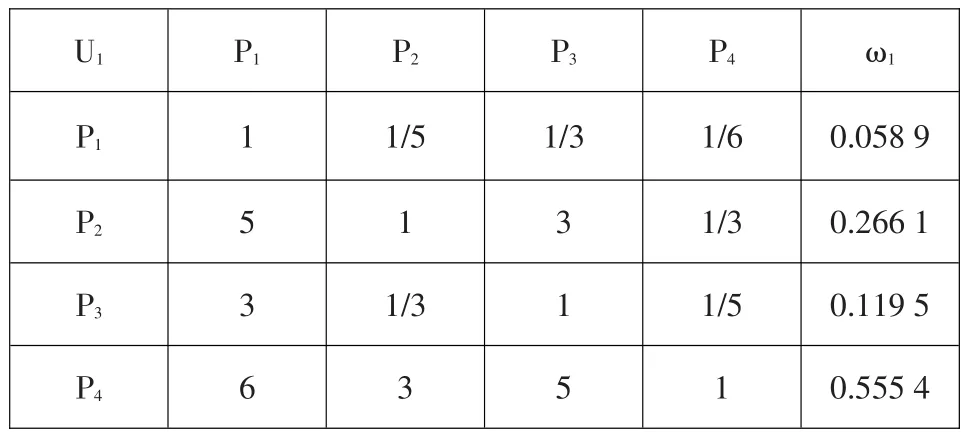
表4 储量的比较矩阵及权重Table 4:Comparison matrix of the reserves and weights

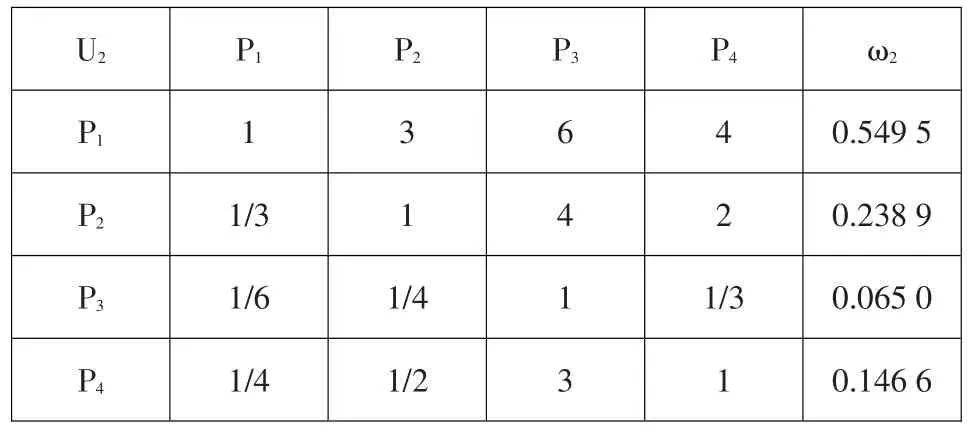
表5 运距的比较矩阵及权重Table 5:Comparison matrix of transport distances and weights

开采费用直接关系到工程预算，包括开挖的难易程度、剥离覆盖层的费用、弃渣处理的费用等。王营料场高程在640～650 m之间，表层为腐殖土，厚度1 m；张沟料场高程在647～660 m之间，表层腐殖土厚0.8 m；塔罗料场高程在630～645 m，岩性为低液限粘土，表层腐殖土厚度1.3 m；王彦料场高程593～607 m，上覆耕植层厚约0.5 m。建立比较矩阵见表6。

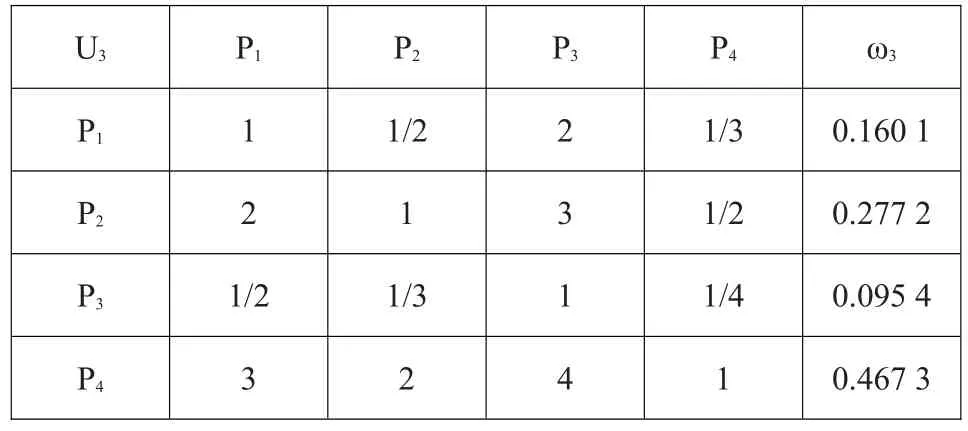
表6 开采费用的比较矩阵及权重Table 6:Comparison matrix of exploitation costs and weights

环境保护是体现可持续发展的一个参照指标，土料场开挖考虑的环境保护主要是覆盖层剥离产生固体废弃物等弃渣、后期的覆土、林地恢复防止水土流失等。建立比较矩阵见表7。

表7 环境保护的比较矩阵及权重Table 7:Comparison matrix of environmental protection and weights

以上准则层各比较矩阵的一致性比率CR的计算结果均小于0.1，满足一致性检验，各ω值可作为权向量。

3.3 组合权向量及一致性检验

方案层的四个方案相对于目标层土料场的组合权向量计算及一致性比率结果见表8。

从表8的组合权向量可以看出，王营、张沟、塔罗、王彦四个土料场对总目标的权重值分别为0.162 6、0.252 8、0.133 1、0.451 5，其中第四个方案王彦料场在料场选择中占的比重为45.15%，远远大于第一、二、三方案的比重，所以最能满足对土料的需求，选择该料场最为合适。

组合一致性检验：由Matlab计算程序得出CR=0.076 7＜0.1，通过了组合一致性检验，上述组合权向量计算结果可以作为最终决策的依据。

4 结 语

水库除险加固工程的土料场选择受土料储量、开采费用、运距、环境保护等多种条件制约，在这些因素中既有储量、开采费用、运距等可以定量的指标，又有环境保护等只能定性难以量化的指标。将系统的、层次化的、定性和定量相结合的分析方法——层次分析法引入到各项指标权重的确定中来，同时经过有关专家评定，从而大大减小了人的主观因素的影响，最终选择既满足工程施工需要又经济合理的料场方案，保证了决策的客观性、科学性和合理性，为决策者提供了非常有参考价值的依据。

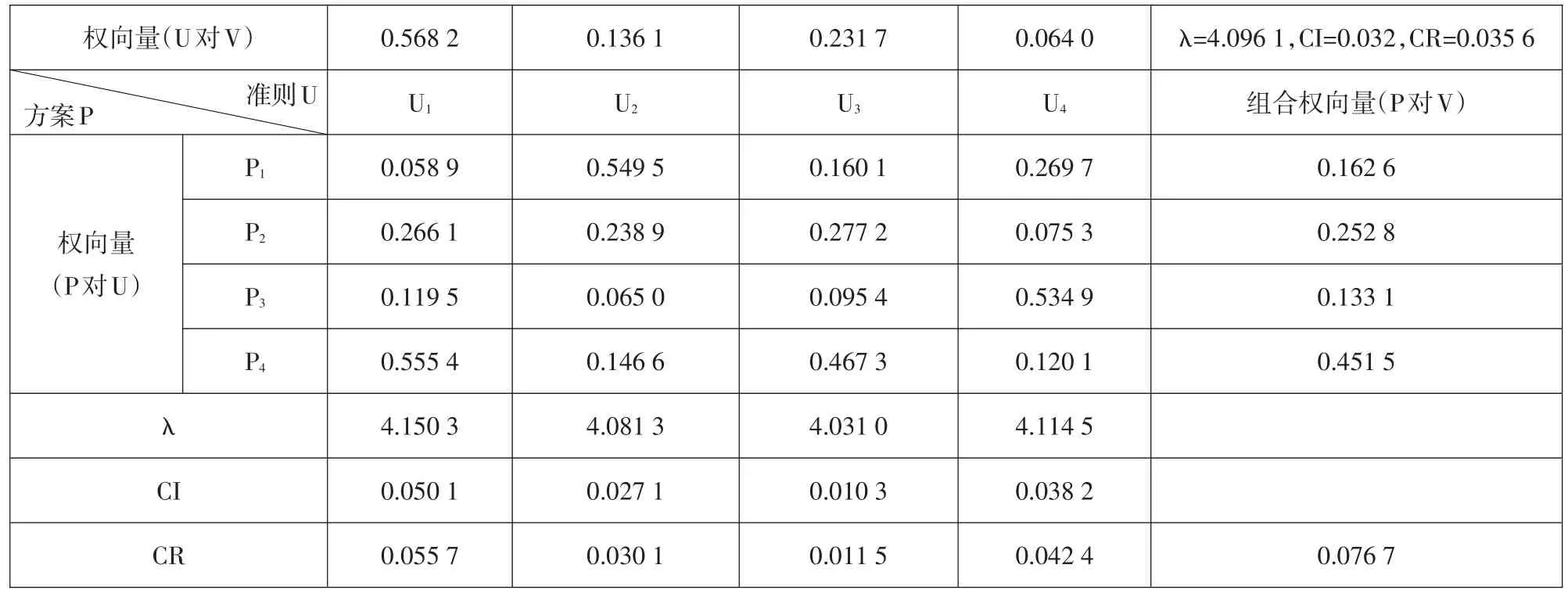
表8 以土料场V为目标的计算结果Table 8:Calculation results of the soil field V

[1]姜启源.数学模型[M].北京:高等教育出版社,1993.

[2]李晓东,曾光明,梁婕.基于层次分析法的洞庭湖健康评价[J].人民长江,2009,40(14):22-25.

[3]杨波,唐德善,卢兴旺.基于AHP的河道整治方案优选[J].水电能源科学,2010,28(2):109-110.

[4]张笃涛,郭天虎,董振旗.层次分析法在军事风险投资项目中的应用[J].中国西部科技,2009,8(19):23-24.

[5]王力平.模糊层次分析法在实际工程中的应用[J].山西建筑,2009,35(23):209-210.