基于虚拟磁链的风力发电并网变流器直接功率控制研究
马 晓娜 ,任 一峰
(中北大学信息与通信工程学院,太原 030051)
0 引言
在可再生能源开发利用的风力发电技术中,一种交流励磁变速恒频双馈发电系统正在得到广泛应用[1-2],其发电机的励磁变频器应具有良好的输入、输出特性,同时还必须有功率双向流动的能力,因而常采用PWM整流。经过多年发展,三相电压型PWM整流器的控制方法已经从最初的直接电流控制发展到基于旋转坐标变换理论的定向控制方法,近些年又研究出了基于虚拟磁链的控制方法[3]。引入的虚拟磁链无需检测电网电压,省去了交流电压传感器,同时提高了可靠性。本文对基于虚拟电网磁链直接功率控制系统进行了理论分析,并建设基于 MATLAT/Simulink 环境下的仿真模型,对系统进行仿真。
1 基于虚拟磁链直接功率控制系统理论分析
1.1 交流电机中磁链的概念
交流电机是一个非线性,多变量,强耦合的系统[4]。取三相定转子轴线如图1所示,并假设电压、电流、磁链的正方向符合右手螺旋法则,可以取到绕组磁链的表达式为:

图1 交流电机定转子ABC坐标系统
1.2 虚拟电网磁链估算
图2是PWM整流器的主电路,它与变频器供电三相交流电机定子电路有着很大的相似性。

图2 PWM整流器主电路
PWM整流器中的电网电压相当于交流电机的气隙磁场在定子绕组中产生的感应电势,电抗器的电感和电阻分别相当于电机定子绕组的漏感和电阻[5]。因此,可以将PWM整流器看成一台无限大由变频器供电、以同步转速恒速运行的、定子电阻和漏感分别为R和L的同步电机。
设三相电网电压平衡,忽略进线电抗器和线路的电阻R,则PWM整流器在α-β坐标系下的电压方程为[6]:

式中:Sa,Sb,Sc是三相桥臂开关函:Sk=0表示相应桥臂下管导通,上管关断,Sk=1为相应桥臂上管导通 ,下管关断 ;(k=a,b,c);uα,uβ,iα,iβ分别为三相电网电压和电流的α,β分量。
用式(2)直接进行电网电压估计可得到无电压传感器控制方法,但由于用到了电流的微分量,在实际控制中易放大噪声引入干扰,难以实现。
将式(2)的方程两边同时积分可得
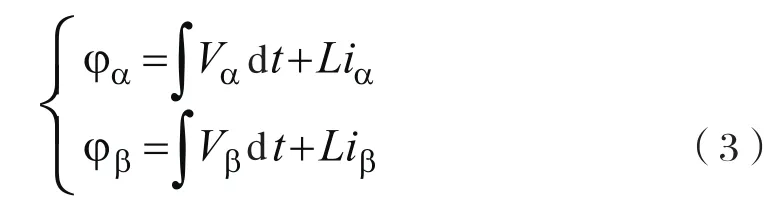
式中:Ψα,Ψβ分别为虚拟电网磁链的α,β分量。令U=uα+juβ,Ψ=Ψα+jΨβ则电网电压空间矢量U超前于虚拟电网磁链矢量Ψ电角度π/2。如图3所示,虚拟电网磁链定向的目的。实际上就是虚拟电网磁链矢量的空间位置角θ的观测。

于是θ角的观测可以转化为虚拟磁链的α,β分量的观测问题。
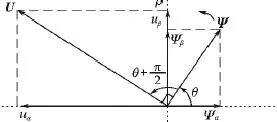
图3 三相电压型PWM整流器主电路
1.3 基于虚拟磁链的瞬时功率估算
在传统有电压传感器的直接功率控制中,通过电网电压和电流的计算获得系统瞬时功率。将虚拟磁链的概念引入到直接功率控制后,瞬时功率估算将由电流和虚拟磁链计算得出,因此可以省去交流电压传感器。
有功功率p和无功功率q的表达式为:

根据式(2),(3),(5)可得电网瞬时供给有功和无功功率分别为:
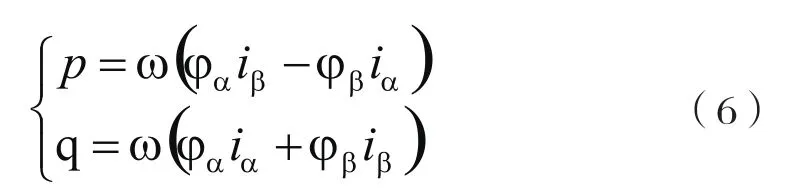
2 虚拟磁链直接功率控制系统的设计和实现
2.1 结构图
基于虚拟磁链的无电压传感器直接功率控制系统结构如图4所示。用三相桥臂的开关函数Sa,Sb,Sc及直流侧电压Vdc,再估算出瞬时有功功率P和无功功率Q,扇形划分由ψα,ψβ确定ψ的角度由于电网电压空间矢量U超前于虚拟电网磁链矢量ψ电角度π/2,所以由得到电压U的扇区信号θn,这样就实现了省去电网电压传感器的目的。

图4 基于虚拟磁链的无电压传感器矢量控制框图
2.2 积分初值问题的分析和解决
虚拟电网磁链的初始值难以用式(3)直接作积分来估算其值,否则会在估算出的虚拟电网磁链中引入与积分初值有关的直流偏置,导致坐标系中的磁链轨迹将会是一个以相应的直流偏置为圆心的圆,为了避免纯积分带来的问题,文献[7]采用惯性环节取代纯积分,观测所得磁链虽然在一定程度上解决了上述问题,但观测结果只是近似值,存在幅值和相位误差。为此,采用两个级联的惯性环节代替纯积分环节。
由于正弦信号经过纯积分之后相位滞后90。,幅值变为原来的1/ω,因此只有当两个级联惯性环节的作用效果与之相同时,才能用来取代纯积分。设惯性环节的传递函数为:
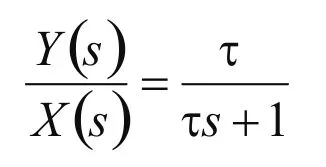
式中:X(s)为输入信号;Y(s)为输出信号;τ为惯性环节的时间常数。
该惯性环节的相位滞后Φ和幅值增益G为:
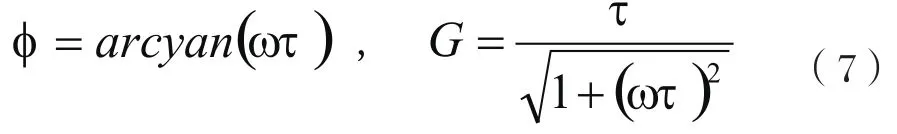
若采用两个惯性环节级联,且其时间常数相同,则级联后相位滞后Φn=2和幅值增益Gn=2可表示为:

为了得到积分效果,需要满足:
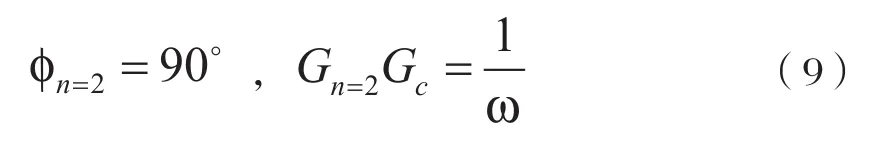
式中:Gc为对增益进行的补偿。
由以上两式可得级联型惯性环节的关键参数:

可见τ,Gc与角频率密切相关,但因电网的角频率基本不变,故采用这种级联型惯性环节实现虚拟磁链观测,无需实时计算τ和Gc,减少了计算量。
3 仿真结果
根据以上的分析,按着图4利用MATLAB/Simulink工具箱[8],建立仿真模型。为了体现系统的控制特点,对其进行了动态仿真,在0.15s的时候突增负载。仿真结果如图5(a)、(b)、(c)所示。由图5可知,(a)(b)中相电压与相电流相位差很小,基本同相位,且具有较快的的动态响应,有功和无功功率脉动较小;在负载突增工况下,电流波形具有较快的动态响应。图(c)母线电压稳定在给定值,具有较强的抗负载扰动能力。
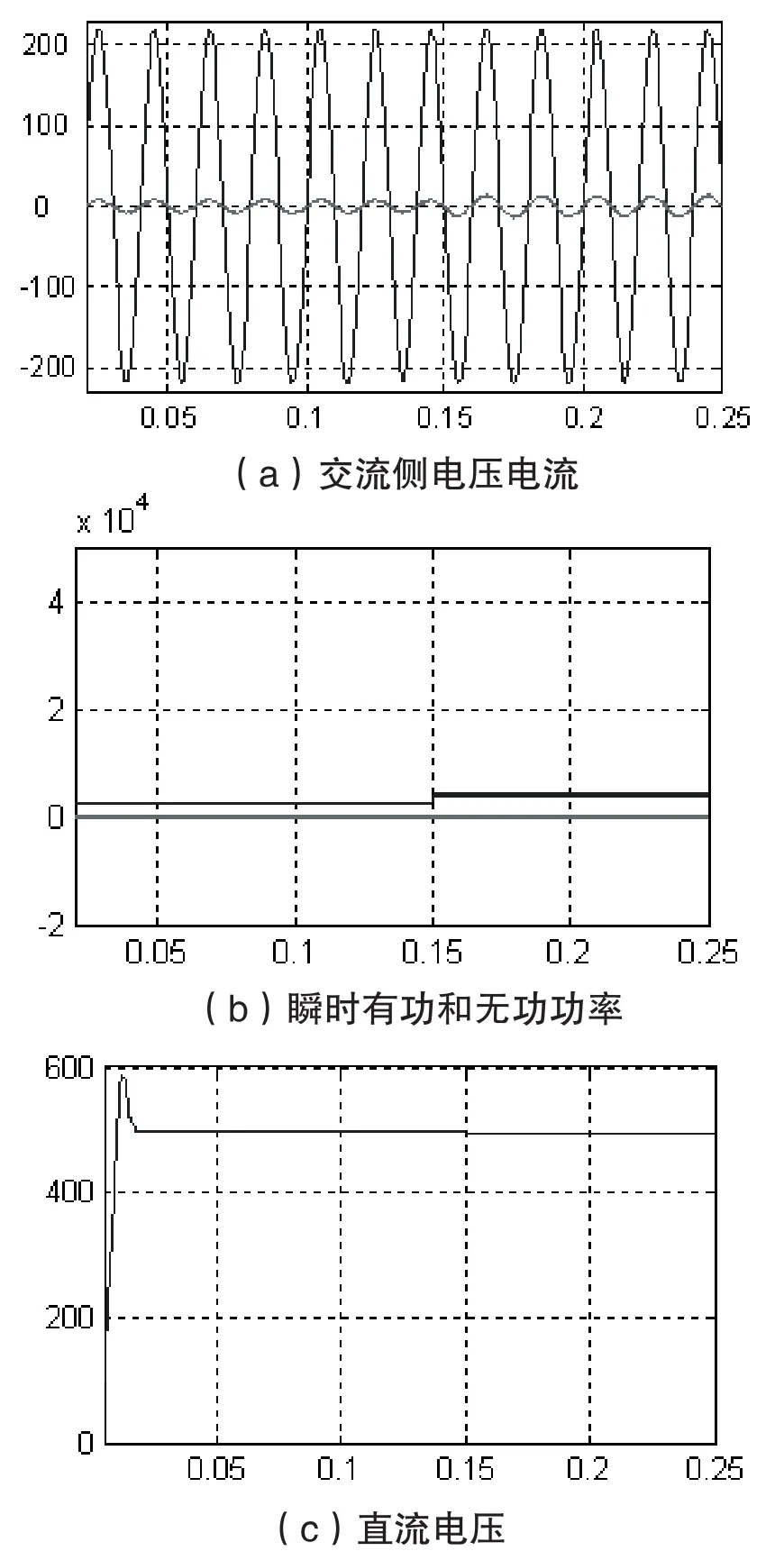
图5 虚拟磁链系统仿真波形
4 结论
仿真结果表明:基于虚拟磁链的三相PWM整流器DPC系统能与传统的DPC方法得到相同的效果,且抗干扰能力强,电网输入电流的崎变较小,具有较好的瞬时功率动、静态控制特性。并且结构简单,能有效减少传感器的数量。
[1]黄科元,贺益康.矩阵式变换器交流励磁的变速恒频风力发电系统研究[J].中国电机工程学报,2002,22(11):100-105.
[2]刘其辉,贺益康.变速恒频风力发电机空载并网控制[J].中国电机工程学报,2004,24(3):6-11.
[3]张崇巍,张兴.PWM整流器及其控制[M].北京:机械工业出版社,2003.
[4]HADIAN A S R,徐殿国,郎永强.一种PWM整流器直接功率控制方法[J].中国电机工程学报,2007,27(25):78-84.
[5]季建强.电压型PWM整流器VSR不平衡控制策略研究[D〕.合肥:合肥工业大学,2004.
[6]Malinowiski M,Mariusz SC.Sensorless Control Strategies for Three-phase PWM Rectifiers[M].Warsaw:Warsaw University of Technology,2001.
[7]赵仁德,贺益康.PWM整流器虚拟电网磁链定向矢量控制仿真研究[J].电力系统及其自动化学报,2005, 17 (5):94- 98.
[8]洪乃刚.电力电子和电力拖动控制系统的MATLAB仿真[M].北京:机械工业出版社,2006.

