基于非线性规划方法的PSS参数优化设计

董晓亮，李 江，李国庆

(东北电力大学电气工程学院，吉林吉林1320121)

电力系统稳定器(PSS)作为抑制电网低频功率振荡的重要技术手段［1-3］，是目前世界上应用最广泛、最经济且技术较为成熟的抑制低频振荡的措施。只有当PSS时间常数能对励磁系统和发电机造成的相位滞后有很好的补偿效果并且其增益恰当时，PSS才能对电网的低频振荡提供很好的阻尼。因此，其参数优化设计一直是学术和工程界的热点问题之一。至今，无论是在理论还是实践中，PSS参数整定已有众多的方法和技术。这些方法总体上分为两大类［4］，一类是现场试验法，即在机组运行中，通过测试机组及其励磁系统的开环响应特性，进而设定PSS控制参数;另一类是模型分析法，即通过机组和电网的数学模型，通过理论推导或时域仿真来设计和校验PSS参数。当然，也可将两类方法结合起来应用。PSS参数整定要使PSS的振荡阻尼作用兼顾联网后出现的区间模式(约0.2～0.7 Hz)、区内模式(约0.7～1.0 Hz)和本机模式(1.0～2.0 Hz)。而PSS参数优化数学上描述为一个非线性优化问题，通过选择合适的系统动态性能指标作为目标函数，可兼顾考虑系统多种运行方式。国内外很多学者对这一复杂的非线性优化问题作了大量研究。其中文献［5］采用的传统梯度法和文献［6］采用的遗传算法来求解PSS参数优化问题取得了一定成果。本文以河北邢台电厂的10号机组工程实际需要为目标，拟用非线性规划法(NLP)对PSS进行参数优化设计。

1 系统建模

1.1 电网拓扑

图1为系统的拓扑图，PSS以发电机的△Pout作为反馈信号从而控制励磁系统(AVR)的输出，进而控制发电机，形成一个闭环系统。

图1 电网拓扑示意图

1.2 励磁系统与PSS的模型及参数:

机组G1励磁系统AVR具有IEEE ST1A标准模型，其传递函数框图，见图2。

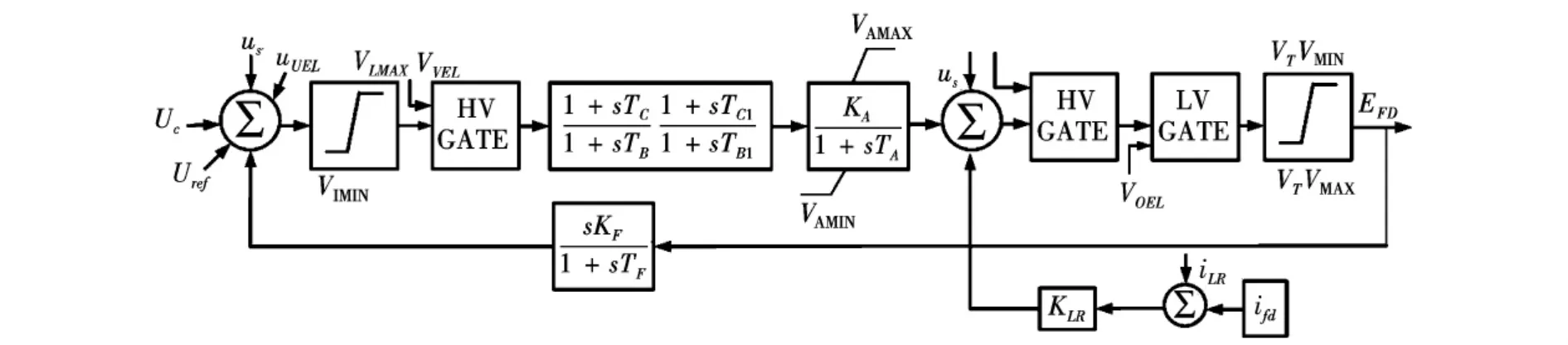
图2 IEEE ST1A静态励磁系统

AVR 的典型参数为:TC=3 s，TB=4 s，TB1=0.06 s，TC1=0.03 s，KF=0，TF=1 s，KA=56.25，TA=0.02 s。对励磁系统进行线性化分析，简化后得到AVR的传递函数如下:

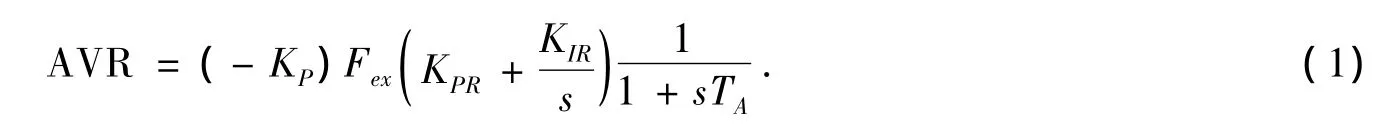
机组G1的PSS具有IEEE PSS2B标准模型，其传递函数如图3所示。

图3 IEEE PSS2B双输入电力系统稳定器

PSS 的典型参数为:Ks1=7，Ks2=6.8，Ks3=1.2，T1=0.05 s，T2=0.19 s，T3=0.05 s，T4=0.19 s，T4=0.1 s，T5=0.1 s，T10=0，T6=0.2 s，M=2，N=1，Tw1=6 s，Tw2=6 s，Tw3=6，Tw4=6 s，T7=6 s，T8=0.6 s，T9=0.09 s;其中us1代表以转速偏差作为系统的反馈量，us2代表以功率偏差作为系统的反馈量，在本例中只取功率作为系统的反馈量。可以得到其传递函数为:

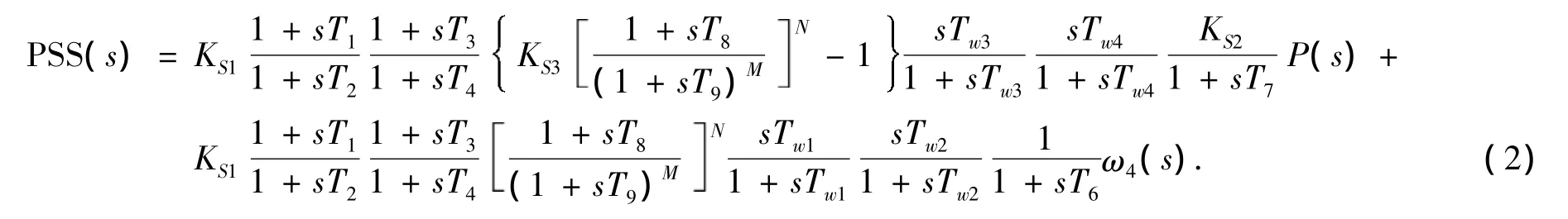
2 PSS参数优化理论

2.1 非线性优化基本理论

非线性规划(NLP)有很多解法，如可行方向、罚函数法、梯度投影法等。本文采用步二次规划法［7，8］(sequential quadratic programming，SQP)对 PSS 参数进行优化。

2.2 SQP方法的基本原理

用SQP解NLP得基本原理是:对拉格朗日函数，即

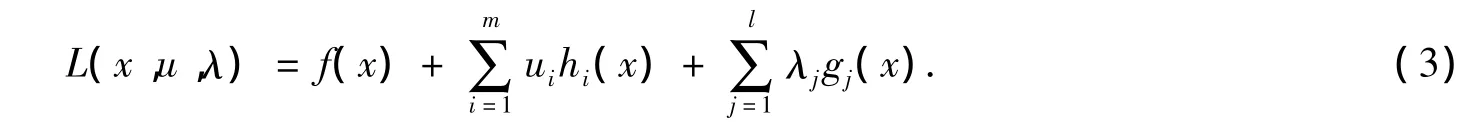
用二次函数近似L(x，u，λ)后化为QP问题，然后解一系列如下形式的QP子问题:

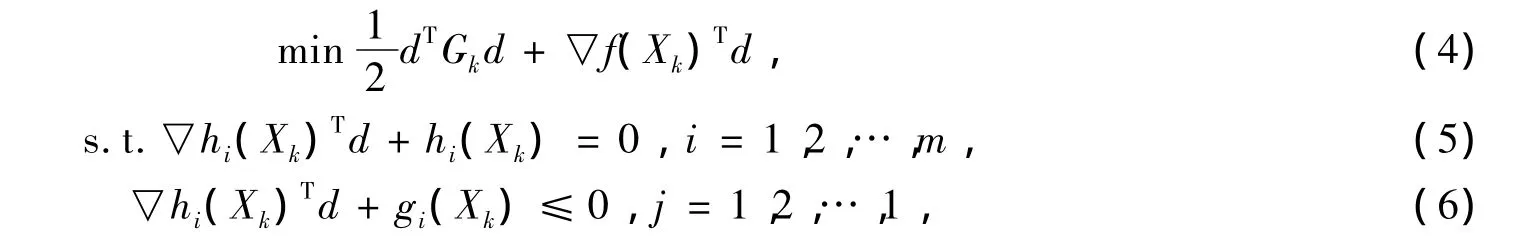
其中xk是第k次迭代的初始点;Gk是L(x，u，λ)的黑塞矩阵▽2L的近似。

由(4)式得到的最优解dk取做第K次迭代的搜索方向，新的迭代点为xk+1=xk+akdk，其中ak是按一定搜索准则得到的步长。这样，SQP包括3个主要部分:

1)求解QP子问题;

2)用线性搜索计算步长ak;

3)确定矩阵Gk的迭代公式。

2.3 目标函数及其约束调节

按照工程中要求，电力系统稳定器(PSS)通过励磁系统产生的电磁力矩在所考虑的频率范围内(0.2～2.0 Hz)与机组转速的相位差应在 ±30度范围。频率的取值为0.1～2 Hz在之间，设定步长为0.1，有M个频率点，各个点的权重为wi，yi=F(xi)为在x点的相位，使PSS中的各个参数要在一定的范围内取值。在一定频率和不同参数的作用下PSS将产生不同的相移。因此，我们把目标函数定义为

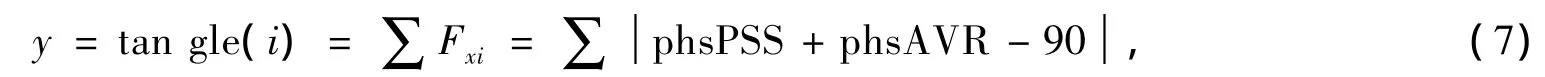
其中，tan gle(i):PSS通过励磁系统(AVR)产生的电磁力矩与机组转速的相位差;phsPSS:代表PSS产生的相移;phsAVR:代表AVR产生的相移。

将其设置为分段函数:当y超出相位约束30°时，给一个很大的罚值1e6;当y在相位范围在30°以内时选择为目标函数的一个子元素，当y离开0越大时，则目标函数越大。总的目标函数为各个点目标函数的子元素代数和的绝对值。同时，我们把原来PSS参数的实测数据作为初值x0。

由发电机模型来确定传递函数的阶数，选取变量值的个数n。把图3所示传递函数的参数T1，T3…设为X1，X2…;把处在分母位置的T2，T4分别除以所对应的分子后T2/T1，T4/T3…将其设为Xn+1，Xn+2…;把Tw1=Tw2=T6设置为变量函数X2n+1。则约束条件为:

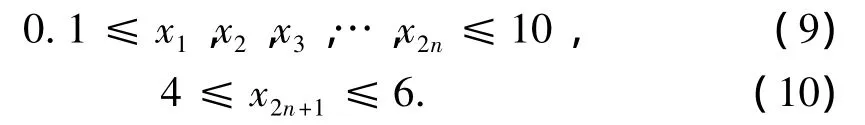
2.4 算法流程图

SQP算法流程图，见图4。

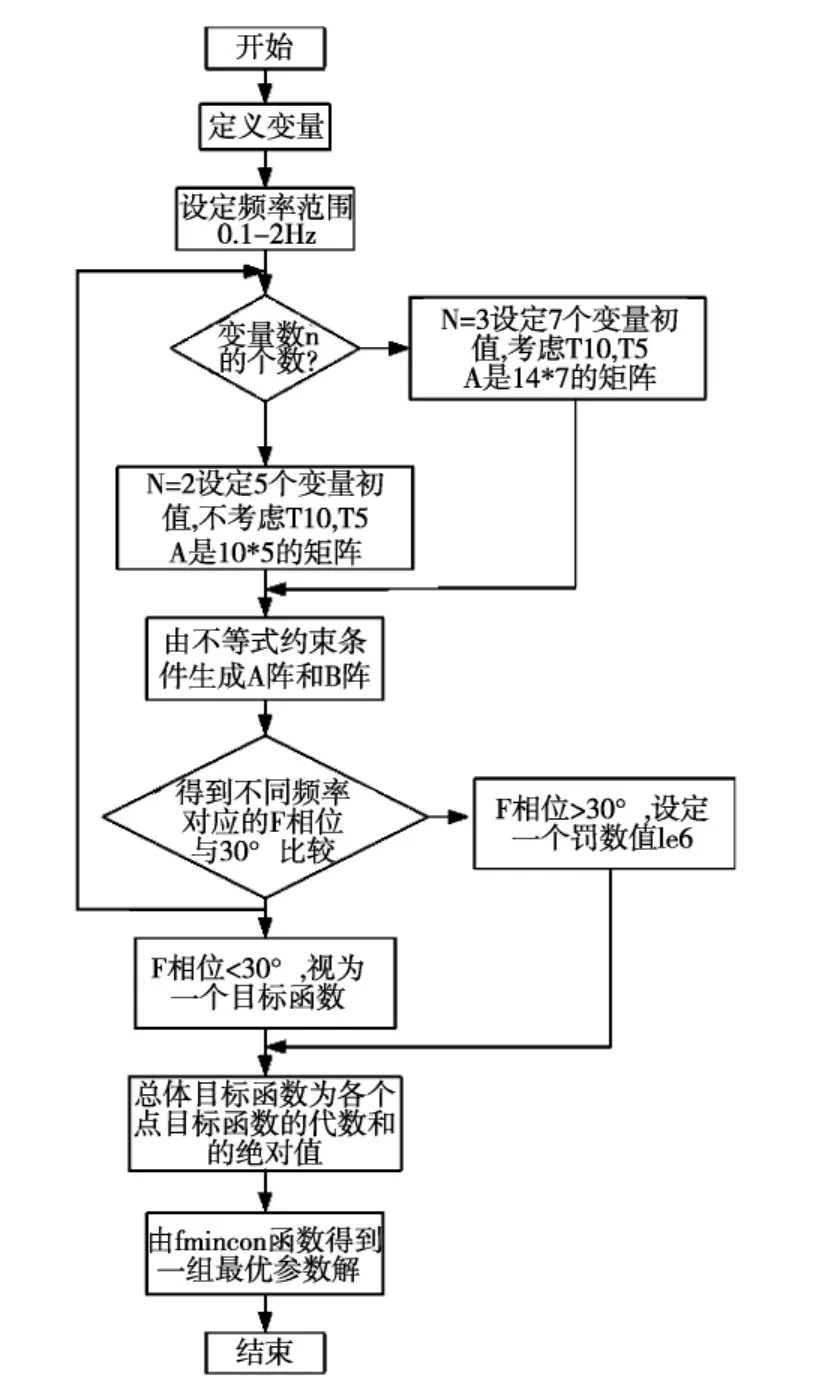
图4 算法流程图

3 算例分析

如图3所示为一个两机等值系统，其中G1是包含待可控PPS的600 MW机组，Gs为容量很大的等值机，代表等值主电网;G1通过双回500 kV联络线接到等值主网。两机等值系统在联络线回运行时，稳定性较好，但在一线因故障或检修退出后，容易出现低频功率振荡，需要投入并适当设定PSS参数，以解决低频振荡问题。

图5 两机等值系统

根据河北邢台电厂提供的数据，发电机的参数见表1。

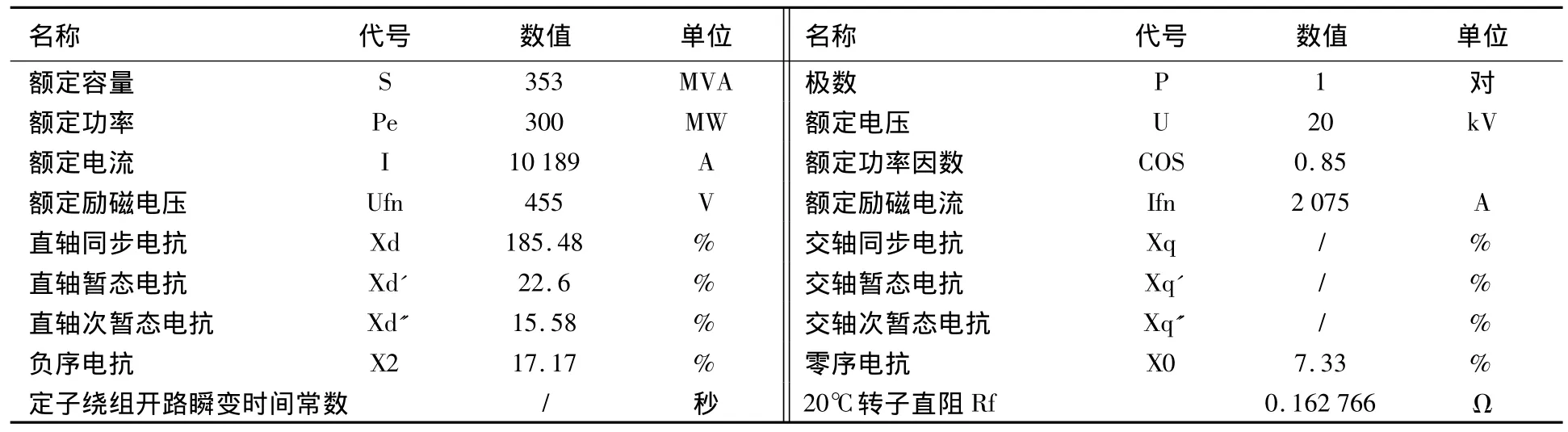
表1 发电机参数

为了验证SQP算法对PSS参数优化的有效性，任意设置50组初值，随机挑选进行参数优化，然后画出它们的bode图和目标函数相位图进行观察比较。

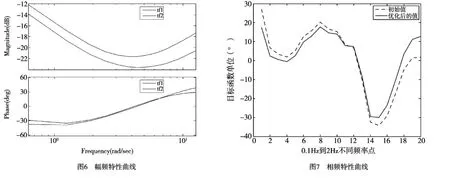
由图6我们可以得知tf1是由PSCAD仿真实验任一组参数画出的Bode图，tf2是通过程序参数优化后计算得到的一组参数画出的Bode图，通过对比两者幅频和相频特性，都基本吻合。说明经过Matlab参数优化后得到的PSS控制效果与通过仿真实验得到的PSS参数控制效果基本相同，验证了参数优化的有效性。

图7中虚线是由任意选定满足条件的一组初值得到的，可以看出有些点超出了-30°的范围，不能满足工程上的要求。而另一条实线则是通过参数优化后得到的，所有点取值都在±30°的范围内，可以得出经过参数优化后的相移特性使原来不符合工程要求的参数特性符合了要求，进一步说明了参数优化的有效性。

由优化程序解得PSS的一组参数为:T1=0.1165，T2=0.0016，T3=0.3788，T4=0.0064，T5=0，T6=0，Tw1=7.9264，Tw2=7.9264，T7=7.9264。通过PSCAD仿真实验验证参数的有效性，并对得到的△Pout波形进行 Prony［9，10］分析，如图 9 所示为参数优化前任意一组初值得到的△Pout和优化后△Pout对比。相应的主导振荡模态幅值和衰减率如表2所示。

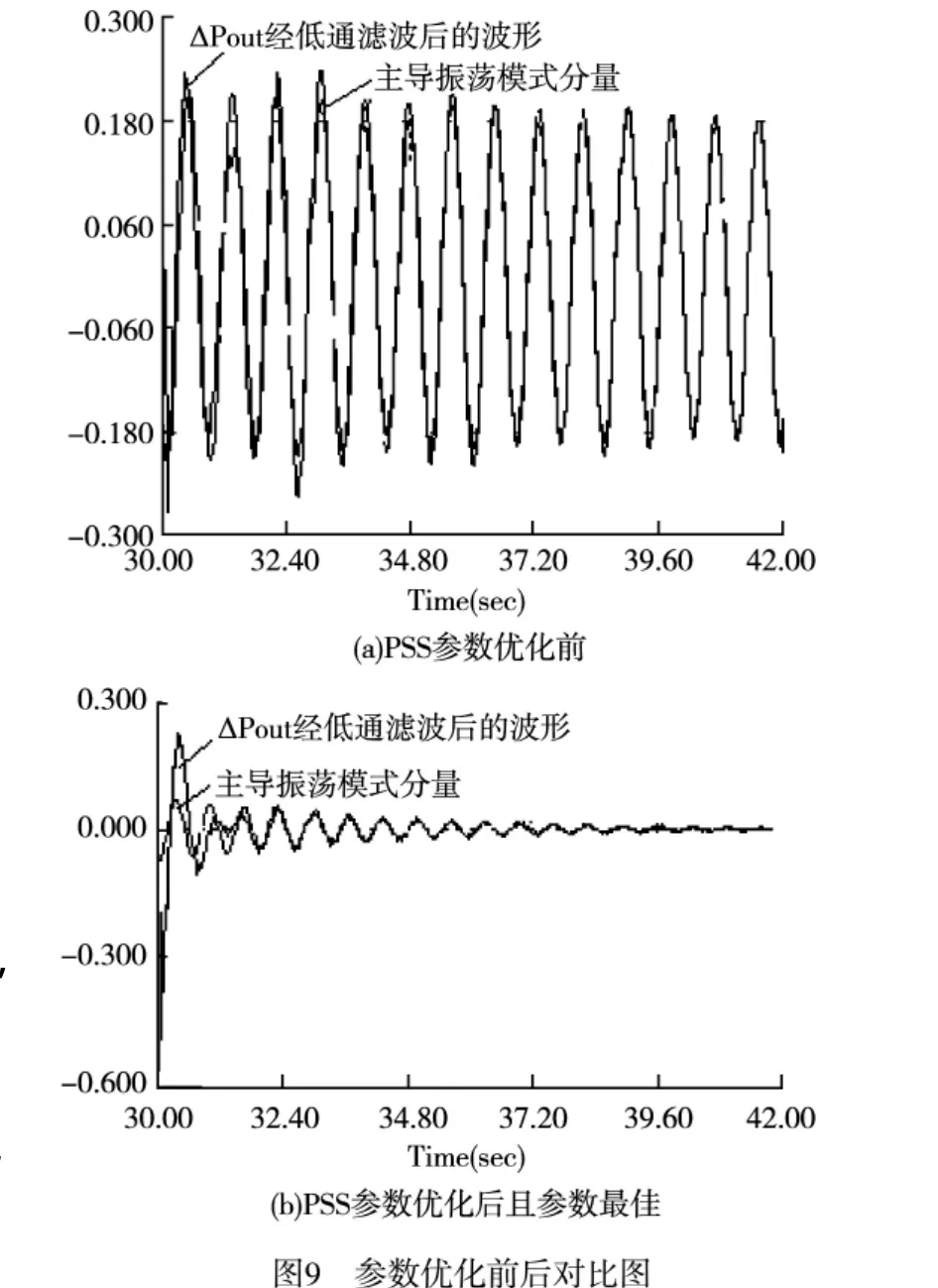
通过对比优化前后的图形和通过Prony分析得到的阻尼比，说明通过优化后的PSS使系统的阻尼得到增强，具有很好的鲁棒性，对低频振荡有更好的抑制作用，并且满足工程上的需要，具有一定的现场应用价值。

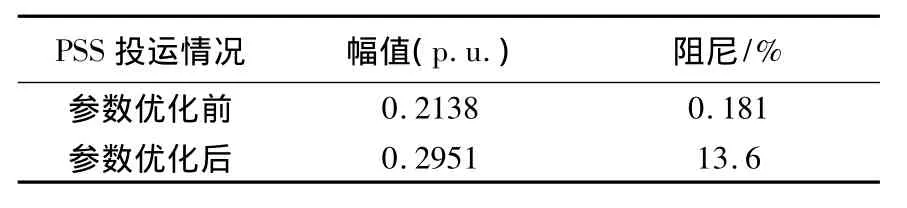
表2 Prony分析得到的主导振荡模态参数

4 结 论

本文根据河北邢台电厂的10号机组工程的实际需要设定了目标函数，使AVR+PSS与90°的相位差要在±30°之内，差值的绝对值越小越好。又考虑到PSS对抑制区域与区间振荡的不同频率，规定了它的频率取值范围在0.1 Hz到2.0 Hz之间，并设步长为0.1 Hz。根据PSS参数范围的要求设置了约束条件，建立了非线性不等式参数优化求解。得到一组最优解后通过PSCAD仿真实验进行验证，说明了PSS在参数恰当时可以有效的增大系统的阻尼，具有较好的鲁棒性，对低频振荡有很好的抑制效果。并且在初值不满足工程要求的条件下，通过参数优化可以得到一组满足条件的最优解。

［1］倪以信，陈寿孙，张宝霖.动态电力系统分析的理论和分析［M］.北京:清华大学出版社，2002.

［2］刘取.电力系统稳定性及发电机励磁控制［M］.北京:中国电力出版社，2007.

［3］Kundur P.Power System Stability and Control［M］.New York:McGraw-Hill，1994.

［4］方思力，朱方.电力系统稳定器的原理及应用［M］.北京:中国电力出版社，1996.

［5］Maslennikov V A，Ustinov S T.Method and Software for Coordinated Tuning of Power System Regulators［J］.IEEE Trans On Power Systems，1997，12(4):1419 -1424.

［6］Abdel-Magid Y L，Abdio M A.Simultaneous Stabilization of Multimachine Power Systems via Genetic Algorithms［J］.IEEE Trans on Power System，1999，14(4):1428 -1439.

［7］聂普焱，彭小飞.可行逐步二次规划法解非线性方程组［J］.高等学校计算数学学报.2004，26(2).

［8］王苏峰，王正志.基于遗传算法的逐步二次规划法的混合频域H_建模［J］.控制理论与应用，2001，18(2).

［9］卢晶晶，郭剑，田芳，吴中习.基于Prony法的电力系统振荡模型分析及PSS参数设计［J］.电网技术，2004，28(15).

［10］肖晋宇，谢小荣，韩英铎.电力系统低频振荡在线辨识的改进Prony算法［J］.清华大学学报，2004，44(7):883-887.