基于改进免疫算法的PMU多目标优化配置

张 健，李国庆，冀瑞芳

(1.吉林省电力有限公司调度通信中心，吉林长春130021;2.东北电力大学电气工程学院，吉林吉林132012)

相量测量单元PMU(Phasor Measurement Units)是基于全球定位系统GPS(Global Position System)的一种相量测量装置，它由微处理器、GPS接收器、信号变送模块及通讯模块组成，对电压电流进行同步测量［1，2］。PMU能够提供统一时空坐标下的高精度电压和电流相量量测，可显著改善电力系统量测可观测性和状态估计精度，提高系统监控的实时性和准确性。

现代电力系统规模很大，节点数众多，对大电网中所有节点都安装PMU是不现实的。如何用数量最少的PMU进行合理的安装配置以实现对全网各节点的完全可观测及量测冗余度最大化将具有很大的现实意义。本文以PMU安装数最少和量测冗余度最高为目标，建立了PMU的优化配置数学模型，并提出一种改进的免疫算法进行求解，得到PMU多目标优化配置方案的Pareto最优解集，最后用模糊集理论对最优解集中的解进行评价。

1 PMU最优配置

在电力系统中，电压相量可测或可求出的节点称为可观测节点，否则为不可观测节点。若系统的所有节点均为可观测节点，则系统为完全可观测系统;反之，系统为不完全可观测系统。

1.1 系统可观测性分析判定条件与方法

从网络节点方程可解性的角度，可给出如下节点可观测性的判定条件［3］:

1)配置PMU的节点及其相邻节点为可观测节点。

2)对于可观测的零注入节点，若其相邻节点中只有一个节点可观测性未知，其余都可观测，则可观测性未知节点为可观测节点。

3)对于可观测性未知的零注入节点，若其相邻节点皆为可观测结点，则该节点为可观测节点;若其相邻节点中包含可观测性未知的节点，其可观测性需要用节点方程理论来判断。

1.2 PMU多目标优化配置模型

若当所配置的全部PMU中任意一个出现故障时，均能保持可观测的节点，称之为冗余量测节点。对于一个N节点的系统，若采用某种PMU配置方案可存在R个冗余量测节点，则该方案的N-1量测冗余度定义为:D=R/N，PMU多目标优化配置模型为

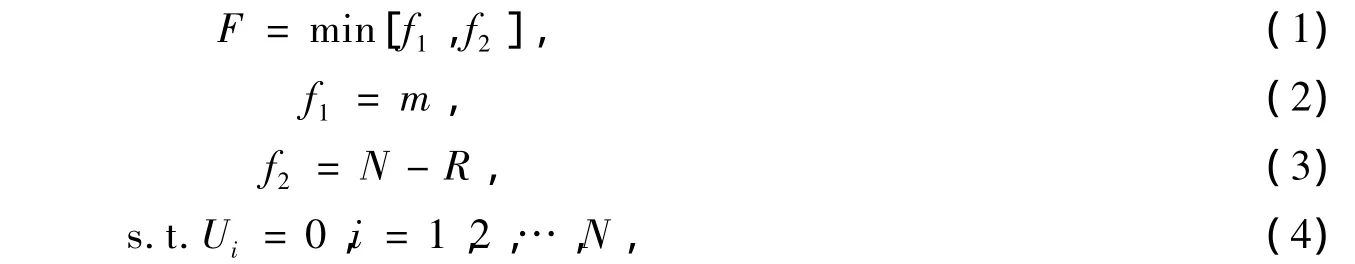
式中，m为PMU安装数量;Ui表示第i个节点不可观测;N为系统节点数。

2 多目标优化的免疫算法

多目标优化的免疫算法基于免疫应答原理，其主要思想是将求解问题的多目标函数对应入侵免疫系统的抗原，多目标函数的可行解对应免疫系统产生的抗体，用抗原和抗体亲和度来描述可行解和最优解的逼近程度。

2.1 多目标优化问题

多目标优化问题的目标函数Fopt可表示为:

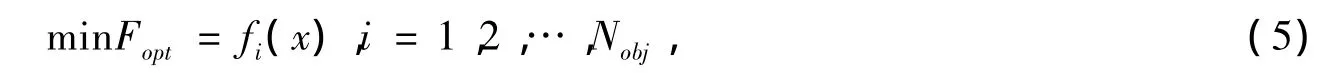
式中，fi(x)为第i个目标函数;Nobj为目标函数数量。

在进化算法中，个体都需要分配表示其优劣程度的适应度。在单目标问题中通过唯一的目标函数来实现，但在面对式(5)同时存在多个目标的情况时，评价个体的优劣变得相对复杂，适应度的分配问题成了难点。

2.2 Pareto 最优

Pareto可行解概念是建立在集合论基础上对多目标解的一种向量评估形式，在多目标优化问题中，常用到如下几个定义［4］:

定义1当且仅当满足 ∀i∈ {1，2，…，m}(fi(x1)≤fi(x2))，且 ∃j∈ {1，2，…，m}(fj(x1)＜fj(x2))时，可定义x1支配x2(表示成x1＜x2)。

定义2当x∈S且不存在x'∈S使得x'＜x，则可称x为集合S的非支配解，而包含所有这样非支配解x的集合P则称为S的非支配集。

定义3集合PF={vv=［f1(x)，f2(x)，…，fm(x)］T，x∈P}称为集合S的Pareto前沿。

2.3 改进免疫算法

免疫算法将求解问题的目标函数和约束条件作为入侵生物体的抗原，最优问题的可行解当作免疫系统产生的抗体。通过抗体和抗原的亲和度来描述可行解与最优解的逼近程度，通过一系列的进化操作及亲和度的计算，在保持抗体多样性的情况下，找到抗体种群中与抗原亲和度最大的抗体作为最优解［5］。

2.3.1 种群初始化

初始父种群Yi由随机产生的m个各不相同的长度为n的二进制编码(1代表该位置配置PMU，0代表不配置)个体组成，初始子种群Xi为空。

2.3.2 非一致性变异

传统免疫算法的变异算子的作用和变异代数没有直接关系，当算法进化到一定代数以后，由于缺乏局部搜索，很难通过该变异算子获得最优解。本文采用非一致性变异算子，该算子将变异结果与进化代数联系起来，使得在进化初期，变异算子的范围相对较大，而随着进化的推进，变异的范围越来越小，起到一种对演化系统的微调作用。具体操作如下:

设xk={v1，…，vs-1，vs，…，vl}是一个父抗体，抗体基因串长度为l，分量vk被选为进行变异，x'k={v1，…，vs-1，v's，…，vl}为变异后的抗体

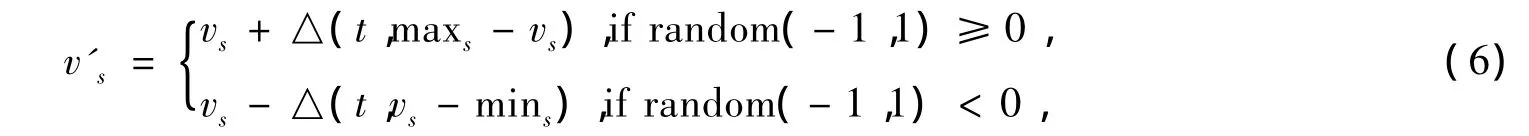
式中，maxs、mins为抗体基因vs取值的最大值和最小值;t为当前的进化代数，函数△(t，y)的值域为［0，y］，并使得当t增大时，△(t，y)接近于0的概率增加，即t的值越大，△(t，y)去接近于0的值的可能性越大，从而使算法在演化初始期能够搜索到较大范围，而后期主要是进行局部搜索。

函数△(t，y)的表达式为

式中r是［0，1］上的一个随机数;T表示最大代数;λ是决定非一致性程度的参数，起调整局部搜索区域的作用，一般取为2～5。

2.3.3 参数的自适应调整

当算法接近或陷入局部最优时，群体的多样性小，此时希望变异率大一些，使得个体在更广阔的空间扩展和突变，增加群体的多样性，以保证在局部搜索范围变大时局部搜索的有效性。在算法远离收敛状态时，群体的多样性大，此时希望变异率小一些，以保证群体的进化，使得在多个不同个体的领域内搜索。如果适当调节算法参数，既可保证群体的进化，又可提高算法的全局寻优性能。为此，引入参数的自适应调整策略，使得子种群在各自的进化过程中，变异率pm按亲和度自动调整。

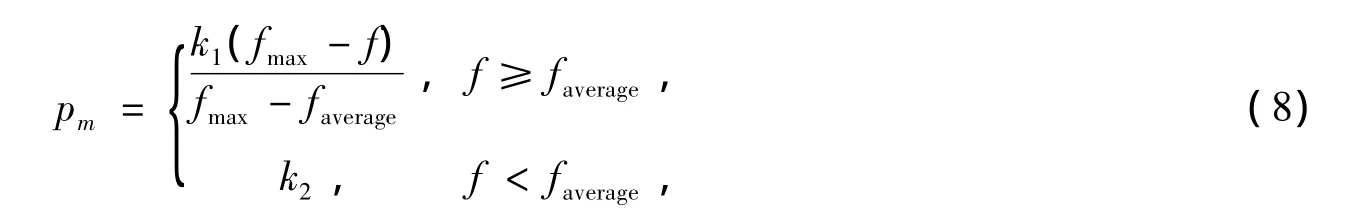
式中，f为待变异抗体的亲和度值;fmax为种群中抗体亲和度最大值;faverage为每代种群抗体亲和度的平均值;k1、k2在(0，1)内取值。

2.4 算法流程

PMU多目标优化配置的计算过程如下:

(1)为保持种群个体多样性，检验子种群Xg与父种群Yg中是否有重复的个体，若有则对该重复个体进行局部变异，直至两种群中的个体各不相同，并由式(6)计算所有新生个体的各目标函数值。将新的子种群Xg与父种群Yg混合成一个更大规模的临时种群Sg。

(2)按Pareto排序策略［6］，找出当前种群Sg的Pareto最优解集合，作为Yg(1)，将Yg(1)中所有个体从当前种群中移出，然后在剩余个体群中再找出新的Pareto最优解集合，作为Yg(2)，依此类推，直到所有个体都完成分级排序。然后，计算出各级中各个体的拥挤距离。

(3)将Yg(1)，Yg(2)，…按先后顺序形成一个新种群中，填充直到种群规模将超过m时，改为对Yg(i)中的个体按拥挤距离由大到小逐个补充，直到种群规模正好等于m时停止，形成新的父种群Yg+1。

(4)从Yg+1中按排序等级值越小越优先、同一等级则拥挤距离越大越优先的原则，采用随机锦标赛的形式产生优选种群，优选种群规模一般设置为父种群规模的一半左右。对以上优选种群采用2.3.1节中的非一致性变异机制，得到新的子种群Xg+1。

(5)若g=gmax，输出父种群即为多目标优化问题的Pareto最优解集;否则令g=g+1，进入下一次循环。

2.5 最优解评价

多目标优化得到的是一个Pareto最优解集，实际应用中决策者需要从中选择一个最优折衷解作为最终实施的方案，根据模糊集理论来确定最优折衷解［7］。每个Pareto解中各目标函数对应的满意度可用模糊隶属度函数来表示，定义如下

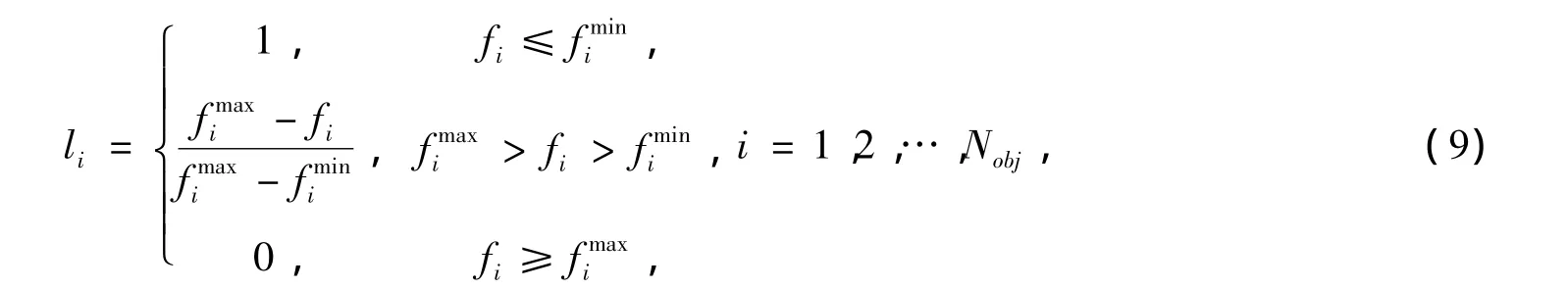
求得Pareto解集中各解的标准化满意度为

对Pareto最优解集进行评价，选择l值最大的为最优折衷解。

3 算例分析

本文采用IEEE-39节点系统［8］进行PMU多目标优化配置，取最大迭代次数为100，初始种群规模为100，k1、k2取0.5，λ取2.5，采用本文方法求解，得到能综合实现PMU安装数尽量少和冗余量测节点数尽量多两目标的一系列Pareto最优解，表1中列出了部分PMU多目标优化配置方案。

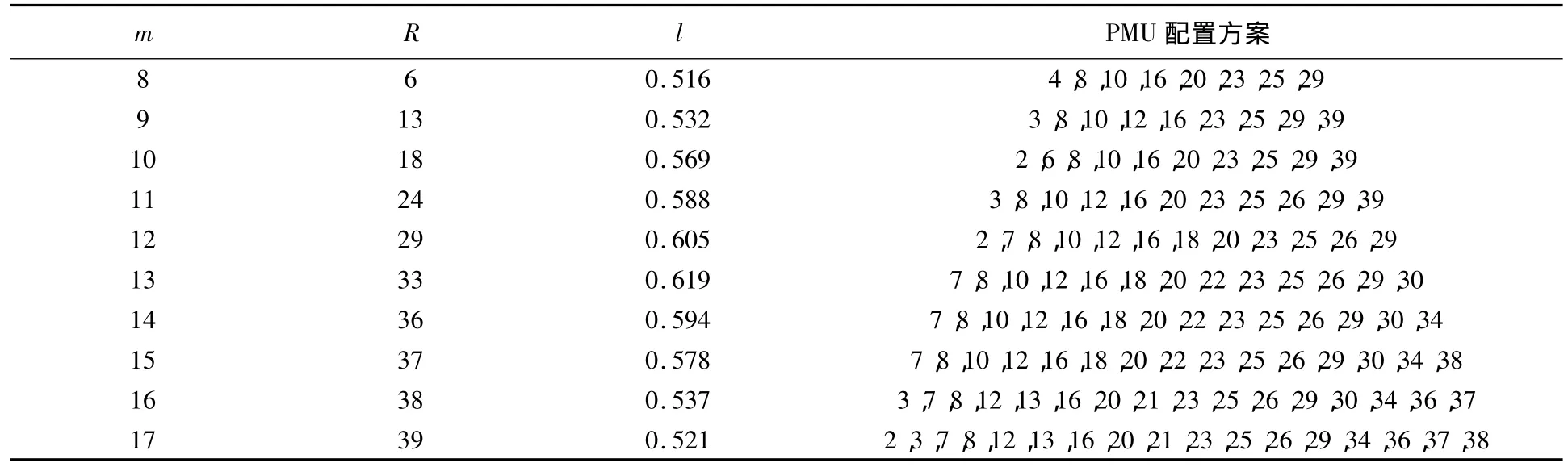
表1 PMU多目标优化配置方案

从表1中可看出，在全网完全可观测的前提下，要提高量测冗余度，则必须增加PMU，要实现全网完全可观测至少需要安装8个PMU，此时冗余量测节点数为6;若要完全实现全网N-1量测可靠性，即冗余量测节点达到100%，则至少需要安装17个PMU。各方案可通过标准化满意度来评估，当资金允许情况下，应选择满意度尽可能高的PMU配置方案，比较表1中各Pareto最优解的标准化满意度值，最优折衷方案可选择(7，8，10，12，16，18，20，22，23，25，26，29，30)。可见，本文的多目标优化方法可较大程度地改善PMU优化配置方案选择的合理性和灵活性，便于决策者根据实际情况需要选择最合适的配置方案。

4 结 论

本文将帕雷托分类排序与免疫算法相结合，对PMU进行多目标优化配置，目标函数选取为PMU的安装数目最小，且系统的N-1量测可靠性尽量高，采用模糊集理论提取出最优折中解，并通过非一致性变异操作来提高免疫算法的性能，改进后的免疫算法体现出优越的性能，可简单快速地实现全局多目标寻优，找到大量的Pareto最优解，得到准确而完整的Pareto前沿。得到的PMU多目标优化配置方案合理可行，对于相关决策者根据实际情况进行科学选择具有现实的指导意义。

［1］王克英，穆钢，陈学允.计及PMU的状态估计精度分析及配置研究［J］.中国电机工程学报，2001，21(8):29-33.

［2］蔡田田，艾芊.电力系统中PMU最优配置的研究［J］.电网技术，2006，30(13):32-37.

［3］杨明海，王成山.电力系统PMU优化配置方法综述［J］.电力系统及其自动化学报，2007，19(2):86-92.

［4］李智欢，段献忠.多目标进化算法求解无功优化问题的对比分析［J］.中国电机工程学报，2010，30(10):57-65.

［5］蒙文川，邱家驹.基于免疫算法的配电网重构［J］.中国电机工程学报，2006，26(17):25-29.

［6］彭春华，孙惠娟.基于非劣排序微分进化的多目标优化发电调度［J］.中国电机工程学报，2009，29(34):71-76.

［7］Farina M，Amato P.A fuzzy definition of“optimality”for many criteria optimization problems［J］.IEEE Trans on Power Systems，Man and Cybernetics，Part A，2004，34(3):315 -326.

［8］李强，于尔铿，吕世超等.一种改进的相量测量装置最优配置方法［J］.电网技术，2005，29(12):57-64.