考虑静态电压稳定约束的可用输电能力计算

运奕竹，李国庆，温佳鑫，张守龙

(1.东北电力大学电气工程学院，吉林吉林1320121;2.国电南京自动化股份有限公司，江苏南京211100)

电力市场环境下，由于经济性考虑、市场竞争、环境保护和土地使用等因素，使得电力网络的运行越来越接近其安全运行极限。如何准确确定系统潜在的功率交换能力来指导系统安全、经济运行，对电力市场各方参与者均具有重要的现实意义。电力系统可用输电能力(Available Transfer Capability)即ATC［1］，是指在现有的输电合同基础之上，实际物理输电网络中剩余的、可用于商业使用的传输容量。

现有的ATC研究方法可以分为:基于概率的研究框架和基于确定性分析方法的研究框架［2］。概率性研究方法可计及系统各种不定因素对ATC的影响，适用于系统规划。确定性研究方法能计算出确定系统状态和安全约束下的ATC，也是概率性研究法中单一样本的求解方法。

从数学的角度解读ATC的定义，确定性研究方法可以将ATC看作是一个计及系统安全约束的优化问题。故ATC的确定性研究方法主要有直流潮流法［3］、连续潮流法(Continuation Power Flow，CPF)［4］、最优潮流法(Optimal Power Flow，OPF)［5］，以及辅助性的灵敏度分析法［6］。其中，能够方便、有效地考虑系统静态安全约束的方法为OPF法和CPF法。OPF方法是将所研究问题转化为求解满足各种约束的系统最大负载能力，其最大的优点是可以全面考虑各种约束条件并通过优化技术获得待研究设备的最佳状态;不足之处是OPF法所获得的结果是一个理想的目标方案，最优解可能是系统从当前状态无法过渡到的一个最优点［7］。CPF法通过在常规潮流方程中添加连续型参数，克服了常规潮流计算方法在系统运行点接近鞍结分岔点时发散的问题，能得到准确的P-V曲线，有较强的鲁棒性;但CPF方法计算中，发电机出力的增长方向是确定方向，与实际系统运行情况并不符，计算结果趋于保守从而限制了输电系统的利用率［7］。

基于以上所述OPF法和CPF法的特点，本文首先构建电力系统区域间ATC求解的VSC-OPF模型，该模型不仅能考虑常规静态安全性约束而且能够计及静态电压稳定性约束，该模型将连续型方法与OPF模型相结合，研究负荷增长因子变化对系统区域间ATC值的影响;然后，借助于内点法对优化模型进行求解得到最优解，随着负荷增长因子的由小到大的变化能够得出一个由最优点构成的解轨迹，根据解轨迹上所取的系统运行点到电压崩溃点的距离，可得到不同电压稳定裕度所对应的ATC值;所建模型将OPF法与CPF法的优势相结合，可全面考虑各种约束条件，并确保所求最优解是系统从当前状态能够过渡到的一个最优点。最后，以IEEE-30节点3区系统的仿真分析验证了所建模型和方法的合理性和有效性。

1 ATC求解模型

本文中，ATC计算采用的目标函数是送电区域对外联络线的总传输功率与基态潮流之差的最大化［8］，即

式中，Pi、Qi分别为节点i注入的有功和无功功率;Vi、Vj分别为节点i、j的电压幅值;θij为节点i、j间的电压相位差;Gij、Bij为节点i、j间的支路电导和电纳。

不等式约束为交流系统发电机组出力约束、负荷容量约束、无功补偿容量约束、节点电压和支路电流约束，即:

式中，αG为所有发电机节点集合;αL为所有负荷节点集合;αN为系统所有节点集合;min、max分别表示变量的下限和上限。

2 VSC-OPF模型

电力系统的VSC-OPF模型［9］是一种考虑了电压稳定性约束的最优潮流模型，该模型将连续型方法与最优潮流模型相结合，研究参数变化对系统最优性的影响，可得出一条由最优点构成的解轨迹，VSC-OPF模型的具体形式为:

式中，f(p，λ)为VSC-OPF的目标函数;h(x，p)为系统基态潮流方程约束;^h(x，p，λ)为连续潮流法的潮流方程约束;g(x)和g(^x)分别为基态和连续潮流下的交流系统发电机组出力约束、负荷容量约束、无功补偿容量约束、节点电压和支路电流约束;p为系统控制变量;min、max分别表示变量的下限和上限值;λ为负荷增长因子，随着λ按规定方向变化，发电机和负荷的有功功率可表示为:

VSC-OPF与OPF本质都是求解优化问题，因此求解方法相同，只是VSC-OPF在每次迭代过程中需计算CPF并进行变量的校验，最终使目标函数达到全局最优。

3 CPF法

连续型方法是用一种跟踪非线性动态系统平衡点解轨迹的基本方法［10］，连续型方法常用的是带预测—校正的连续型方法，该方法由预测、校正、参数化及步长控制4个部分组成。连续型方法与电力系统静态潮流相结合构成了电力系统常用的连续潮流法(CPF)，其基本求解原理如图1所示，CPF的整体求解过程如下所述:

参数化的CPF潮流方程可表示为:

式中，x为节点电压幅值和相位的集合;λ为负荷增长因子。参数化的负荷方程和发电机出力方程如下:

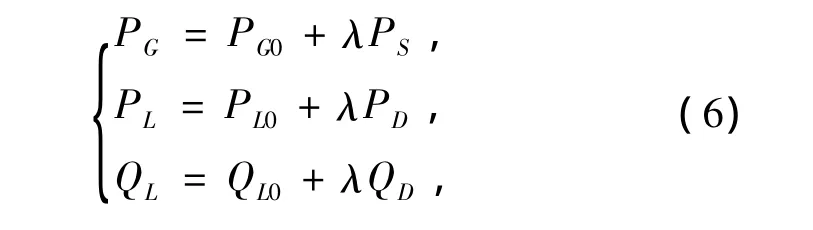
图1 连续潮流法原理

式中，PG0、PL0、QL0分别为系统基态时的发电机的有功功率和负荷的有、无功功率;PS、PD、QD为发电机和负荷的功率增长方向;

(1)预测环节，预测环节是根据当前点p处的解以及p点以前几个点的解给出解轨迹上下一个点q的估计值，估计值的好坏直接影响校正环节中准确解的迭代次数，预测的结果将直接影响整个连续型方法的计算效。在连续潮流法中，预测环节常用的方法是切线法，该方法可描述为:由点p是式(5)的一个平衡点，则满足:g(xp，λp)=0，则式(5)对负荷增长因子λ在p点的导数可表示为:

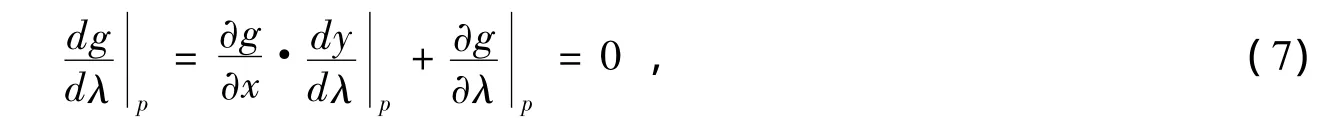
对应的p点的切向量可近似表示为:

由式(7)和式(8)可得:

引入步长控制系数k，以确定点p处负荷增长因子λ的增加量△λp，△λp及△gp可表示为:

式中，步长控制系数k取值为±1，正号表示负荷增加;负号表示负荷较少。

由式(10)，可求出c点负荷增长因子的估计值^λc及节点电压幅值和相位的估计值^xc为

(2)校正环节，校正环节就是以^λc和^xc为初始点计算、校正准确得出满足潮流方程的λq和xq，即求解如下所示的扩展非线性方程组:

其中，ρ(x，λ)满足正交参数化，即

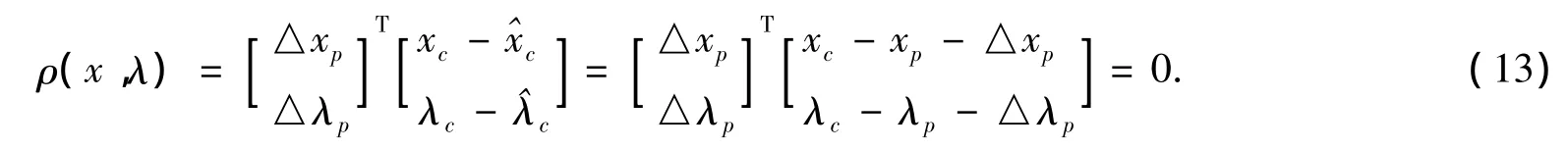
通过上述过程，整个系统平衡解轨迹即可准确追踪。

4 内点法(IPM)求解过程

本文针对基于VSC-OPF的ATC计算拟采用内点法［11］进行求解。自Karmarkar在1984年提出一种具有多项式时间可解性的线性规划内点算法以来，多种类型的内点算法相继被提出。其中路径跟踪法，即非线性原对偶内点法最具发展潜力。它本质上是拉格朗日函数、对数壁垒函数和牛顿法三者的结合，具有二阶收敛性和数值鲁棒性。在保持解的原始可行性和对偶可行性的同时，沿原 -对偶路径迭代直至寻找到目标函数的最优解。很好地保留了牛顿法的优点，同时较牛顿法更方便地处理了各种函数和变量不等式约束。内点法求解系统优化问题的具体过程为:

对非线性规划问题:

式中，f(x)为目标函数;h(x)为等式约束;g(x)为不等式约束;gmin、gmax为不等式约束的上、下限。(1)引入松弛变量l、u，把不等式约束转换为等式约束:

式中，l＞0，u＞0。

(2)将原问题转化为优化问题，针对优化问题形成的拉格朗日函数为:

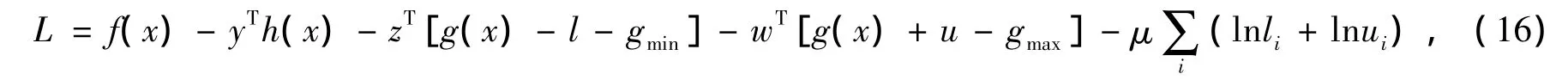
式中，y、z、w均为拉格朗日乘子。

(3)根据内点求解的KKT条件有:

式中，▽表示对x求偏导，即求雅克比矩阵;e是单位向量。

(4)采用牛顿法对式(16)所示的非线性方程求解，对应的修正方程:

(5)求解式(18)，对于第k次的迭代的修正量。第k次的近似解为:

式中，αp、αd的步长为:

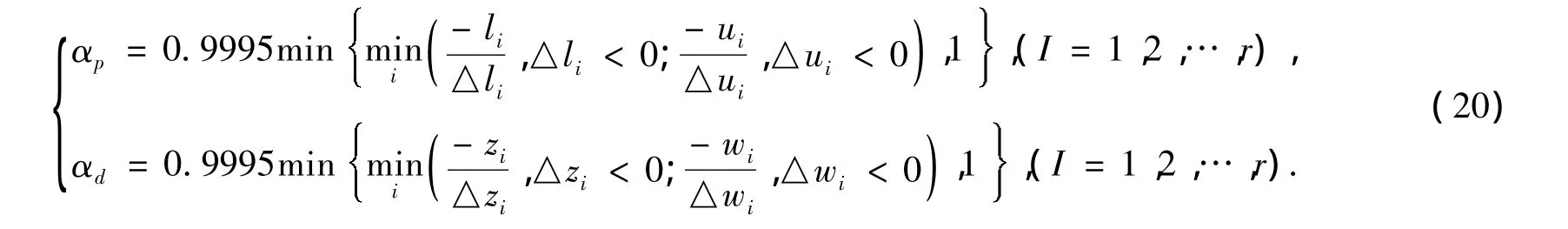
(6)计算第k次迭代的对偶间隙:

判断Gap≤ε，若满足输出ATC计算结果，程序中止;若不满足，程序回到(3)，直到k＞kmax，输出迭代失败，中止程序。

5 算例分析

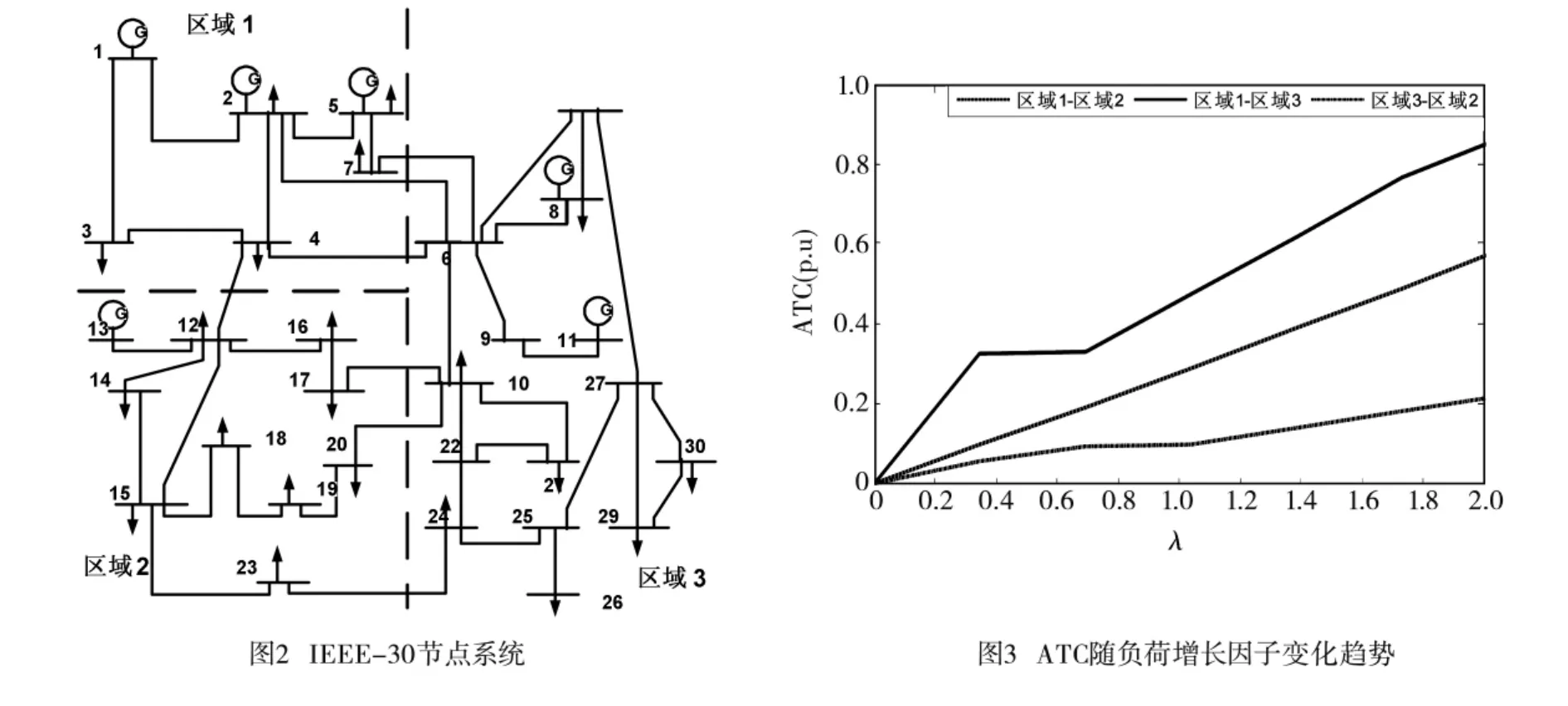
为验证所建模型及算法的正确性和有效性，本文采用IEEE-30节点系统进行计算分析，系统参数详见文献［12］。整个系统划分为三个区域，详细分区情况如图2所示。

系统基态下和基于VSC-OPF模型计算得到的1-2区、1-3区和3-2区各区域间联络线上流过的功率和系统区域间ATC值如表1所示。

表1 VSC-OPF计算结果

采用VSC-OPF求解系统区域间ATC时各节点注入的有功功率见表2，限于篇幅，本文中表2中仅列出了区域1-3在λ=2.0724、ATC=0.87102时各节点注入的有功功率。

表2 各节点注入有功功率

IEEE-30系统随着负荷增长因子由小到大的变化所得到系统区域间ATC值见表3，最优点解轨迹见图3。根据表3，可以看出在能够满足系统静态电压稳定要求的前提下，负荷增长因子最大为λ=2.0724。由图3，可以看出系统随着负荷增长因子的增长，即系统运行距离电压崩溃点的距离越近，ATC值是不断增大的。最优解轨迹表明，所得最优点均是系统从当前状态能够过渡到的最优点。

表3 负荷增长因子变化对各区域间ATC值影响

6 结 论

本文首先构建电力系统区域间ATC求解的VSC-OPF模型，该模型不仅能考虑常规静态安全性约束而且能够计及静态电压稳定性约束，该模型将连续型方法与OPF模型相结合，研究负荷增长因子变化对系统区域间ATC值的影响;然后，借助于内点法对优化模型进行求解得到最优解，随着负荷增长因子的由小到大的变化能够得出一个由最优点构成的解轨迹，根据解轨迹上所取的系统运行点到电压崩溃点的距离，可得到不同电压稳定裕度所对应的ATC值;所建模型将OPF法与CPF法的优势相结合，可全面考虑各种约束条件，并确保所求最优解是系统从当前状态能够过渡到的另一个最优点。最后，以IEEE-30节点3区系统的仿真分析验证了所建模型和方法的合理性和有效性。

［1］North American Electric Reliability Council(NERC).Available transfer capability definitions and determination［R］.1996.

［2］李国庆，王成山，余贻鑫.大型互联电力系统区域间功率交换能力研究综述［J］.中国电机工程学报，2001，21(4):20-25.

［3］Landgren G L，Terhune H L，Angel R K.Transmission interchange capability analysis by computer［J］.IEEE Trans.on Power Apparatus and Systems，1992，91(6):748 -754.

［4］王成山，李国庆，余贻鑫，等.电力系统区域间功率交换能力的研究(一):连续型方法的基本理论及应用［J］.电力系统自动化，1999，23(3):23 -26.

［5］李国庆，沈杰，申艳杰.考虑暂态稳定约束的可用功率交换能力计算的研究［J］.电网技术，2004，28(15):67-71.

［6］程超，李华强.可利用传输能力的快速计算［J］.电网技术，2009，33(3):49-52.

［7］王成山，李慧聪，魏炜，等.考虑电压稳定性约束的输电能力综合计算［J］.电力自动化设备，2004，24(1):9-13.

［8］汪峰，白小民.基于最优潮流方法的传输容量计算研究［J］.中国电机工程学报，2002，22(11):35-40.

［9］Rao K N，Amarnath J，Kumar K A.Voltage constrained available transfer capability enhancement with FACTS devices［J］.ARPN Journal of Engineering and Applied Sciences，2007，2(6):1 -9.

［10］李国庆.基于连续型方法的大型互联电力系统区域间输电能力的研究［D］.天津:天津大学，1998.

［11］李国庆，姚少伟，陈厚合.基于内点法的交直流混合系统可用输电能力计算［J］.电力系统自动化，2009，33(3):35-39.

［12］李国庆，陈厚合.改进粒子群优化算法的概率可用输电能力研究［J］.中国电机工程学报，2006，26(24):18-23.