基于细菌群体趋药性算法的可用输电能力计算

陈厚合，廖海亮，李国庆

(东北电力大学电气工程学院，吉林吉林132012)

可用输电能力(Available Transfer capability)ATC是指在现有的输电合同基础上，实际物理输电网络中剩余的、可用于商业使用的输电容量［1］。在市场环境下，不能精确、可靠地反映网络实际的ATC水平，都会导致市场参与者的利润、系统运行安全可靠性以及用户服务水平的严重降低。因此，作为衡量电网安全稳定运行的重要指标及引导资源优化配置的ATC，已成为电力系统急待解决的热点问题之一。

近些年来，各国学者对系统ATC计算展开了大量研究，并取得了一定的成果。目前，常用计算ATC的方法有:1)线性分布因子法［3］，该方法以直流潮流为基础，忽略了电压和无功功率地影响，因此计算量小，求解速度快，但该法的快速以牺牲一定准确度为代价，且在缺乏无功功率支持和有效电压控制的重负荷系统中会出现无法接受的误差;2)连续潮流法［4］，该方法考虑了系统非线性和电压无功特性，具有较强实用价值，不过由于该法在计算中未进行发电机和负荷功率的优化，计算结果偏保守;3)最优潮流法，该方法综合考虑包括潮流方程、输电线路容量极限和电压限值等系统约束，将ATC问题转化为最优化问题，求出理论最优解，对于这类最优化问题，可利用多种优化算法求解，如:内点法［5］、连续二次规划法［6］和 Benders［7］算法等传统经典算法，以及遗传算法［8］、改进粒子群算法［9］等人工智能算法。

然而，经典优化算法要求ATC目标函数连续可微且采用单一搜索机制，很难跳出局部最优;智能算法需给出诸如罚函数、交叉率、变异率、初始染色体群等参数，而这些参数选取至今仍无确定的准则。细菌趋药性算法［11］(Bacter Colony，简称BC)是一种从细菌行为中获得灵感的优化方法。2005年，我国学者李威武等人在此基础上提出细菌群体趋药性算法［12］(Bacter Colony Chemotaxis，简称BCC)。该算法中，细菌不仅继承了BC算法中使用自己的运动位置信息进行函数优化，同时也利用其他细菌的位置信息进行函数优化。BCC算法自身的寻优特点使其在一些问题上的优化速度和精度上优于其他一些常见的优化算法［2］，该法在电力系统无功优化上取得较为理想的结果［13，14］。

综上所述，本文构建基于最优潮流模型的ATC计算模型，并借助BCC算法求解该模型。针对售电区发电机及送电区负荷的n维变量寻优问题，提出将该n维空间的寻优问题化简为(n-1)个二维空间求解，并给出对应的求解表达式;针对ATC求解的特点，引入自适应步长和公告板，提高了ATC求解运算速度，同时保证ATC求解过程中的全局搜索能力。最后通过IEEE-30节点系统对该方法进行了仿真验证。

1 BCC算法简介

1.1 单个细菌移动描述

细菌在营养剂或引诱剂环境下，会进行相应的反映活动。收集信息，进行移动，在移动中不断修正方向和步长，找到环境中最有营养的位置。细菌对营养剂或引诱剂的反映运动遵守参考文献［11］的假设。假设细菌群体所处的环境是一个n维空间，则细菌移动步骤如下:

步骤1系统参数设定，在整个算法中，当期望的精度ε给定后，可以得到如式(1)～(3)所示的T0，τc，b三个系统参数。

式(1)～(3)是由细菌运动轨迹方程线性回归统计得出的，T0是最短平均时间，与计算精度有关的参数，τc是与细菌运动方向转角相关的时间，b是与维数无关的参数。

步骤2选择移动方向，当细菌个体移动时，用移动步长和移动方向即一个半径r和(n-1)个角度(φ1，φ2，…，φn)表示细菌在n个维度中相邻维度两两组合所构成的平面内的移动角度，即把细菌的n维移动转化成(n-1)个二维移动，这(n-1)个移动角度综合叠加结果就是细菌完成在整个n维空间中的移动方向选择。

设i(i=1，2，…，n)为维度编号，细菌移动新方向的确定是用角度φi在(i，i+1)二维空间内的高斯概率密度分布确定的，其中φi从i轴侧量向左或向右取角度值，分别服从如下概率分布:

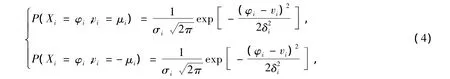
φi的取值范围为［0°，180°］，向左或向右的确定按下式(5)所示的统一的概率密度分布:

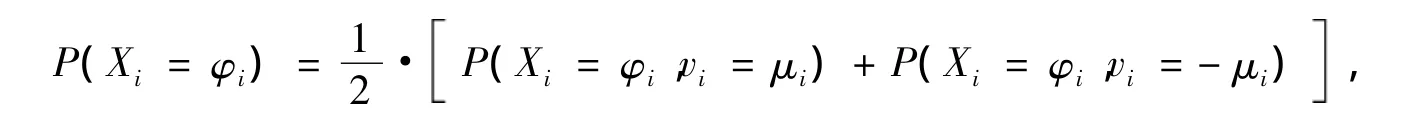
期望μ=E(X)和方差σ=Var(X)分别按满足如下公式:fpr为当前点和上一个点的函数值的差;lpr为变量空间中连接当前点和上一个点的向量模;其中τc为相关时间，τpr为细菌上一运动轨迹的持续时间。它不是直接作为决定移动效果的控制量，而是作为一个关系到移动方向的调整参数，即上一步中的参数τ，τ由式(10)所示的概率分布决定:

参数T由下式决定:

其中，T0为最小平均移动时间;b为与维数无关的参数。

一旦φi确定后，可以得到一个新的单位矢量nu，为了获得这个矢量，我们把新确定的角(φ1，φ2，…，φn-1)与以前的移动角求和。

步骤3移动步长的确定，在n维空间中定义一个位置坐标(X1，X2，…，Xn)，则这个坐标向量可以唯一描述一个细菌的空间中的位置。我们定义细菌在n维空间中移动步长为(x1，x2，…，xn)。针对文献［9］中由于n维空间细菌移动随着维数增加步长变小，不利于收敛，本文把n维空间的细菌移动方式转化成(n-1)个二维移动，这(n-1)个移动结果完成了细菌在n维空间的一次移动，具体表达式如下:

在整个优化过程中，细菌仅利用它上一步或上几步的位置信息来近似模拟未知的梯度信息，一般认为这是一种随机梯度近似的搜索方法［15］，即利用相邻一步或几步的位置信息来模拟未知的梯度。由于新的移动方向和持续时间都是按概率决定的，BC算法暗含了细菌有一定的摆脱局部最优到达全局最优的能力。然而，单个细菌必须在解空间中探索许多不同的点来模拟和修正它形成的梯度信息，因此该算法本身在寻优速度上慢于群体优化算法。

1.2 引诱剂环境下细菌信息交互模式

在自然界中，细菌以群体的形式存在，细菌之间通过各种方式交换食物信息。使用同伴提供的信息，细菌能大大扩展对于环境的了解从而能增加存活的几率。假定细菌个体间进行联系的方式如下:

(1)每个细菌有一定的感知范围，本文假定每个细菌都有全局的感知范围;

(2)每个细菌都可根据它感知范围内其他细菌的信息来调整移动方式。

根据上述两个假设条件，细菌在群体环境中移动行为可描述为:

(1)每次移动到新位置前，细菌要感知它周围的环境，试探旁边是否有其他更好的细菌。如果有，那么它有可能趋向移动到这些拥有较好位置细菌的中心点。在移动步数为k时，细菌i附近有更好位置同伴的中心点由下式决定:

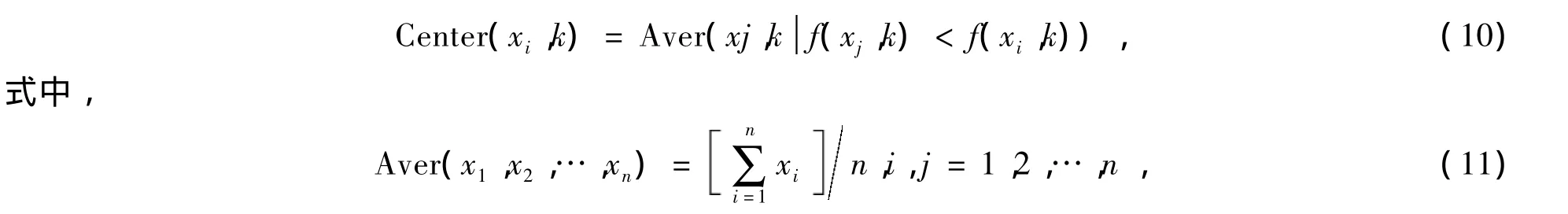
(2)如果一个细菌趋向移动到它周围同伴的中心位置，那么移动步长为 rand()·dis(xi，k，Center(xi，k))，rand()为(0，2)之间服从均匀分布的随机值。

(3)改进策略，菌群每移动一步后，位置最差的细菌继续移动到菌群整体移动前位置最好的细菌所处的位置附近，即:

利用单个细菌移动轨迹的信息和感知到的周围同伴的位置信息，BCC算法具有BC算法易跳出局部最优的优点，也拥有群体算法的强大空间搜索能力，从而能够更快找到全局最优点。

2 基于BCC算法的ATC的数学模型

2.1 ATC数学模型

ATC计算的优化模型包括目标函数、等式约束条件和不等式约束条件。在忽略网络损耗的前提下，常用的计算ATC的目标函数有6种［16］，为了与经典算法中的Benders算法［7］的结果做比较，本文选择相同的目标函数:

等式约束:

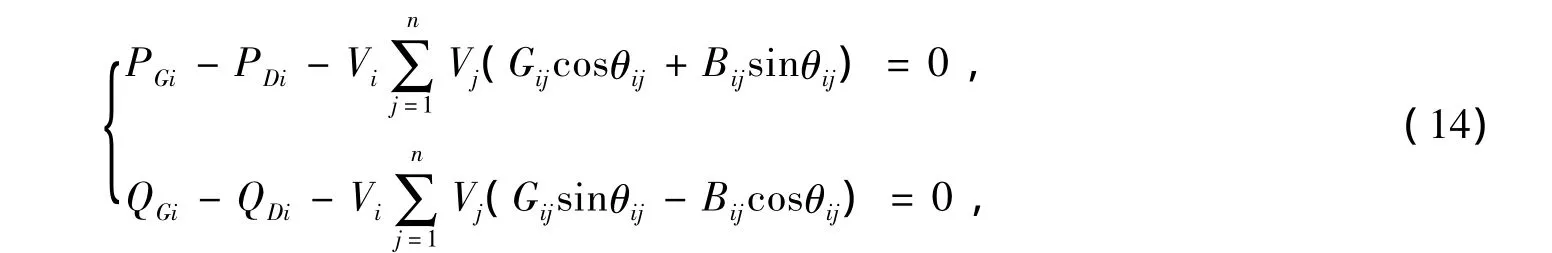
式中:△PDi表示节点i的负荷有功的增量;PGi，QGi分别为发电机i的有功和无功功率;PDi，QDi分别为节点i上的负荷有功和无功功率;n为节点总数;Vi，θi分别为节点i的电压幅值和相角;θij=θi-θj;Gij+jBij为系统节点导纳矩阵Y中相应的元素。

本文的不等式约束参考静态安全约束中元件正常运行时的约束［17］，限于篇幅，未考虑N-1法则，考虑N-1法则的ATC问题详见［7］:

发电机组出力约束:

节点电压约束:

线路容量约束:

交易约束:

式中:Sn为所有节点的集合;SG为送电区域所有发电节点的集合;SD为受电区域所有负荷节点的集合;变量上角标中的*、min、max分别表示基态潮流中的标幺值、变量的下限和上限。

2.2 算法实现及流程

结合BCC算法，设细菌个数为n，细菌坐标变量的维数是由发电区域发电机个数(记为G)除去一台当作平衡机组外其余发电机的有功(共(G-1)个变量)、受电区域负荷节点个数(记为L)的有功和无功(共2L个变量)组成，构成一个n·(2L+G-1)阶初始矩阵，并在基态潮流基础上随机初始化矩阵元素。这些控制变量在算法中表征细菌移动寻优时的空间位置。根据实际问题需要，以发电机出力上下限、负荷处功率上下限为约束条件，细菌每移动一步后对移动结果进行比较，并进行相应调整，避免坏数据产生。

(1)约束的处理

ATC问题的约束条件包括等式约束条件和不等式约束条件。由于潮流计算本身已满足等式约束，因而降低问题的复杂程度;本文采用罚函数法［18］处理不等式约束，根据不等式约束在计算过程中越界量的大小，动态地调整其罚函数而不是固定罚因子为常数。将ATC问题的求解转化为无约束优化问题进行求解。

对于原优化问题的抽象数学模型:

首先，将不等式约束的越界量以惩罚项的形式附加在原来的目标函数f(x，u)上，构造出细菌群算法的适应度函数(即惩罚函数)F(x，u):

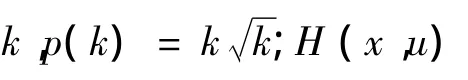
式中，t=max{0，hi(x，u)};θ(t)为惩罚系数;γ(t)为惩罚力度。

由上式可知，惩罚系数θ(t)与惩罚力度γ(t)的值随着不等式约束条件的越界函数hi(x，u)的量的大小而动态调整。在本文中，罚函数的参数选择如下:

(2)公告板

公告板用以记录各代细菌群体的位置状态xibest，k+1和这些位置的引诱剂浓度fbest(xi，k+1)。各细菌从此处判断自己的位置是否最好，如果超过以往最好记录，将最好记录进行刷新［19］。通过公告板的应用，可以将每个细菌移动的最优位置保留下来，防止移动过程中细菌最优位置的丢失，从而提高计算速度。

(3)自适应调整误差εb

由公式(1)～(3)知ε对参数设定影响很大，并因此影响细菌每次移动寻优步长及方向。因此如何设定εb对于函数优化十分重要。本文采用自适应调整εb的方法:即在函数优化刚开始时，εb选择一个较大的初值，此时细菌移动步长就比较大，这样可以使细菌以较大步长寻优，避免在局部范围过多的耗费时间;当经过若干次移动之后，如果Vf连续ninter代的值小于某个预设的误差值(取1，0.1等)时，说明此时的细菌位置已经靠近最优位置，因此εb应通过以下公式进行更新:

其中，α为大于1的正数。具体取值如下:

当 εb＜ε 时，取 εb= ε。

自适应调整参数εb能够根据Vf大小灵活的调整步长及寻优方向，爬坡速度快，缩短寻优时间，具有良好的全局寻优和局部细搜索的能力，有较强的克服局部寻优的能力。BCC算法求解ATC的程序框图，见图1。

3 算例分析

图1 BCC算法求解ATC的程序框图

3.1 算例描述

本文以IEEE-30节点系统为例验证所建立ATC模型及BCC算法的有效性和可行性，并与传统Benders算法进行比较。该系统共有6台发电机，41条线路，该系统划分为3个区，具体分区情况如图2所示，系统详细参数见文献［7］。BCC算法参数设定:细菌群规模N=20;初始精度εb=10;最终精度ε=0.01;移动半径r=1;基准功率SB=100 MVA。

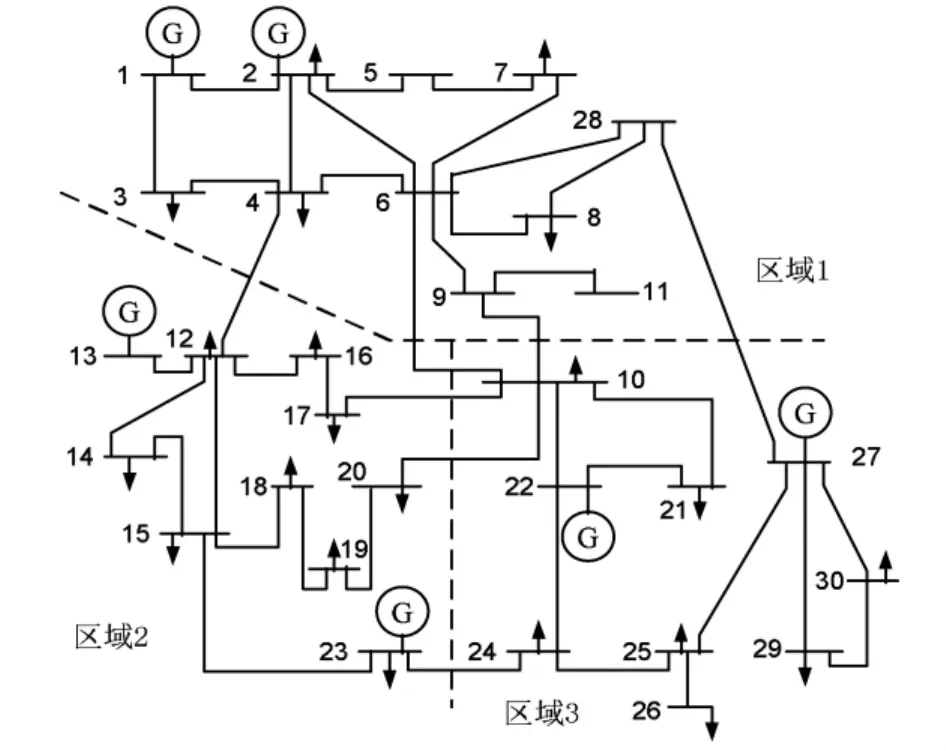
图2 IEEE-30节点系统

3.2 结果分析

表1为采用Benders算法、IPSO、BCC的计算ATC值。从表中可以看出，BCC算法得到的最优解均优于传统算法得到的最优解。其中，BCC算法得到的ATC在区域2-1、3-1和3-2区的最优解远大于benders算法的结果。这是因为传统算法采用单一搜索机制，因此容易陷入局部最优解。而BCC算法每个细菌能够在n维空间的各方向搜索，并且移动步长和移动时间具有多样性，使得菌群容易跳出局部最优解而趋向全局最优解。通过BCC算法与IPSO算法结果相比较可以看出，除了1-3区，BCC算法得出的ATC值比IPSO更大些，这是因为BCC算法在接近最优值时随机调整了寻优步长及时间，这样搜索的结果更容易接近最优解，同时也验证了文献［12］所说的在某些算例上优于一些常见的优化算法的结论。

表1 IGA与Benders、IPSO算法计算结果比较

表2 2-3区ATC各控制变量值

为进一步验证BCC算法如何求解ATC，本文以2-3区BCC计算结果为例，说明如何调整送电区发电机功率的输送以及受电区节点负荷功率的增量，使两区域ATC达到最大。2区有两台发电机，假设其他区域发电机按基态潮流发电，在运算中以2区其中一台为平衡机(本例中为23)，另外一台的有功输出为BCC算法中一个控制变量(共1个变量);3区有7个负荷节点，假设其他区域负荷节点功率按照基态潮流输出，3区所有负荷节点的有功和无功分量作为BCC算法的控制变量(共14个变量)。那么控制变量一共15个，相当于细菌要在这15维空间寻优。目标函数相当于细菌食物浓度，各个细菌通过根据自身经验和与同伴的距离选择移动步长和方向。通过寻优后，本文列出一次寻优后各变量的值，见表2。

以23号发电机作为平衡机，在程序运行结果中有功出力为40.93 MW，而13，23节点发电机基态有功分别为37 MW，19.2 MW。因此在不考虑CBM与TRM 前提下，ATC2-3=63.77+40.93 -37 -19.2=48.50 MW。

图3为2-3区运算的收敛特性曲线。从图3可以明显看出，目标函数在32 MW附近出现了短暂的停顿，说明ATC值在此处达到局部最优，传统的Benders算法在此将陷入局部最优，而BCC算法则通过其全局搜索能力跳出这一局部最优。在46 MW附近ATC值爬坡速度变慢，说明此时食物浓度变化小，即梯度变化小。细菌通过运动时间及步长调整，达到了全局最优。2-3区ATC计算30次平均迭代次数为82次，平均值为47.70 MW，最大值为49.72 MW，最小值为46.39 MW，样本标准差为0.9278，说明该算法稳定性较高。

图3 2-3区某次运算收敛特性曲线

4 结 论

本文采用细菌群体趋药性算法求解了基于最优潮流模型的可用输电能力计算模型。针对n维变量寻优问题，提出将n维空间的求解问题化简为(n-1)个二维空间求解，并给出求解此二维空间的表达式;根据ATC计算的寻优特点，引入自适应步长，对迭代过程中的步长和方向自适应调整;针对寻优过程中得到的最优值，引入公告板，使最优值不被随机抛弃。该算法不仅提高了ATC求解的运算速度，同时保证了算法在ATC计算过程中的全局搜索能力。最后，通过IEEE-30节点测试结果验证了该方法在ATC计算中的有效性和合理性。

［1］North American Electric Reliability Council(NERC).Available transfer capability definitions and determination［R］.1996.

［2］李国庆，王成山，余贻鑫.大型互联电力系统区域间功率交换能力研究综述［J］.中国电机工程学报，2001，21(4):20-25.

［3］Gabriel C Ejebe，James G Waight，Manuel Santos-Nieto，William F.Fast Calculation of Linear Available Transfer Capability Tinney［J］.IEEE Trans on Power Systems，2000，15(3):1112 -1116.

［4］GC Ejebe，et al.Available transfer capability calculations［J］.IEEE Transactions on Power Systems，1998，13(4)，1521 -1527.

［5］Xia Yan，Chan Kawing，Liu Mingbo，et al.Calculation of available transfer capability with Transient stability constraints［J］.Proceedings of the IEEE International Conference，2004，1:129 -132.

［6］刘皓明.电力市场环境下计及安全约束的ATC计算方法的研究［D］.南京:南京理工大学，2003.

［7］默哈莫德·夏班，刘皓明，倪以信，等.静态安全约束下基于Benders分解算法的可用传输容量计算［J］.中国电机工程学报，2003，23(8):7-11.

［8］B.Mozafari，A.M.Ranjbar，and A.R Shirani et al.A comprehensive method for available transfer capability calculation in a deregulated power system［R］.IEEE International Conference on Electric Utility Deregulation，Restructuring and Power Technologies(DRPT 2004)，2004，2:680-685.

［9］李国庆，陈厚合.改进粒子群优化算法的概率可用输电能力研究［J］.中国电机工程学报，2006，26(24):18-23.

［10］刘伟.基于智能算法的可用传输能力的对比研究［D］.北京:华北电力大学，2007.

［11］Sibylle D.Muller，et al.Optimization based on bacterial chemotaxis.IEEE Trans on Evolutionary Computation，2002，6(1):16 -29.

［12］李威武，王慧，周志军，等.基于细菌群体趋药性的函数优化方法［J］.电路与系统学报，2005，10(1):58-63.

［13］赵义术，李磊，王大鹏，等.基于细菌群体趋药性的电力系统无功优化［J］.继电器，2005，10(1):50-54.

［14］黄伟，张建华，张聪，等.基于细菌群体趋药性算法的电力系统无功优化［J］.电力系统自动化，2007，31(7):29-33.

［15］Biomimicry of Bacterial Foraging for Distributed Optimization and Control［J］.IEEEControl System Magazine，2002(6):52 -57.

［16］汪峰，白晓民.基于最优潮流方法的传输容量计算研究［J］.中国电机工程学报，2002，22(11):35-40.

［17］吴际舜.电力系统静态安全分析［M］.上海:上海交通大学出版社.1985:5.

［18］黄海涛，等.基于改进粒子群算法的可用输电能力研究［J］.中国电机工程学报，2006 26(20):45-49.

［19］李威武.城域智能交通系统中的控制与优化问题研究［D］.杭州:浙江大学，2003.