概率XM L数据模型的综述

殷丽凤，金 花，田 宏

（大连交通大学 软件学院，辽宁 大连 116028）

在许多应用中，如传感器网络[1]、无线射频识别技术[2]、数据集成[3]、基于位置的服务[4]等领域都涉及不确定数据。不确定数据普遍存在，传统的数据管理技术无法有效管理不确定性数据，不确定数据的管理技术成为新的研究领域。针对不确定数据的研究工作已有几十年的历史，自二十世纪八十年代末开始，针对概率数据库的研究工作从未间断，研究者把概率信息引入关系数据模型中（称为概率关系数据库），对其概率关系数据模型、概率关系代数、查询技术、查询优化、集成技术等领域进行了研究[5-10]，如今该类数据库的管理技术取得了很大进展。

随着网络应用的快速发展，可扩展标识语言XML（eXtensible Markup Language）已成为Internet上信息表示和数据交换的标准，在网络服务、电子商务、电子数据交换、科学数据表示、数据建模与分析、智能体和搜索引擎等领域得到了广泛的应用，XML技术也日益受到更广泛的关注，XML数据库的管理技术也不断得到成熟和完善。由于不确定数据的普遍存在性，通常不确定信息以概率信息的形式在XML中表示，因此，研究表示和处理概率XML数据成为一个新的研究领域。XML的半结构化、自描述性好及可扩展性高等优点使其在概率数据表示上比概率关系模型占优势。因此，近些年概率XML数据管理技术成为研究热点。文中综述了概率XML数据、概率XML数据模型以及不同模型之间的转换关系等方面的工作，讨论目前存在的主要问题和进一步的研究方向。

1 概率XM L数据

XML数据通常可以用文档树来描述，概率XML数据是把概率信息加入到文档树中，称为概率XML文档树。在概率XML文档树中，包含两种类型的节点，一种为普通节点，描述实际的数据；一种为分布节点，描述概率数据。为了描述不同离散类型和连续类型的概率分布，分布节点分为以下6种类型。

1）独立类型节点ind[11-12]，ind节点的孩子节点在概率XML文档树中的出现是独立的，不受其他节点影响。若ind节点v选择孩子w的概率为p（w），则v选择孩子的子集C的概率为，表示v的孩子不在C中的节点集合。

2）互斥类型节点mux[11-12]，mux节点的孩子节点只能出现一个，或者全不出现。若mux节点v的孩子w1，…，wn的概率分别为 p（w1），…，p（wn），满足（wi）≤1。 节点 v 的孩子全不出现的概率为1-（wi）。

3）事件驱动类型节点cie[13-14]，cie节点的存在是由独立的外部事件变量e1，…，em决定的，外部事件变量e1，…，em的发生与否决定cie节点的存在性。

4）组合类型节点exp[15-16]，exp节点有多个孩子节点，可以选择不同的孩子节点组成exp的孩子节点的集合，若exp的孩子节点的不同子集 c1，c2，…，cn的概率分别为 p（c1），p（c2），…，p（cn），要求

5）确定类型节点det，det节点的孩子节点必须全部出现。它是上面4种类型节点的特例。

6）连续概率分布节点cont[17]，cont节点描述了此节点服从的连续概率分布，如二项分布，泊松分布，高斯分布，正态分布等。

以上前5种类型节点描述了离散类型的不同概率分布，第6种类型节点描述了连续概率分布。根据解决问题的实际需要，研究者采用这6种类型节点进行组合，提出了不同的概率XML数据模型。

2 概率XM L数据模型

为了解决不同问题的实际需要，研究者提出包含不同类型分布节点的概率 XML 数据模型，我们用 PrXML{type1，type2，…}表示此通用模型，type1，type2分别表示上面六种分布节点类型中的任一种类型。例如PrXML{ind，mux}表示只包含独立节点和分布节点的概率XML数据模型。

在概率XML数据模型PrXML{ind，mux}[11-12]中，各节点的概率依赖于其父亲节点的概率，节点之间的关系可以是互斥关系（mux）或相互独立（ind）关系。图1描述了该模型的一个例子。有5个普通节点，2个分布节点，节点B、C之间相互独立，概率值分别为0.7和0.8，节点D、E之间相互互斥，概率值分别为 0.6 和 0.3。 此时仅包含 A、C、D 的子树概率为（1-0.7）×0.8×0.3=0.072；任意子树均不能同时包含D和E两个节点。

在概率XML数据模型PrXML{cie}[13-14]中，它并不在各个节点或边上附加概率值来描述不确定性，而是在各个节点上附加一系列事件变量，节点的存在性由外部事件是否发生来决定。图2描述了一个PrXML{cie}的例子，共有2个外部事件w1和w2，其发生的概率分别为0.8和0.7。节点C出现的前提条件是w2发生，而节点D出现的前提条件是w1发生而w2不发生。节点C和D的存在条件为互斥，从而不存在同时包含C和D的子树。包含A、B、D 3个节点的子树的概率为：0.8×（1-0.7）=0.24。 可以看出 PrXML{cie}的表达能力比 PrXML{ind，mux}强。

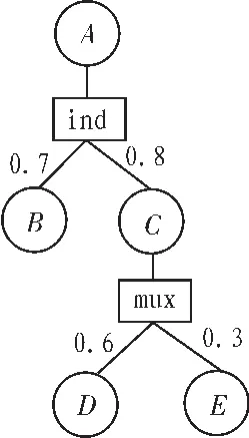
图1 PrXML{ind， mux}模型Fig.1 Model of PrXML{ind，mux}

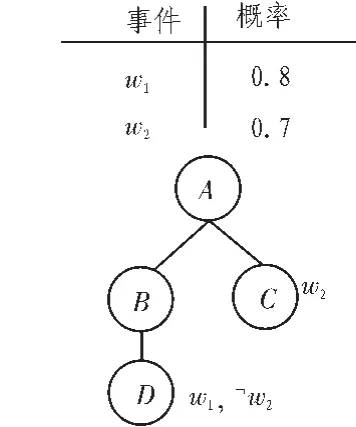
图2 PrXML{cie}模型Fig.2 Model of PrXML{cie}

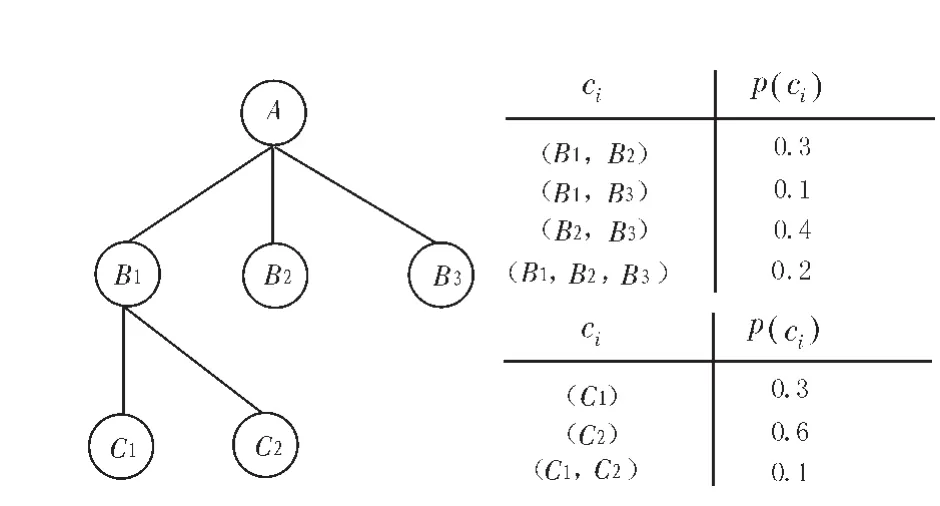
图3 PrXML{exp}模型Fig.3 Model of PrXML{exp}

在概率XML数据模型PrXML{exp}[15-16]中，每个节点可以选择孩子节点的任意组合。文中对文献[15]、[16]中的图约束为树，把区间概率变为点概率，给出图3描述概率XML数据模型PrXML{exp}的一个例子。此图共有6个节点，节点A和B1属于组合类型节点，节点A可以选择孩子节点B1、B2、B3的组合中{（B1，B2）（B2，B3）、（B1，B3）、（B1，B2，B3）}中的任意一个组合，节点 B1可以选择孩子节点 C1、C2的组合中{（C1）、（C2）、（C1，C2）}中的任意一个组合。若节点A选择孩子节点组合（B1，B3）而节点B1孩子节点组合（C2）构成的子树概率为0.1×0.6=0.06。

B Kimelfeld等人[18]提出了包含cie、exp节点的概率XML数据模型 PrXML{cie，exp}。 E Kharlamov 和 S Abiteboul等人[17]对前面介绍的概率XML数据模型进行了扩展，允许叶子节点为cont节点，表示连续概率分布，如二项分布，泊松分布，高斯分布，正态分布等。这样此模型具有很强的通用性。

3 概率XM L数据模型的转换

可能世界模型是不确定数据库应用的最广泛的模型，上面介绍的概率XML数据模型PrXML{type1，type2，…}构成了概率XML数据库的可能世界[19]。在该模型中，通过下面两个步骤可得到一个可能世界的实例，实例的概率值可以通过分布节点固有的特征计算得到。

1）随机选择每个分布节点的合法孩子节点，删除没有选择的所有孩子节点及其后裔。

2）删除所有的分布节点。如果普通节点v没有父亲节点，选择离v最近、合适的普通祖先节点为新的父亲节点。

通过反复使用上面两个步骤可以得到可能世界的所有可能世界实例，且满足所有可能世界实例的概率总和为1。一般情况下，可能世界实例的数量远远高于概率XML数据库的规模，甚至是后者的指数倍，这也是概率XML数据库管理技术所面临的最大难点。

根据解决实际问题的需要，根据上面前五种不同类型分布节点的不同组合，可以提出不同的概率XML数据模型，Benny Kimelfeld等人[20]根据这些模型表达力研究了这些模型之间的相互转换关系，如图4所示。

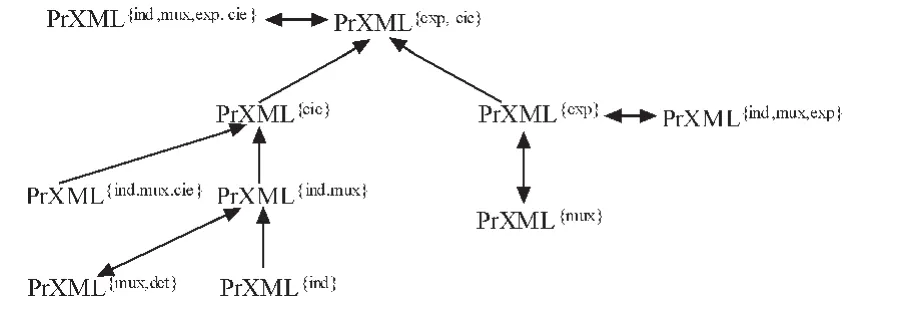
图4 PrXML模型转换的有效图Fig.4 PrXML effective model transformation diagram

从图4可以看出，模型PrXML{ind}与PrXML{mux}之间不能相互转换，模型PrXML{exp}与PrXML{cie}之间也不能相互转换，但其它所有模型都可以转换为 PrXML{exp，cie}，从而 PrXML{exp，cie}的表达力最强，而PrXML{ind}、PrXML{mux}的表达力最弱。针对前面介绍的六种分布节点类型，我们可以把cont类型节点加入到概率 XML 数据模型 PrXML{type1，type2，…}中，对概率 XML 数据模型之间的转换关系进行扩展，如图5所示，从而进一步增强表达能力。

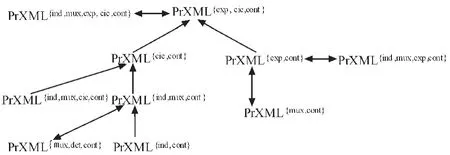
图5 扩展的PrXML模型转换有效图Fig.5 Extended PrXML effective model transformation diagram

4 结束语

人类认知存在的局限性、度量的误差、数据的动态变化以及信息描述的差异等情况，往往会产生许多不确定的数据。不确定数据在诸如军事、经济、物流、电信、金融等领域的具体应用中也普遍存在。针对不确定数据管理技术的研究已有40年的历史，概率关系数据库管理技术取得了很大的进展。随着网络技术的发展，XML成为Internet上信息表示和交换的标准。XML的半结构化、自描述性好及可扩展性高等优点，使其在概率数据表示上与概率关系模型相比较占优势。因此，近些年概率XML数据管理技术成为研究热点。概率XML数据管理技术与确定性的XML数据管理技术截然不同，这使得前者面临如下挑战：

1）庞大的可能世界实例集合。与概率关系数据库相同，概率XML数据管理所面临的直接挑战就是其相当于XML数据库规模呈指数倍的可能世界实例的数量。因此，在查询时需要考虑删除概率值太小的实例后查询还是直接在所有可能世界实例上查询之间进行权衡。

2）概率信息。概率信息在概率XML数据管理中具有多重角色。在查询时，输入的文档有概率信息，描述文档中有不确定信息；输出的文档有概率信息，描述查询结果的发生概率；查询定义可以有概率信息，用于约束查询结果。因此，概率信息的出现极大地改变了确定XML数据的处理方式，迫切新技术进行处理。

在概率XML数据库管理领域仍有很多工作有待完成。

1）许多确定性XML数据管理领域所遇到的问题在概率XML数据管理领域也非常重要，需要为之寻求相应的解决方案。

2）由于概率信息的存在，概率XML数据管理领域存在一些特有的查询问题，需要找出这些查询并给出相应的解决方案。

3）概率 XML数据的约束[20]、集成、挖掘也有待进一步研究。

[1]Deshpande A，Guestrin C，Madden S，et al.Model-driven data acquisition in sensor networks[C]//Proceedings of the 30th international conference on Very large data bases，2004:588-599.

[2]许嘉，于戈，谷峪，等.RFID不确定数据管理技术[J].计算机科学与探索，2009， 3（6）:561-576.XU Jia，YU Ge，Gu YU，et al.Uncertain data management technologies in RFID[J].Journal of Frontiers of Computer Science and Technology，2009，3（6）:561-576.

[3]Madhavan J，Cohen S，Xin D，et al.Web-scale data integration:you can afford to pay as you go[C]//Roceedings of the 3rd biennial conference on innovative data systems research，2007:342-350.

[4]LIU Ling.From data privacy to location privacy:models and algorithms （tutorial）[C]//Proceedings of the 33rd international conference on very large data bases，2007:1429-1430.

[5]Cavallo R，Pittarelli M.The theory of probabilistic databases[C]//Proceedings of the 13th International Conference on Very Large Data Bases，1987:71-81.

[6]Barbara D，Garcia-Molina H，Porter D.The management of probabilistic data[J].IEEE Transactions on Knowledge and Data Engineering，1992， 4（5）:487-502.

[7]Fuhr N，Rolleke T.A probabilistic relational algebra for the integration of information retrieval and database systems[J].ACM Transactions on Information Systems，1997，15（1）:32-66.

[8]Zimanyi E.Query evaluation in probabilistic databases[J].Theoretical Computer Science，1997，171（1-2）:179-219.

[9]Dalvi N，Suciu D.Management of probabilistic data foundations and challenges[C]//Proceedings of the 26th ACM SIGMODSIGACT-SIGART symposium on principles of database systems.2007:1-12.

[10]Pei J， Hua M， Tao Y F， Lin X M.Query answering techniques on uncertain and probabilistic data:tutorial summary[C]//Proceedings of 2008 ACM SIGMOD international conference on management of data.2008:1357-1364.

[11]Nierman A，Jagadish H V.ProTDB:Probabilistic data in XML[R].Hong Kong：In Proc of the 28th VLDB conference，2002.

[12]LI Te，SHAO Qi-hong，CHEN Yi.PEPX:A query-friendly probabilistic XML database[C]//Proceeding of the 15th ACM international conference on information and knowledge management.ACM Press，2006:848-849.

[13]Abiteboul S，Senellart P.Querying and updating probabilistic information in XML[C]//Proceedings of the 9th international conference on Extending database technology:Advances in database technology.2006:1059-1068.

[14]Senellart P，Abiteboul S.On the complexity of managing probabilistic XML data[C]//Proceedings of the 26th ACM SIGMOD-SIGACT-SIGART symposium on principles of database systems，2007:283-292.

[15]Hung E，Getoor L，Subrahmanian V S.PXML:a probabilistic semistructured data model and algebra[C]//Proceedings of the 19th IEEE international conference on data engineering.bangalore，2003:467-478.

[16]Hung E，Getoor L，Subrahmanian V S.Probabilistic interval XML[J].ACM Transactions on Computational Logic， 2007，8（4）:24.

[17]Abiteboul S，Chan T-H H，Kharlamov E.Aggregate queries for discrete and continuous probabilistic XML[C]//Proceedings of the 13th international conference on database theory，2010:50-61.

[18]Kimelfeld B， Kosharovsky Y，Sagiv Y.Query evaluation over probabilistic XML[J].VLDB Journal， 2009，18（5）：164-170.

[19]CHANG L J，YU J X，QIN L.Query ranking in probabilistic XML data[C]//In Proc of the 12th EDBT Confer-ence，Saint-Petersburg，Russia，2009:156-167.

[20]Kimelfeld B， Kosharovsky Y，Sagiv Y.Query efficiency in probabilistic XML models[C]//In SIGMOD conference，2008:710-714.

[21]Cochen S，Kimelfeld B，Sagiv Y.Running tree automata on Probabilistic XML[C]//In proc.PODS，RI，2009:227-236.