RLC二阶电路暂态过程的M ultisim仿真
祁国权
(渤海大学 数理学院物理系,辽宁 锦州 121000)
RLC二阶电路暂态过程是当电源接通或断开的瞬间,电路中的电流或电压非稳定的变化过程,有过阻尼、临界阻尼、欠阻尼等几种情况[1-2]。
用Multisim仿真软件[3-8]进行RLC二阶电路暂态过程工作过程波形仿真分析,以虚拟仪器中的函数信号发生器做实验中的信号源产生所需的方波信号模拟电源接通或断开,以示波器显示输入信号、输出信号波形,可直观描述电路的暂态过程工作过程。
以下分析用Multisim10版本。
1 仿真原理
1.1 仿真电路的创建及求解响应的微分方程
在Multisim10中创建的RLC二阶电路暂态过程仿真电路如图1所示。其中函数信号发生器XFG1用作信号源产生方波信号,从其面板图的“+”、“Common”端输出正极性信号,方波信号的占空比为50%。方波信号幅度为U的半周测试电路的零状态响应(对应RLC电路的充电过程)、方波信号幅度为0的半周测试电路的零输入响应(对应RLC电路的放电过程),设置幅度U=2 V。示波器XSC1用于显示信号源产生的方波信号及电容两端电压uC(t)的波形。
RLC二阶电路由电阻R、电感L及电容C串联构成,元件参数的选取为电感L=10 mH、电容C=10 nF,电阻R跟据过阻尼、欠阻尼及临界阻尼条件确定。

图1 RLC二阶仿真实验电路创建Fig.1 The creation of RLC second order simulation experimental circuit
选取电容两端电压uC(t)为响应变量,则可建立如下求解零状态响应及零输入响应的微分方程[1-2]:
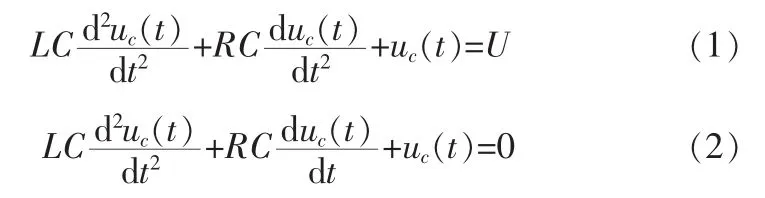
方程(1)、(2)的解,在欠阻尼、临界阻尼及过阻尼 3种情况下是不同的。
1.2 欠阻尼情况分析及Multisim仿真
电路参数满足式(3)为欠阻尼的情况[1-2]。

式(1)微分方程的零状态响应为:
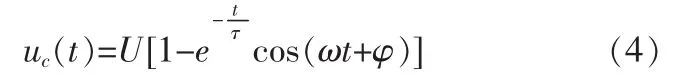
式(2)微分方程的零输入响应为:
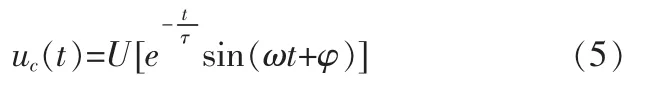
其中时间常量

式(4)、(5)表明,uc(t)响应为振幅衰减的正弦振荡过程。
振荡角频率为:

若在方波输入信号的一个周期内能观测uC(t)欠阻尼情况的零状态及零输入响应波形,方波信号的周期T应满足式(8):

依式(3)、(8),选取电阻 R=200 Ω、方波信号周期 T=1 μs(f=1 000 Hz)时Multisim仿真波形如图2所示,其中由上至下依次是输入方波信号、uC(t)的波形,仿真结果反映了式(4)、(5)的变化规律。
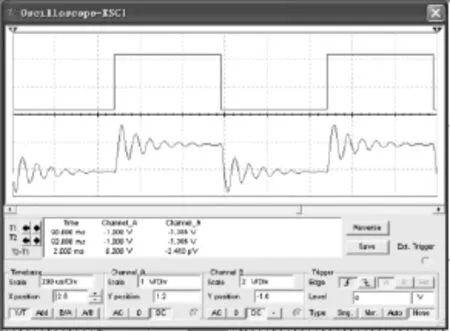
图2 欠阻尼情况的Multisim仿真波形Fig.2 Multisim simulation waveforms under the underdamped case
1.3 临界阻尼情况分析及Multisim仿真
电路参数满足式(9)为临界阻尼的情况[1-2]。

式(1)微分方程的零状态响应为:
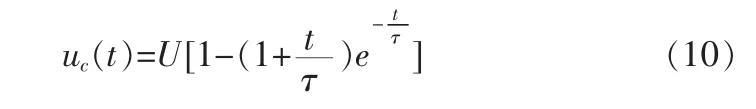
式(2)微分方程的零输入响应为:
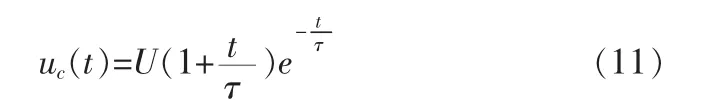
时间常量τ的表达形式同式(6)。
式(10)、(11)表明,uc(t)响应为欠阻尼振荡刚刚不出现振荡的状态。
若在方波输入信号的一个周期内能观测uC(t)临界阻尼情况的零状态及零输入响应波形,方波信号的周期T应满足式(12):

依式(9)、(12),选取电阻 R=2 kΩ、方波信号周期T=200 μS(f=5 000 Hz)时 Multisim 仿真波形如图 3所示,其中由上至下依次是输入方波信号、uC(t)的波形,仿真结果反映了式(10)、(11)的变化规律。
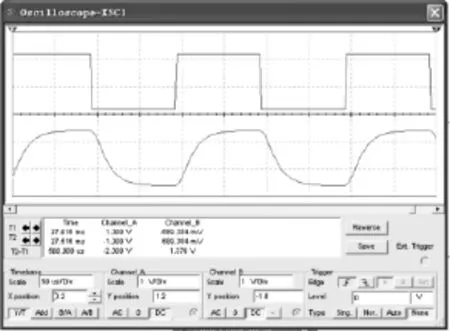
图3 临界阻尼情况的Multisim仿真波形Fig.3 Multisim simulation waveforms under the critically damped case
1.4 过阻尼情况分析及M ultisim仿真
电路参数满足式(13)为过阻尼的情况[1-2]。

式(1)微分方程的零状态响应为:
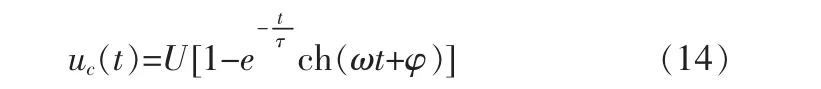
式(2)微分方程的零输入响应为:
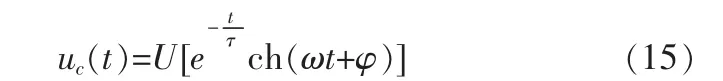
时间常量的表达形式同式(6)。
式(14)、(15)表明,uc(t)响应为不出现振荡的状态。
若在方波输入信号的一个周期内能观测uC(t)过阻尼情况的零状态及零输入响应波形,方波信号的周期T应满足式(12)。
依式(13)、(12),选取电阻 R=3 kΩ、方波信号周期 T=1 μs(f=1 000 Hz)时Multisim仿真波形如图4所示,其中由上至下依次是输入方波信号、uC(t)的波形,仿真结果反映了式(14)、(15)的变化规律。

图4 过阻尼情况的Multisim仿真波形Fig.4 Multisim simulation waveforms under the overdamped case
2 结束语
用硬件实验仪器对电路暂态过程进行测试、描述工作过程时,仪器输出参数调整较为繁琐,信号频率偏高或偏低时波形显示不稳定。用Multisim软件仿真解决了这一问题,将计算机仿真软件Multisim引入到电路实验中,使电路的分析、仿真、测试非常方便,特别便于电路参数改变时的测试。所述方法具有实际应用意义。
将电路的硬件实验方式向多元化方式转移,利于培养知识综合、知识应用、知识迁移的能力,使电路分析更加灵活和直观。
[1]符时民,陈维石,封丽.基础物理实验(第三册)[M].沈阳:东北大学出版社,2007.
[2]杨述武.普通物理基础(电磁学部分)[M].北京:高等教育出版社,2000.
[3]郑步生,吴渭.Multisim2001电路设计及仿真入门与应用[M].北京:电子工业出版社,2002.
[4]任骏原.用Multisim仿真软件分析触发器的状态变化过程[J].实验科学与技术,2011,9(1):53-56.REN Jun-yuan.The state transition analyzing of flip-flop by multisim[J].Experiment Science&Technology,2011,9(1):53-56.
[5]任骏原.Multisim在触发器工作波形分析中的应用[J].现代电子技术,2010,33(15):184-186.REN Jun-yuan.An application of Multisim to the working wave analyzing of Flip-flop[J].Modern Electronics Technique,2010,33(15):184-186.
[6]任骏原.数字电子技术实验教学模式的改革与实践 [J].渤海大学学报:自然科学版,2010,31(2):l65-167.REN Jun-yuan.The reformation and practice of digital electronics practice teaching mode[J].Journal of Bohai University:Natural Science Edition,2010,31(2):l65-167.
[7]任骏原.74LS161异步置零法构成任意进制计数器的Multisim仿真[J].电子设计工程,2011,19(14):135-137.REN Jun-yuan.Multisim simulation for Modulo-N counter composed by 74LS161 with asynchronous reset method[J].Electronic Design Engineering,2011,19(14):135-137.
[8]任骏原.电子技术课程CAI教学模式的探索与实践[J].电气电子教学学报,2009,31(4):99-100.REN Jun-yuan.The exploring and practice of CAI teaching mode of electronics technology course[J].Journal of Electrical&Electronic Education,2009,31(4):99-100.

