配变三相不平衡全电容调节补偿的研究

汪 蕾

（南京供电公司，江苏南京 210019）

目前，我国的配电网主要采用三相四线制的配电方式，配电变压器一般为Y/Yn0接线方式。在理想的情况下，配电网三相负荷应配置均衡，配电变压器处于对称运行状态，而实际上由于在配电网用户端存在着大量的单相负荷，且各类负荷使用不具同步性，往往会造成配电系统处于三相不平衡状态，使配变处于绝对不对称运行状态。由于配变的不对称运行，将会在配电网中产生相应的负序电流和零序电流，产生的负序电流和零序电流会严重影响供电质量，威胁电网安全运行[1]。

1 传统低压无功补偿装置的补偿方法

通过对南京供电公司某片区587台配电变压器监测仪采集的数据显示，经统计约有57.58%的公用配电变压器不平衡度超过了20%，三相不平衡度分布情况如表1所示。不平衡度变大，不仅引起低压配电网功率因数低下，而且带来了损耗的增大。

表1 某片区配变三相不平衡分布情况

目前应用较广的低压无功补偿装置一般采用三相共补、单相分补、共补与分补结合的3种电容补偿方法，共补是指三相同时投入等容量的三角形接法补偿电容，分补是指在各相投入星形接法的补偿电容[2]。传统低压无功补偿装置采用共补分补混合补偿的方法，其原理是：系统三相功率因数偏低时，先投入等容量的共补电容，若在共补电容投入后，某相功率因数还是偏低，则在不过补偿的情况下，各相再分别投入分补的电容进行补偿。该补偿方法虽然可以补偿无功，但由于其接在相与相间的共补电容是等量的，不能达到转移有功电流的目的，所以无法对三相不平衡度进行调节。为了达到既补偿无功，又调节三相不平衡的双重目的，应用一种全电容的调节补偿模型，并对此进行优化，达到了很好的调节补偿效果。

2 三相不对称调节补偿方法及模型

2.1 三相不对称调节补偿的基本原理

三相不对称调补方法与共补分补混合补偿方法的差异在于接在相与相间的电容是不等量的，它的基本原理是利用负荷中的电感，通过适当地在相与相之间、相与零线之间接入不等容量的电容，从而实现在补偿系统功率因数的同时，又可调整三相负荷的不平衡度[3，4]，其工作原理如图1所示。

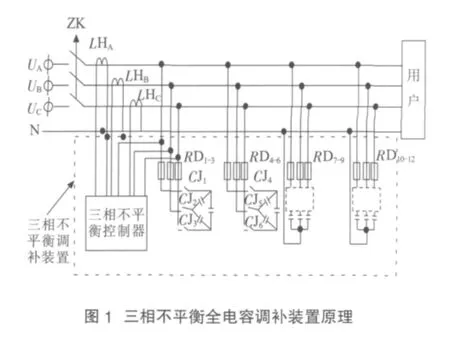
2.2 三相不对称调补模型

在三相四线制的电压配电网络中，假设变压器低压出线端的三相电压幅值相等，相位相差120°，即：

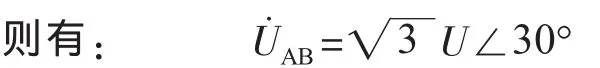
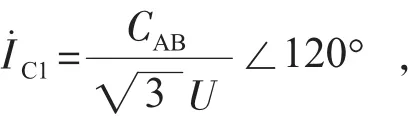
对于B相、C相，同理可推导得到加在BC，CA相间的电容量CBC，CCA对应相所转移的有功功率量和补偿的无功功率。

设定Pa，Pb，Pc分别为调补前的各相有功功率；Qa，Qb，Qc分别为调补前的各相无功功率；PA，PB，PC分别为调补后的各相有功功率；QA，QB，QC分别为调补后的各相无功功率。则可以得到：

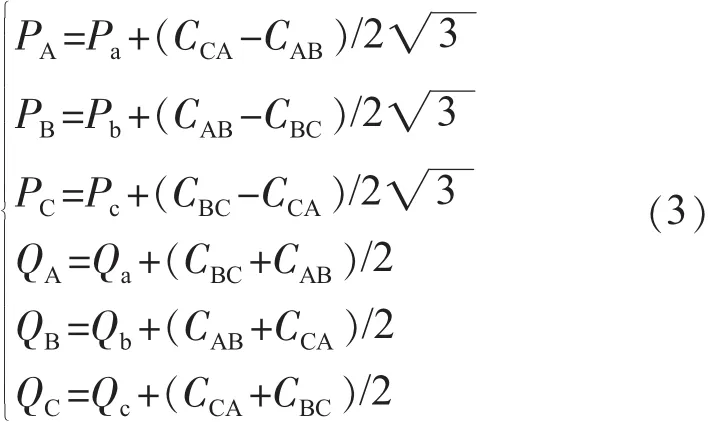
CAY，CBY，CCY分别为加在 A，B，C 各相的电容量，其分别补偿了各相的无功功率，代入式（3）得到最终调补模型为：

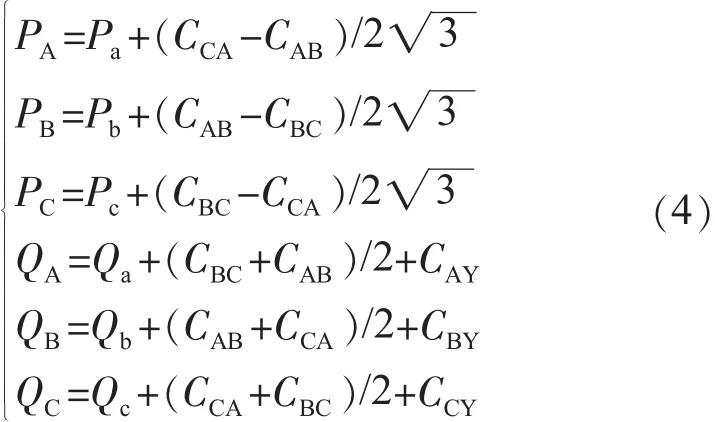
2.3 优化模型的建立

在三相四线制的配电网中，可将中线电流表示为各相电流的矢量和以及配变运行时的总损耗。根据系统运行指标要求，可以确定以配变损耗最小为目标对调补模型进行优化，并相应地建立目标函数。该目标函数为：

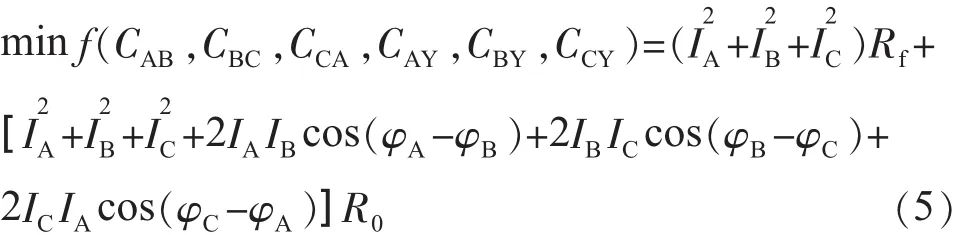
式（5）中：Rf为绕组电阻；R0为零序电阻。

结合实际加在各相中和各相间的电容量是有限制的情况，可以得到调补模型的约束条件为：

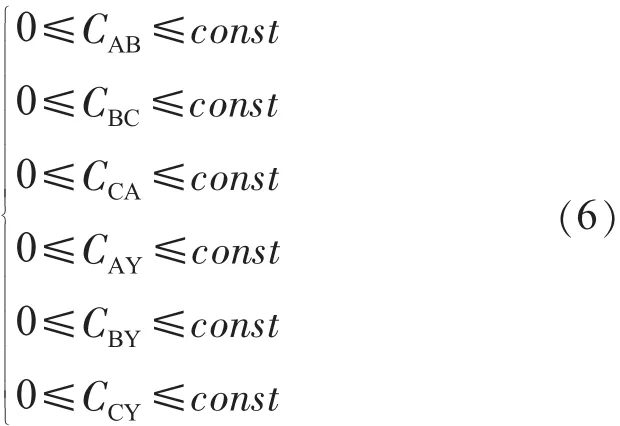
式（6）中：const为一个常数。

在实际应用中还要求各相投入的电容量不得过补偿，所以调补模型还必须满足以下条件：

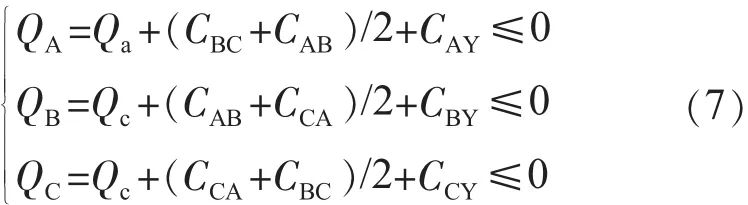
从上述模型可见，式（5）的目标函数是非线性的。因此，该优化模型是带约束条件的非线性最优化的问题。

3 算例优化与仿真验证

3.1 算例优化

在理论推导的基础上，利用MATLAB软件中的fmincon函数来求多变量有约束非线性函数的最小值[5]。

（1）算例1。某一型号为S11-315 kVA/10 kV的配电变压器，其零序电阻R0=0.121 Ω，绕组电阻R1=0.008 50 Ω，其低压侧调补前各相的有功功率、无功功率分别为：

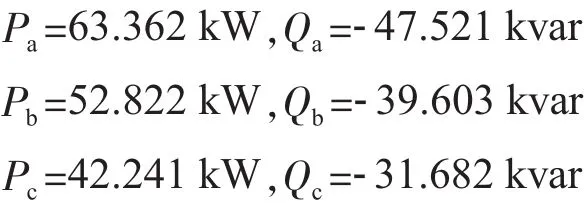
假定加在各相中的星形电容量为25.00 kvar，各相间的三角形电容量为39.00 kvar，即调补模型约束条件为：

为了各相投入的电容量不过补偿还需满足式（7）条件。现把上述的约束条件输入fmincon函数，得到的优化结果为：

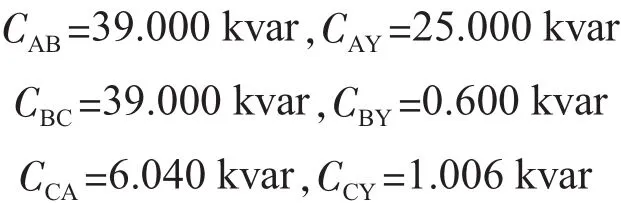
因实际应用中的电容器组一般为整数，则：

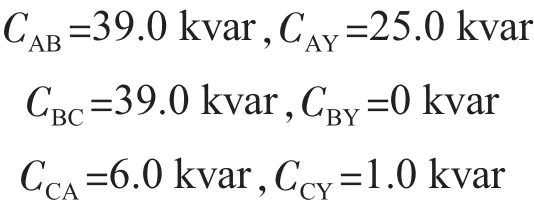
（2）算例2。基于算例1的原始数据，改变了其低压侧调补前各相的有功功率、无功功率，而在其他约束条件不变时，改变后的功率不平衡度比算例1更大。

经把约束条件输入fmincon函数，得到的优化结果为：

因实际应用中的电容器组一般为整数，则：

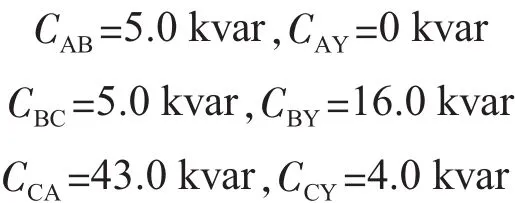
3.2 仿真验证

利用MATLAB的SIMULINK工具箱进行仿真来验证以上优化结果的正确性，算例1中A相有功功率、无功功率变化的仿真结果如图3所示。调补前后的网损变化的仿真结果如图4所示。

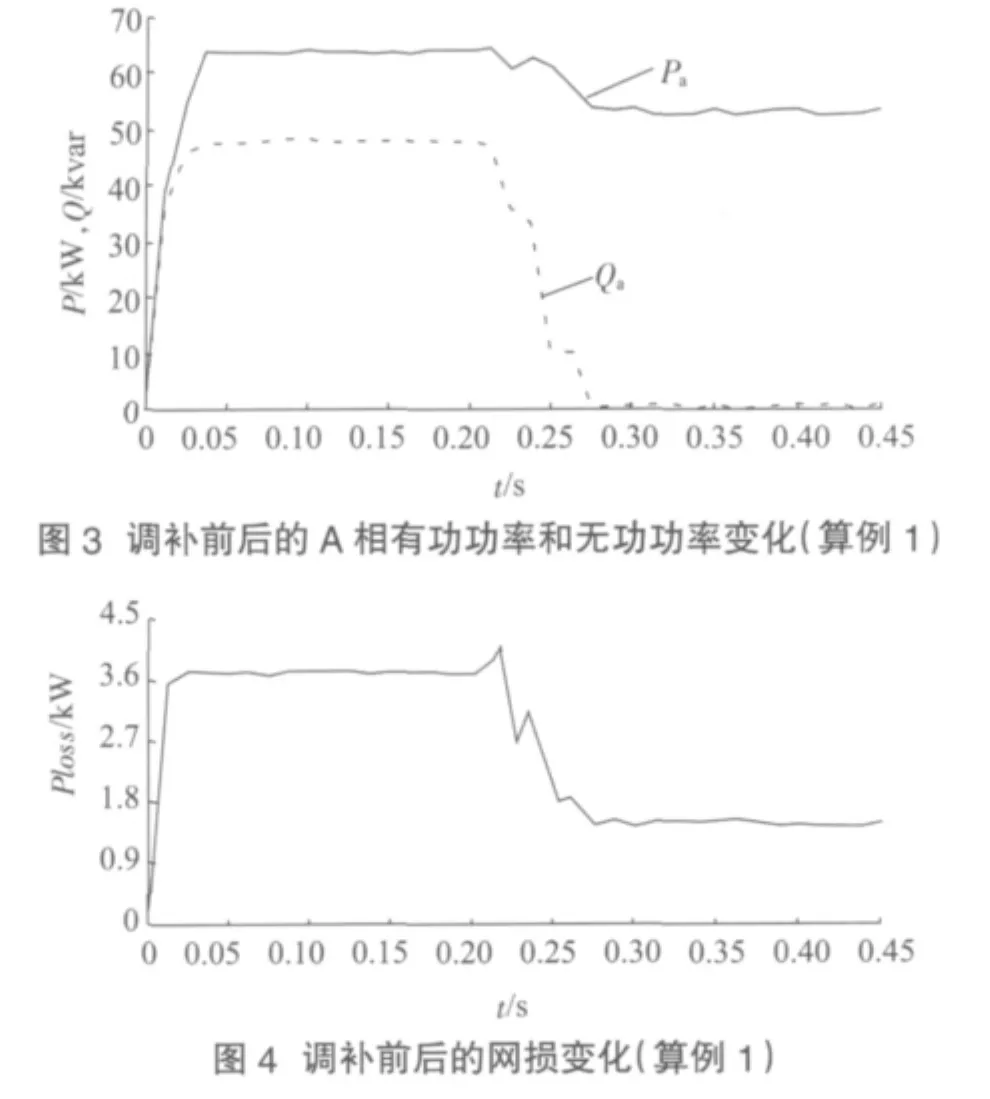
通过图3可以看出，A相在0.2 s进行调补后的无功基本降到0，达到了补偿的目的，同样可对B相、C相进行仿真，通过仿真结果不难看出，补偿后的三相有功功率基本相同。根据前面的分析可知，在三相基本对称的情况下网损可以达到最小。由图4可见，在0.2 s前未进行调补时，网损均在3.6 kW以上，进行调补后网损基本稳定在1.6 kW左右。该仿真结果验证了理论推导和优化结果的正确性。算例2的仿真结果如图5、图6所示。

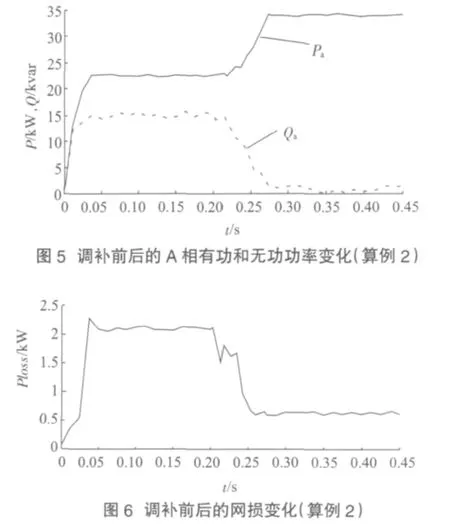
由图5、图6可见，虽然本算例的负荷不对称度很大，但调补后的三相有功功率仍基本相同，三相无功功率也只有很小的波动，网损则大幅度下降。

4 与共补分补方法的比较

根据共补分补方法的原理，结合上节中算例1的数据，得出各相中和相间的共补分补的电容量为：

利用得出的各相中和相间的补偿电容量值，对上述配电变压器低压侧在补偿电容量前、共补分补和调补后的各参数指标进行比较，比较结果如表2所示。

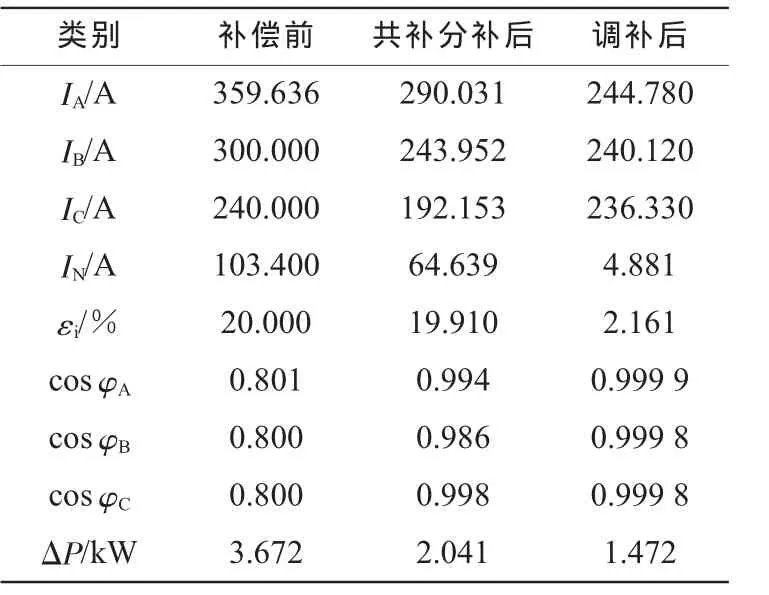
表2 算例1不平衡补偿前和共补分补后及调补后结果比较

表2中，εi为三相不平衡度。从表2中的数据可以看出，采取共补分补后，功率因数得到了很大提高，但三相不平衡度基本没有得到调整，补偿前为20%，补偿后为19.9%；采取调补后，不仅功率因数得到很大的提高，而且三相不平衡度从补偿前的20%显著下降到2.17%；还有对于配变损耗，调补比共补分补减少了0.569 kW，因此调补的效果十分的明显。

根据共补分补方法的原理，结合上节中算例2的数据，算出了各相中和相间的共补分补的电容量且为：

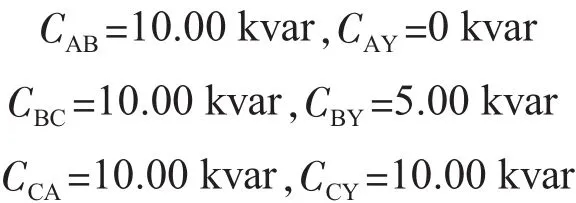
利用得出的各相中和相间的补偿电容量值，对上述配电变压器低压侧在补偿电容量前、共补分补和调补后的各参数指标进行比较，比较结果如表3所示。

由表3可见，算例2补偿前的三相不平衡度达到32.28%，采用共补分补后只略有改变，三相不平衡度为32.05%，而采用三相不平衡全电容补偿的优化方法的三相不平衡度仅为1.60%。可见该方法对功率不平衡度大的有效性。

表3 算例2不平衡补偿前和共补分补后及调补后结果比较

5 结束语

针对三相四线制的低压配电网三相不平衡，并根据配电网中实际负荷大都为感性负荷的情况，结合无功补偿尽量只使用电容、而不使用电感的原则,利用矢量分析法，分析得出全电容调补模型，根据全电容调补模型，以损耗最小为优化目标得出调补的电容量，再通过仿真验证其正确性，最后通过不平衡补偿前、共补分补后、调补后几种情况下各参数的数据比较，可以清晰地看出全电容调补不仅补偿了无功，而且三相不平衡度也显著下降，配变损耗也明显降低，充分体现了其优越性。但由于受电容容量的限制，实际控制中无法根据理论计算的电容补偿值进行准确的补偿，因此这种控制是有级差的控制,只能在电容器组容量配置有限的条件下找到一种最接近的投切控制方案。如何尽量做到有电容可投，电容配置如何细分，这还需要进一步的研究。

[1]杨云龙，王凤清.配电变压器三相不平衡运行带来的附加损耗、电压偏差及补偿方法[J].电网技术，2004，28(8)：73-76.

[2]范 斌,孟文博，徐正光.三相非对称系统对称化补偿的研究[J].微计算机信息，2007，23(19)：294-295.

[3]王 焕，王永强.低压无功补偿装置的探讨[J].电气制造，2008(12)：60-62.

[4]张永军，孟文博.三相不平衡与无功功率综合补偿系统的研究[J].电工技术杂志，2004(12).

[5]苏金明，阮沈勇.MATLAB实用教程[M].北京：电子工业出版社，2008.