单气室油气弹簧的优化设计研究

李占芳，仝军令，李 威

(1.中国矿业大学 应用技术学院，徐州 221008;2.吉林大学 汽车动态模拟国家重点实验室，长春 130022;3.中国矿业大学 机电工程学院，徐州 221116)

油气悬架是一种新型的悬架形式，它的核心部件是油气弹簧。油气弹簧集弹性元件和阻尼元件于一体，以油液作为传力介质，用气体作为弹性介质，具有良好的非线性刚度和阻尼特性，因此在工程车辆、军用车辆、大型矿用自卸车及高级轿车上得到了广泛的应用。油气弹簧起源于国外，因此，国外在油气弹簧的研究方面已日趋成熟，他们已经掌握了从油气弹簧的设计、生产到维护的一系列技术。而国内的研究起步较晚，国内绝大多数关于油气弹簧的研究都是针对具体结构类型的油气弹簧进行建模、仿真、试验和特性分析，目的在于为油气弹簧的设计奠定理论基础，但国内至今仍然没有形成一套简单易行、切实可靠的油气弹簧的设计方法［1］。由文献［2，3］的研究可以知，油气弹簧的各项参数对悬架系统性能的影响非常复杂，因此对油气弹簧主要参数的设计是一个复杂的过程，需要统筹考虑。很显然，采用传统的设计方法难以有效、合理地确定出油气弹簧的主要参数，而优化设计方法则可以很好地在各目标之间寻求最佳的折中，从而有助于合理地确定出油气弹簧的主要参数。而且油气弹簧的优化设计也是近年来有关油气弹簧的主要研究方向之一［1］。

优化设计主要工作包括两部分内容［4］。首先要将设计问题的物理模型转变为数学模型，然后采用适当的最优化方法求解数学模型。本文以某军用越野车为例，建立了其油气悬架系统1/2车辆模型。在此基础上，讨论了1/2车辆模型的油气弹簧优化设计数学模型的建立，并应用粒子群算法进行了求解。

1 油气悬架系统数学模型的建立

1.1 油气弹簧单缸数学模型的建立

图1所示为应用于某军用越野车的油气弹簧的结构简图。该油气弹簧主要由悬架缸，主活塞，蓄能器，浮动活塞和中空的活塞杆组成。主活塞与悬架缸构成了主油室Ⅰ，浮动活塞把活塞杆内的空腔分为副油室Ⅱ和副气室Ⅲ，蓄能器的气囊为气室Ⅳ。

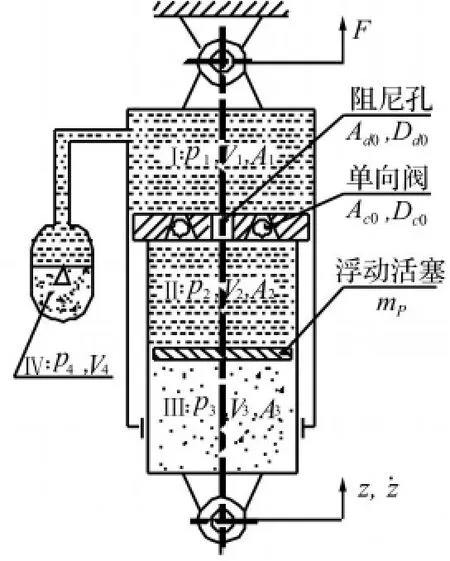
图1 油气弹簧结构简图Fig.1 Diagram of hydro-pneumatic spring

为了获得油气弹簧的输出力特性，需要建立油气弹簧的单缸数学模型。油气弹簧单缸数学模型的建立过程参见文献［2］，其结果如式(1)～式(8)所示。

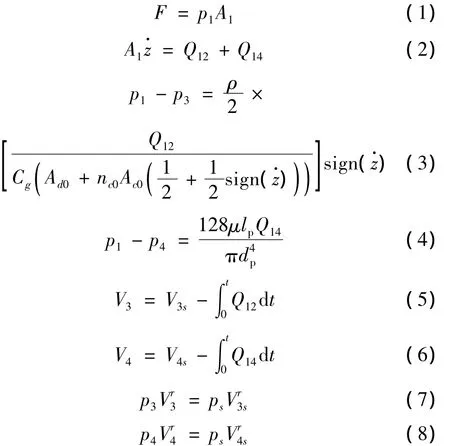
式中:F为悬架缸输出力/N;p1为主油室Ⅰ腔内的压力/Pa;A1为主活塞的横截面积/m2;z为活塞—活塞杆组件相对于悬架缸的位移/m;Q12、Q14为主油室流入副油室、蓄能器的流量，流入为正，流出为负/(m3·s－1);p3为副气室内的压力/Pa;ρ为液压油的密度/(kg·m－3);Cg为流量系数;Ad0为阻尼孔过流面积/m2;nc0为单向阀的个数;Ac0为单向阀的有效过流面积/m2;sign()为符号函数，定义为:

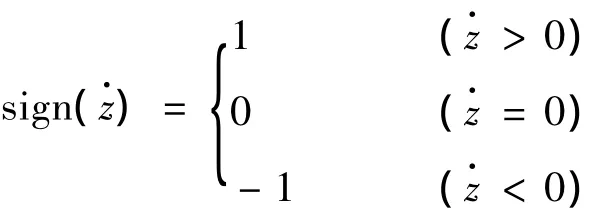
式中:p4为蓄能器内的压力/Pa;μ为油液的动力粘度/(Pa·s);dp为连接蓄能器和主油室的液压软管的内径/m;lp为连接蓄能器和主油室的液压软管的长度/m;V3、V4为副气室、蓄能器气囊内气体的体积/m3;V3s、V4s为静平衡位置时副气室、蓄能器气囊内的气体体积/m3;r为气体多变指数。

式(1)～式(8)所示即为该结构类型的油气弹簧的数学模型，当对活塞—活塞杆组件施加外部激励信号时，即可通过该方程组得出悬架缸的输出力F。

1.2 油气悬架系统1/2车辆模型的数学模型的建立

图2为基于该结构类型油气弹簧的某军用越野车悬架系统四自由度1/2车辆模型的振动模型。

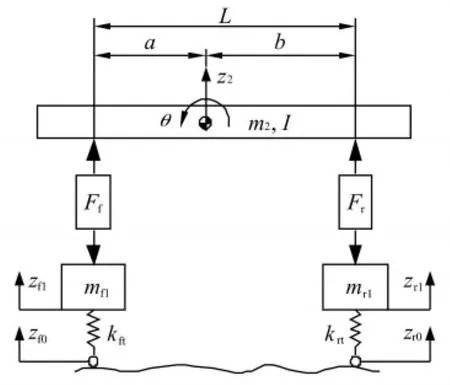
图2 油气悬架系统1/2车辆振动模型Fig.2 Half-car model of hydro-pneumatic suspension system

以静平衡位置为坐标原点，应用牛顿第二定律可以得到其动力学方程如式(9)～式(12)所示。

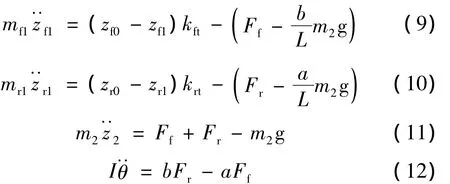
式中:mf1、mr1为前、后轴非簧载质量/kg;Ff、Fr为前、后油气弹簧的输出力/N;kft、krt为前、后轮轮胎刚度/N/m;zf0、zr0为前、后轮的路面位移激励/m;zf1、zr1为前、后非簧载质量的位移/m;m2为簧载质量/kg;z2为簧载质量质心的位移/m;I为簧载质量的转动惯量/(kg·m2);θ为簧载质量的俯仰角位移/rad;L为轴距/m;a、b为前、后轴到簧载质量质心的距离/m;g为重力加速度/(m·s－2)。

由于前后油气弹簧的悬架缸与簧载质量铰接，因此前后悬架缸的位移zf2和zr2可分别用式(z2－aθ)和式(z2+bθ)来表示。于是，前后油气弹簧的输出力Ff和可以分别用和代替式(2)中的，由式(1)～式(8)计算得到。

2 油气弹簧优化设计问题的描述

以上建立了油气弹簧的单缸数学模型和油气悬架系统四自由度1/2车辆模型的数学模型，基于此，应用Matlab/Simulink可以建立该1/2车辆模型的仿真模型，通过构建路面谱，可以仿真得到该1/2车辆模型的悬架系统的性能。对油气弹簧进行优化设计，是通过一定的算法不断改变油气弹簧的主要参数，然后对其仿真模型进行仿真，进而评价仿真输出的悬架系统的性能。当车辆悬架系统的性能达到要求时，即说明当前油气弹簧的参数是符合要求的。优化设计过程的示意图如图3所示。

由优化设计工作的主要内容［4］知，首先要将设计问题的物理模型转变为数学模型，即确定设计问题的目标函数、设计变量和约束条件。以下详细讨论建立某军用越野车1/2车辆模型的前、后油气弹簧的优化设计数学模型。

2.1 目标函数的确定

通常对悬架进行优化设计时，选用的目标函数为平顺性、悬架动行程和轮胎接地性，即常用的评价悬架系统性能的三个指标。最常用的是采用平顺性作为单一目标进行优化设计，同时也可以将这三个指标的加权和作为目标函数，以寻求悬架系统综合性能的最优。

对于越野车来说，为了保证乘坐的舒适性和行驶的安全性，必须使平顺性和轮胎接地性达到要求。另外，由于越野车经常在较差路面甚至是无路的情况下行驶，其悬架动行程相对较大，一味地追求动行程的最小是没必要的，而且会对平顺性的最优化造成不利影响，因此这里通过约束条件来对悬架动行程进行处理，保证其满足要求即可。

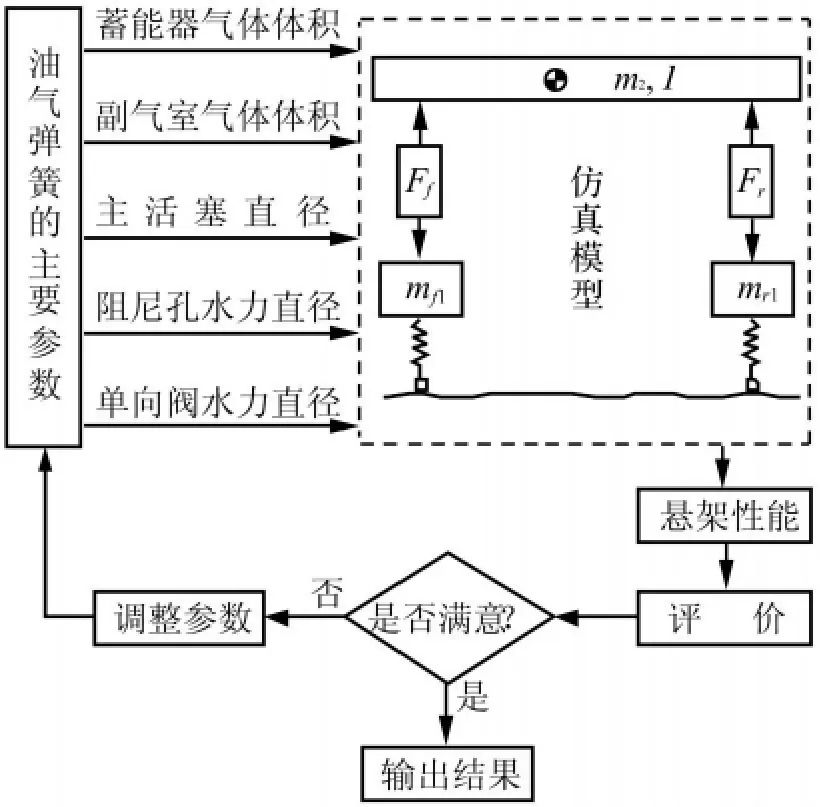
图3 油气弹簧优化设计过程Fig.3 Optimal design process of hydro-pneumatic spring

2.1.1 平顺性

对于1/2车辆模型来说，平顺性应该包括簧载质量的质心垂直振动加速度和俯仰角振动加速度。

(1) 质心垂直振动加速度

以质心垂直振动加速度表示平顺性时，可以采用簧载质量质心加速度均方根值［5～7］来评价，为了更加准确地对悬架系统的平顺性进行评价，本文采用ISO2631－1:1997(E)标准［8］所规定的平顺性的评价指标，即加权加速均方根值来表示，即:

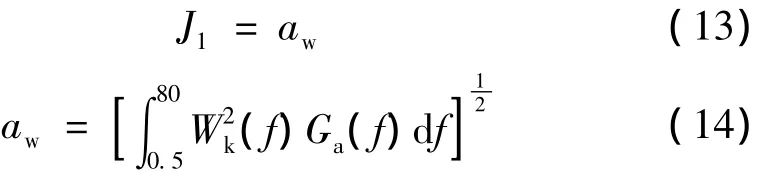
式中:J1为垂直振动加速度平顺性的目标函数;aw为簧载质量质心垂直振动的加权加速度均方根值，m/s2;f为频率，Hz;

Ga(f)为簧载质量质心垂直振动的加速度功率谱密度，m2·s－3;Wk(f)为垂直振动频率加权函数［8］，定义为:

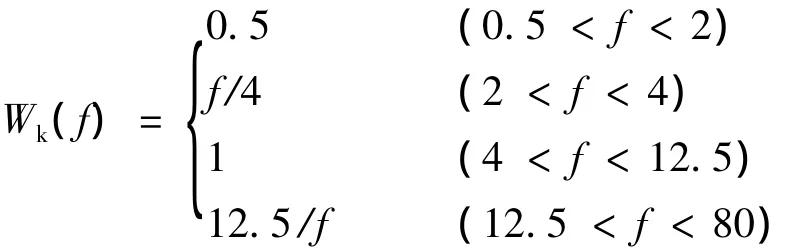
(2)俯仰角振动加速度

以俯仰角振动加速度来表示平顺性时，采用簧载质量俯仰角振动的加权加速均方根值［8］来表示，即:

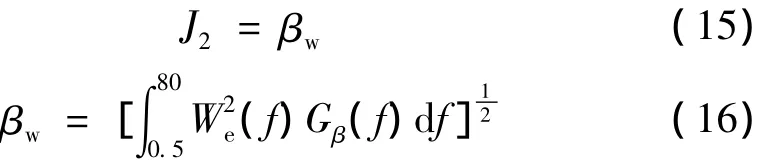
式中:J2为俯仰角振动加速度平顺性的目标函数;βw为簧载质量俯仰角振动的加权加速度均方根值/rad/s2;Gβ(f)为簧载质量角振动的加速度功率谱密度/rad2·s－3;We(f)为俯仰角振动频率加权函数［8］，定义为:

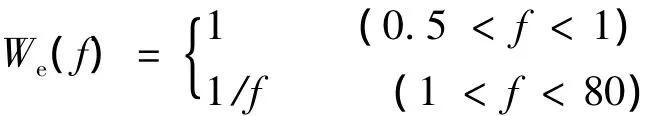
为了达到较好的乘坐舒适性，平顺性的目标函数J1和J2应尽可能小。

2.1.2 轮胎接地性

Sun［5］、Yoshimura et al［6］和 Hac［7］研究的关于轮胎接地性的目标函数采用非簧载质量和路面之间的相对位移的均方值 E［(z1－z0)2］来表示，本文采用车轮动载荷系数［8］来表示，如式(17)～式(19)所示:

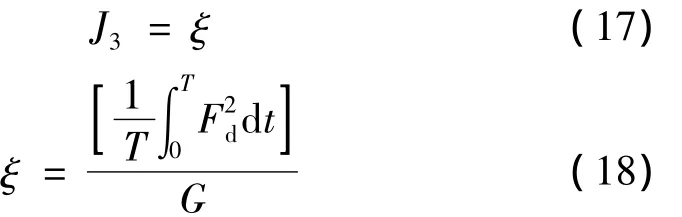
式中:J3为轮胎接地性的目标函数;ξ为车轮动载荷系数;Fd为车轮动载荷/N;kt为轮胎的刚度/(N·m－1);z0为路面位移激励/m;z1为非簧载质量的位移/m;G为车轮静载荷/N。

出于行驶安全角度的考虑，车轮动载荷系数也要尽可能小，以降低车轮与地面间脱离接触的可能性。

2.2 设计变量的选取

油气弹簧的主要参数均对油气悬架系统的工作性能产生影响［2］，而且其他的一些次要参数对悬架系统性能同样也存在着不同程度的影响［3］。因此，理论上应该把所有影响悬架系统性能的参数作为设计变量，通过优化设计过程进行确定。但实际中是不可行的，这样会使问题过于复杂、庞大，给求解带来困难，甚至导致求解失败。为了突出重点，这里仅确定对油气悬架系统特性影响程度较大的关键参数作为设计变量，包括前、后油气弹簧的主活塞直径、阻尼孔水力直径、单向阀水力直径以及平衡位置时副气室和蓄能器内气体体积与压力。

2.3 约束条件确定

对于一个优化设计问题来说，目标函数的数值取决于设计变量的数值。在实际问题中，为保证优化设计结果的可行性和合理性，设计变量的取值范围需要有一定的限制或必须满足一定的条件。油气弹簧的优化设计作为一个实际的工程问题同样也是受到很多条件的约束，具体分析如下:

(1)静平衡位置时的充气体积

对于静平衡位置时积蓄能器和副气室内的气体体积V4s和V3s，要根据油气弹簧的整体结构以及它们对悬架系统性能的影响程度来确定一个适当的范围，因此它们受到上下限的限制，即有:

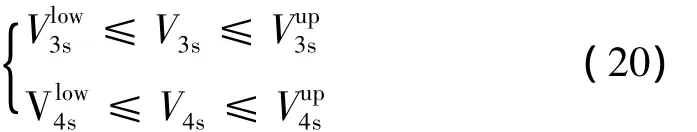
(2)主活塞直径和静平衡位置时气体压力

油气弹簧的优化设计是针对特定车辆在特定工况下的优化，而特定车辆特定工况下的质量参数是一定的。在静平衡位置时，油气弹簧内部的气体和液压油的压力是相等的，并作用于悬架缸来支撑簧载质量的重量。于是可得静平衡位置时主活塞直径d1和气体压力ps的关系为:

式(21)是一个等式约束，理论上，有一个等式约束就有从最优化过程中消去一个设计变量的机会［4］，因此用含d1的表达式来表示ps，并代入油气弹簧的数学模型中，从而可消去设计变量ps，使问题得以简化。d1和ps均存在上下限，而且彼此存在式(21)所确定的关系，因此，在综合考虑d1和ps的取值范围后，仅确定d1的取值范围即可，d1的取值范围为:

(3)阻尼孔和单向阀的水力直径

由文献［2］知，阻尼孔的水力直径Dd0对悬架系统性能的影响较单向阀的水力直径Dc0大。对于这两个参数，首先要依据其对悬架系统性能的影响确定一个适当的取值范围，即:

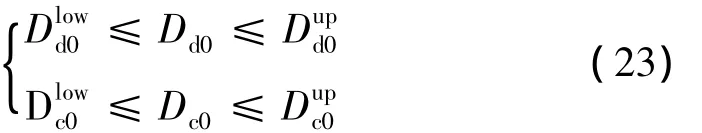
由图1所示的油气弹簧结构简图可以看出，阻尼孔和单向阀均开设在主活塞上，其详细的布置形式如图4所示。

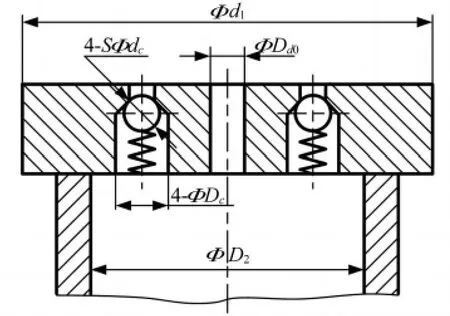
图4 阻尼孔和单向阀的布置形式Fig.4 Layout of damping hole and check valve

出于结构方面的考虑，需保证阻尼孔的直径与两个单向阀小孔的直径之和小于活塞杆中心空腔的直径，即有:

式中:Dc为单向阀小孔直径/m;D2为活塞杆中心空腔直径/m。

由流体力学知识可知，单向阀水力直径的表达式为:

式中:dc为单向阀球阀直径/m。

由于单向阀水力直径一般较小，仅有几个毫米，在适当选取一个单向阀球阀直径的情况下，单向阀小孔直径的变化不大，并且可由球阀直径和单向阀水力直径表示，则式(24)可变为:

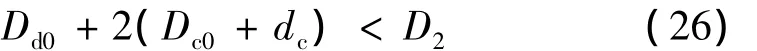
活塞杆中心空腔直径可以依据主活塞直径和活塞杆壁厚通过强度计算和结构设计得到，鉴于Dd0和Dc相对于主活塞直径小得多，一般有:

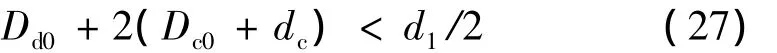
而通常D2＞d1/2，因此，Dd0和Dc0的约束关系可以由式(27)表示。

(4)簧载质量质心垂直振动的加权加速度均方根值

由文献［2］的研究可知，油气悬架系统的平顺性与其他两个性能是矛盾的，即平顺性的改善必然要导致悬架动行程和轮胎接地性的恶化，反之亦然，需要通过优化设计的方法来适当调整油气弹簧的参数以便在这对矛盾中寻求一种最佳的平衡。对于油气弹簧的多目标优化设计问题，首先要保证悬架系统的平顺性，优化设计的原则是在保证平顺性的前提下，使其综合性能达到最优。为此，需要对平顺性提出更为严格的要求，以免其为了给悬架动行程和轮胎接地性“让步”而过于恶化到不能接受的地步，即需使

由文献［8］知，当加权加速度均方根值aw＜0.315 m/s2时，人的主观感觉为“没有不舒适”，而当 aw=0.315 m/s2～0.63 m/s2时，人的主观感觉为“有一些不舒适”。考虑到车辆实际运行过程中不确定性因素的影响，这里对平顺性要求严格一些，取aw≤0.315 m/s2，以便当平顺性因不确定性因素的影响而变坏后仍能维持在可以接受的程度。

(5)悬架动行程

为了保证悬架动行程达到要求，需要对动行程的取值范围加以限定，以避免因限位块的撞击而引起悬架元件的损坏和舒适性的降低。对于越野车来说，其悬架动行程的实用范围［fd］［8］为7 cm ～13 cm。本文采用簧载质量和非簧载质量的相对位移的均方根值来衡量悬架动行程，即

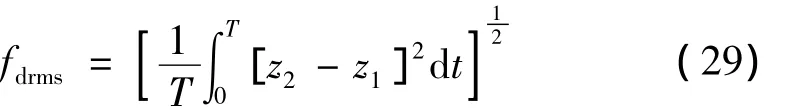
则fdrms的取值范围为:

式中:fdrms为悬架动行程的均方根值/m;为悬架动行程的上、下限/m。

2.4 油气弹簧优化设计的数学模型

以上分析了油气弹簧优化设计问题的目标函数、设计变量和约束条件。在约束条件限定的范围内，将各设计变量值的组合代入依据式(1)～式(12)所建立的油气悬架系统1/2车辆模型的仿真模型中，经过数据处理，即可得出各目标函数的值，并作为评价该组设计变量的依据。

综合以上分析，令前油气弹簧的设计变量为xf=［V3sf，V4sf，d1f，Dd0f，Dc0f］T，后油气弹簧的设计变量为xr=［V3sr，V4sr，d1r，Dd0r，Dc0r］T，即可得出 1/2 车辆模型的油气弹簧优化设计数学模型的标准形式如式(40)所示。需要说明的是，1/2车辆模型的油气弹簧优化设计数学模型中，平顺性目标函数J1和J2同时受到前后油气弹簧设计变量的影响，而目标函数J3则分别受到前后油气弹簧设计变量的影响。约束条件中，aw≤aupw同时影响前后油气弹簧设计变量的取值，而其余的约束条件则分别影响前后油气弹簧的设计变量取值。

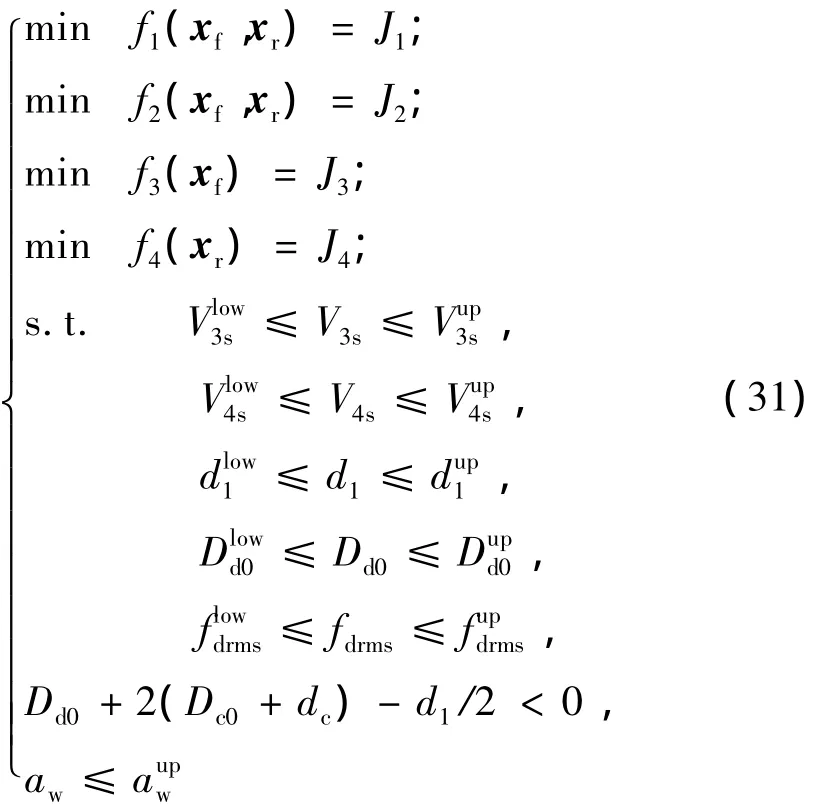
3 优化设计结果分析

由图3所示的油气弹簧优化设计过程可知，对于该多变量多目标非线性优化设计问题，传统的最优化算法是难以胜任的，只有群智能优化算法才可以处理。典型的群智能优化算法包括遗传算法、粒子群算法、蚁群算法、免疫算法、细菌觅食算法和Memetic算法等。本文采用粒子群算法进行求解。

表1 优化设计前后油气弹簧的主要参数Tab.1 Main parameters of hydro-pneumatic spring of non-optimal design and optimal design

应用固定权重和的方法处理优化设计的多目标问题，采用惩罚函数法处理后三个约束条件，并通过粒子的编码过程处理前五个关于设计变量的取值范围的约束。针对满载且以20 m/s车速行驶于B级路面的工况，应用粒子群算法，对以上所建立的基于1/2车辆模型的油气弹簧的优化设计模型进行求解。优化设计前后，前、后轴油气弹簧的主要参数如表1所示。优化设计前后，车身质心垂直振动加速度、车身俯仰角振动加速度和车轮动载荷曲线分别如图5～图8所示。

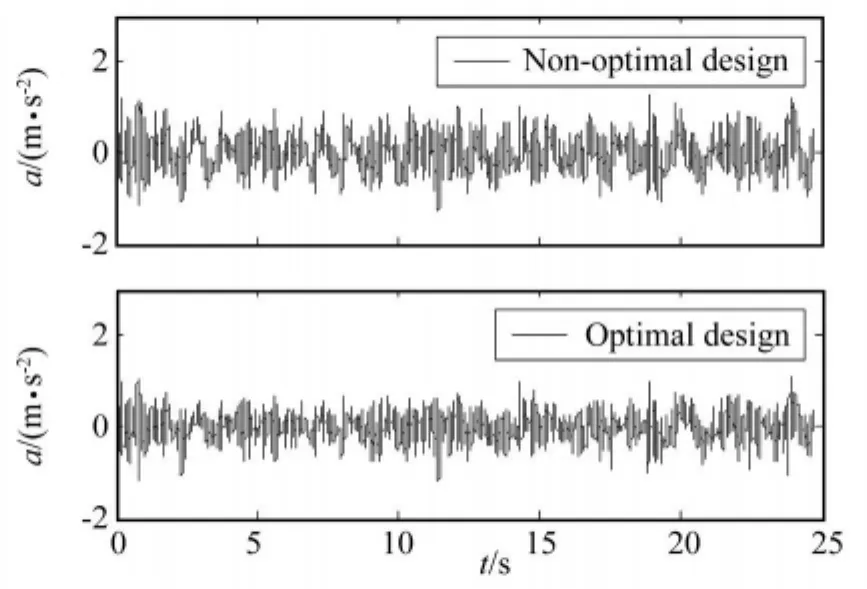
图5 车身质心垂直振动加速度Fig.5 Vertical vibration acceleration of barycentre of car body

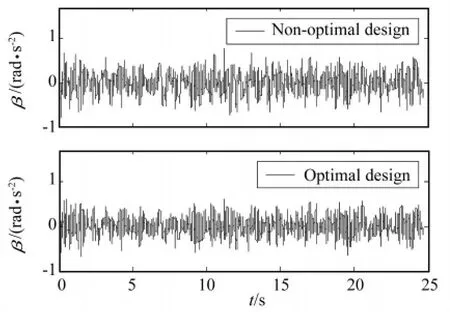
图6 车身俯仰角振动加速度Fig.6 Pitching angular vibration acceleration of barycentre of car body

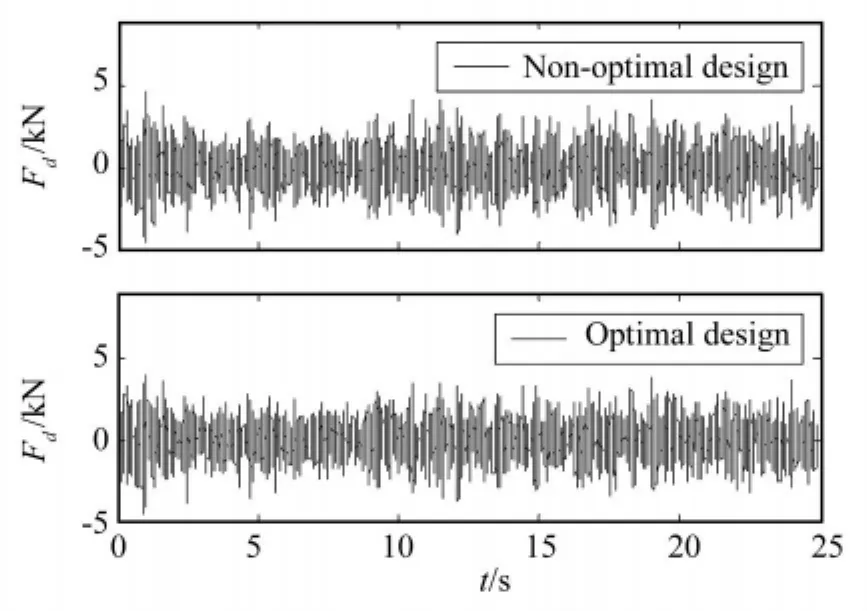
图7 前轴车轮动载荷Fig.7 Wheel ynamic load of the fore axis

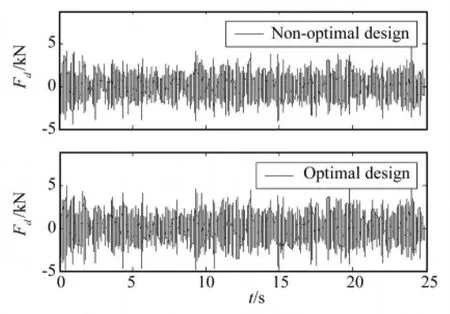
图8 后轴车轮动载荷Fig.8 Wheel ynamic load of the rear axis

对图5～图8所示的时域信号进行数据处理，得优化设计前后，悬架系统性能的对比情况如表2所示。

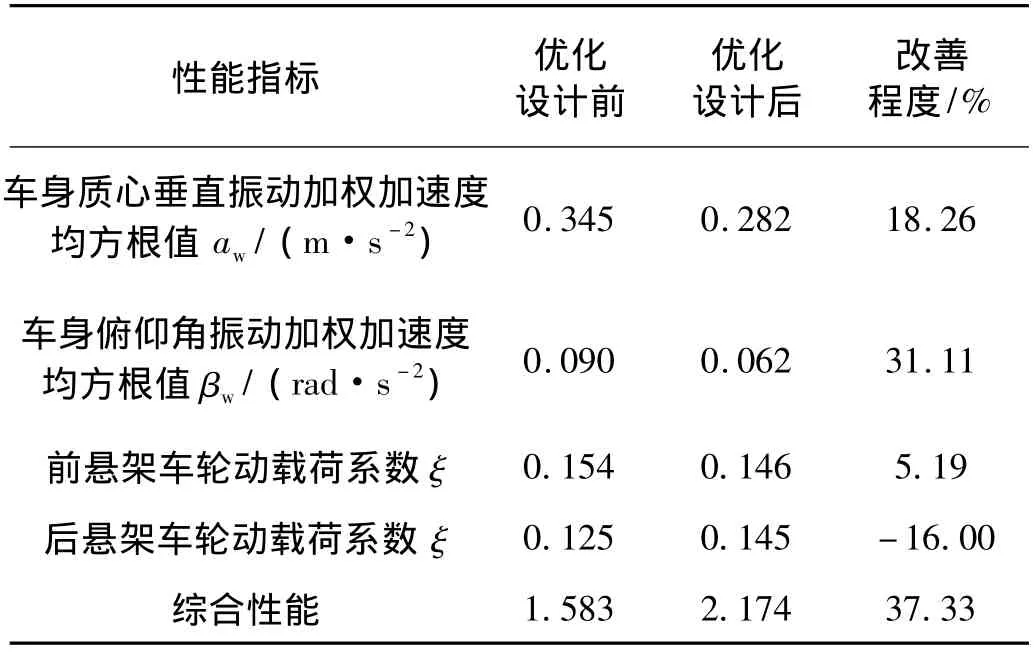
表2 优化设计前后悬架系统性能对比Tab.2 Comparison of the suspension performances between non-optimal design and optimal design

由表2的对比分析可知，车辆的平顺性得到了很大程度的提高，前悬架车轮动载荷系数也有了一定程度的降低，然而后悬架车轮动载荷系数却恶化了16.00%。究其原因，优化设计前，平顺性不太理想，而车轮动载荷系数却比较低，尤其是后悬架，悬架系统的性能严重的不匹配。通过优化设计，在允许的范围内增加了后悬架车轮动载荷系数，虽然“牺牲”了后悬架的轮胎接地性，但却为平顺性的改善做出了“贡献”，使悬架系统的综合性能，即悬架系统性能匹配的合理性得到大幅提高。

4 结论

本文详细讨论了油气弹簧的优化设计过程。问题的关键在于正确地建立油气弹簧优化设计数学模型，进而选用适当的最优化算法进行求解。本文是以某军用越野车为例来研究一种单气室油气弹簧的优化设计的，对于其他结构类型的油气弹簧，根据其所应用的车型，可以通过改变油气弹簧单缸数学模型、目标函数和约束条件来应用本文所阐述的方法进行优化设计，为最终形成一套简单易行、切实可靠的油气弹簧的设计方法奠定了基础。

［1］吴仁智.油气悬架系统动力学建模仿真和试验研究［D］.杭州:浙江大学，2000.

［2］仝军令，李 威，傅双玲.油气弹簧主要参数对悬架系统性能的影响分析［J］.系统仿真学报，2008，20(9):2271－2274.

［3］仝军令，李 威.非确定性参数对油气悬架系统性能的影响［J］.起重运输机械，2007(11):49－52，45.

［4］郁崇文，汪 军，王新厚.工程参数的最优化设计［M］.上海:东华大学出版社，2003.

［5］Sun L.Optimum design of“road-friendly”vehicle suspension systems subjected to rough pavement surfaces［J］.Applied Mathematical Modelling，2002，26(5):635－652.

［6］Yoshimura T，Edokoro K，Ananthanarayana N.An active suspension model for rail/vehicle systems with preview and stochastoic optimalcontrol［J］. JournalofSound and Vibration，1993，166(2):507－519.

［7］Hac A.Suspension optimization of a 2－DOF vehicle model using a stochastic optimal control techniques［J］.Journal of Sound and Vibration，1985，100(3):342－357.

［8］余志生.汽车理论［M］.第3版.北京:机械工业出版社，2000.