时变时滞和不确定模糊广义系统的鲁棒H∞控制

巩长忠，杨 敏

（中国民航大学理学院，天津 300300）

时变时滞和不确定模糊广义系统的鲁棒H∞控制

巩长忠，杨 敏

（中国民航大学理学院，天津 300300）

讨论了一类时变时滞参数不确定模糊广义系统的二次稳定性与鲁棒H∞控制问题。应用新的T-S模糊系统模型对其进行了描述，并给出了系统的二次稳定性定义。应用新的Lyapunov函数和线性矩阵不等式，给出了判定系统二次稳定的更为松弛的条件。一个H∞状态控制器确保了闭环系统具有H∞性能。最后的仿真实例验证了结论的有效性和可行性。

鲁棒H∞控制；模糊广义系统；时变时滞；参数不确定性；线性矩阵不等式

在实际工程中，许多非线性、不确定性、多变、时滞、有界干扰使得控制对象的精确数学模型难以建立，单一运用传统的控制理论和方法难以满足复杂控制系统的设计要求。而模糊控制则无需知道被控对象的精确数学模型就可以处理那些定义不完善或难以精确建模的复杂过程。

一个典型的模型就是T-S模糊模型，它是基于一系列if-then规则的基础之上，对一类不确定非线性系统进行模糊建模。随着研究的深入，这类描述方式被证明可以描述更广义的系统，同时对这类系统的鲁棒H∞控制也取得了让人欣慰的成果。文献[1-2]通过模糊Lyapunov函数及广义系统方法，对模糊控制系统的稳定性进行了研究，但没有讨论控制输入的延时。本文应用文献[3]的方法，引入新的控制器及Lyapunov函数，得到了新的判定条件，并在判定条件下，讨论了该类系统鲁棒H∞控制器的设计问题。

1 时变时滞与参数不确定模糊系统描述

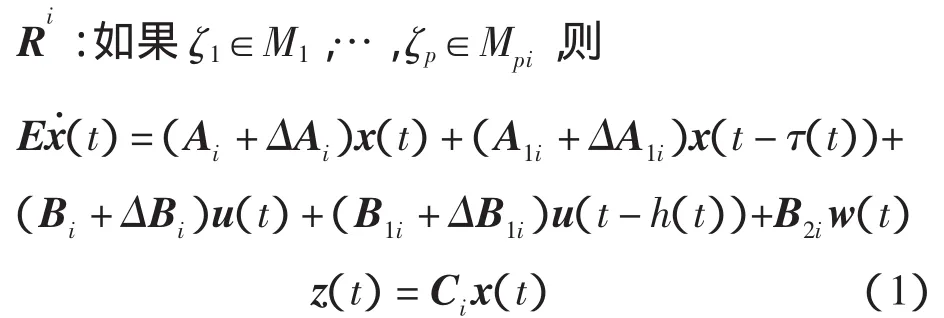
其中：Mij（i=1，2，…，r，j=1，2，…，n）是模糊集合；x（t）∈Rn是系统的状态空间向量；u（t）∈Rm是控制输入；w（t）∈Rm是外界扰动；z（t）∈Rl是被控输出；E∈Rn×n可以为奇异矩阵，通常假设 rank E=k≤n。τ（t）、h（t）是时变时滞函数，且存在正实数 τ0、h0、ρτ、ρh，使得对所有的时间t，满足

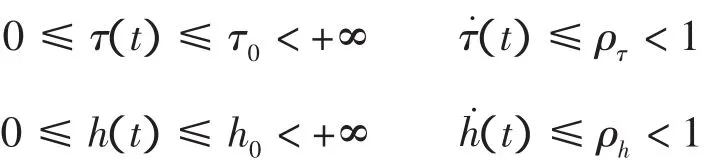
ζ1（t）、ζ2（t）、…、ζp（t）是前件变量。Ai、A1i、Bi、B1i、B2i、Ci是适当维数的实常数矩阵，ΔAi、ΔA1i、ΔBi、ΔB1i是系统中范数有界的时变参数不确定矩阵，可表示成如下形式

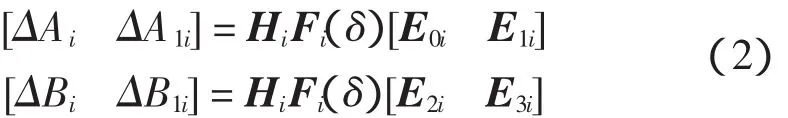
其中：Hi、E0i、E1i、E2i、E3i是适当维数的实常数矩阵；Fi（δ）是一个不确定的矩阵函数，满足Fi（δ）FTi（δ）≤ I。时变时滞参数不确定模糊广义系统的描述为

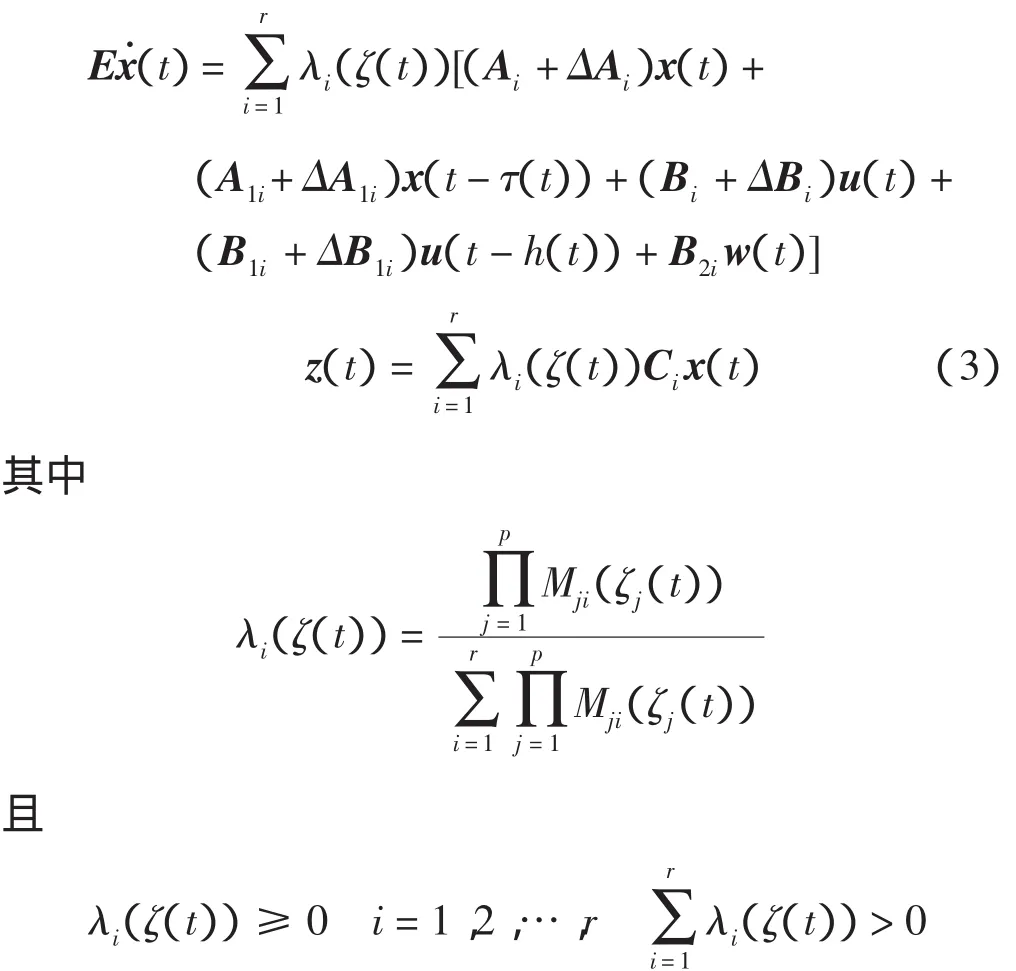
用λi、x、xτ、xh分别表示λi（ζ（t））、x（t）、x（t-τ（t））、x（t-h（t））。这时，系统（3）在没有控制输入与外界扰动时，可简记为

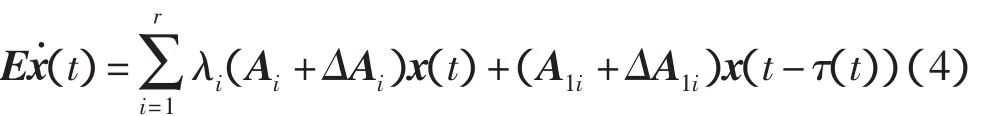
2 不确定模糊广义系统的鲁棒二次稳定性

定义1 模糊系统（4）是正则的，如果存在s∈C，使得[1]

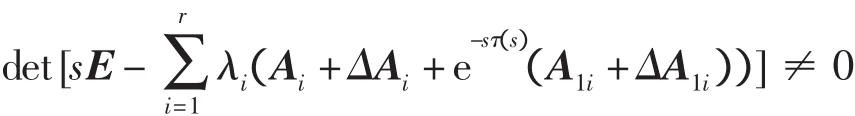
定义2 模糊系统（4）是无脉冲的，如果[1]

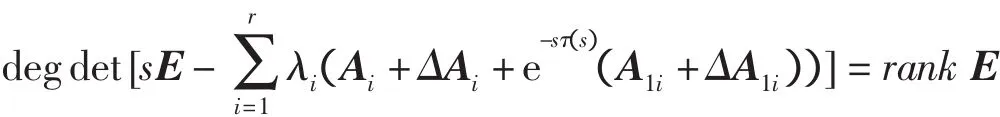
定义3 正则与无脉冲的系统（4）是鲁棒二次稳定的，如果满足[1]

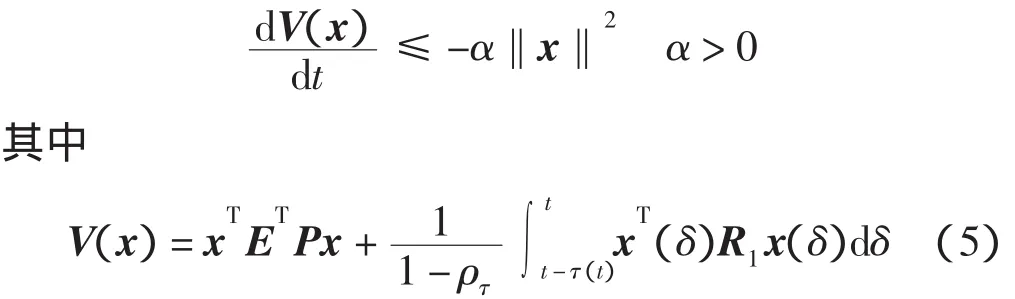
非奇异矩阵P满足P∈Rn×n，ETP=PTE≥0，R1是对称正定矩阵。

引理1 对具有适当维数的常数矩阵D，E及对称常数矩阵S，矩阵不等式

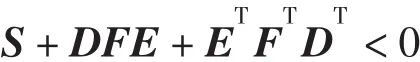
成立的充分必要条件是：存在ε>0满足下面的矩阵不等式

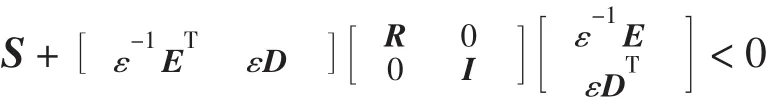
式中：F满足FTF≤R[4]。

将系统（2）代入系统（4），可以得到

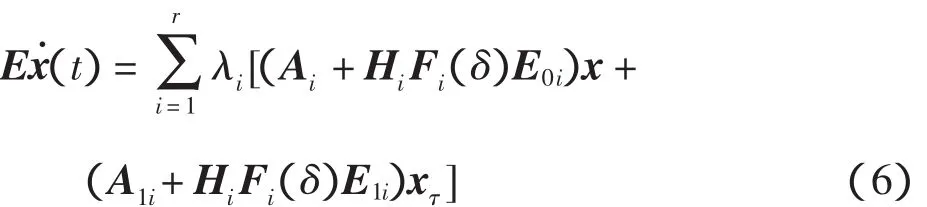
定理1 不确定模糊时变时滞系统（6）是鲁棒二次稳定的，如果存在非奇异矩阵R1>0，P和常量εi>0，i=1，2，…，r，满足

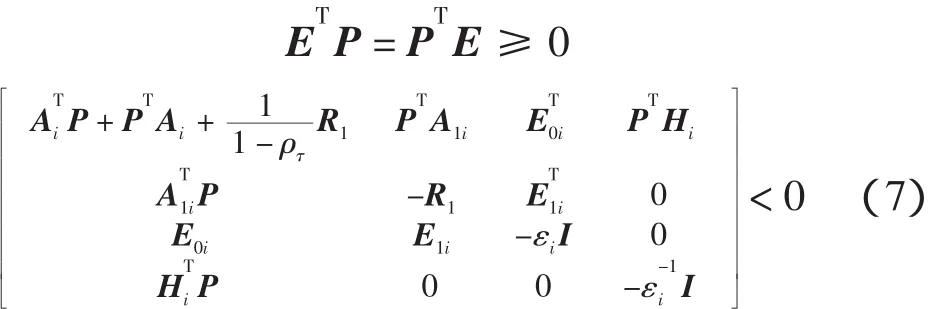
证明 取Lyapunov函数

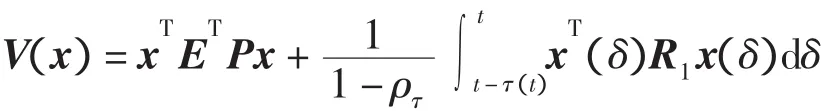
沿系统（5）的运动轨线是

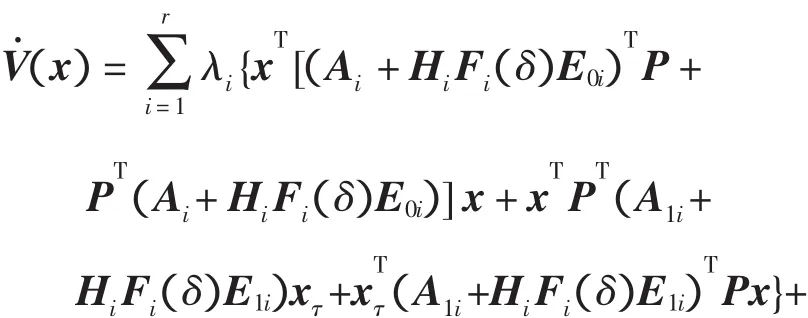
由引理1，上式等价于

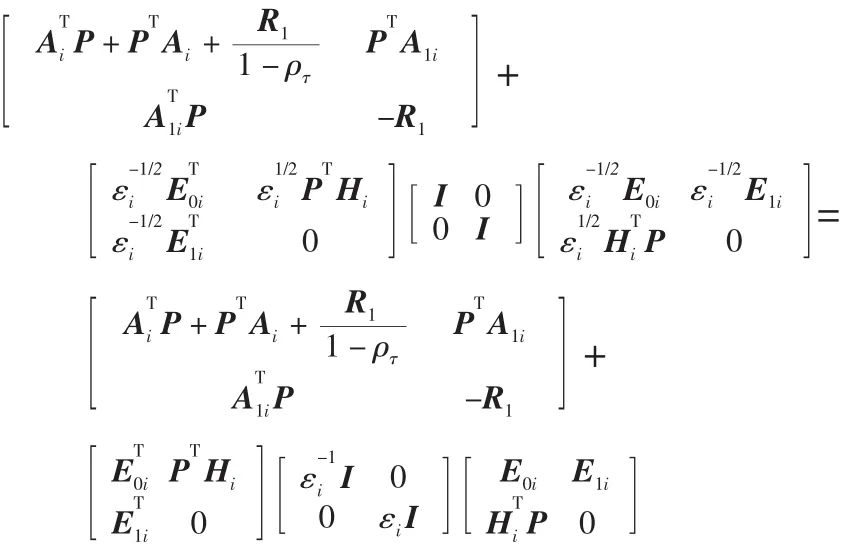
由定义3和schur补定理可知，上面矩阵

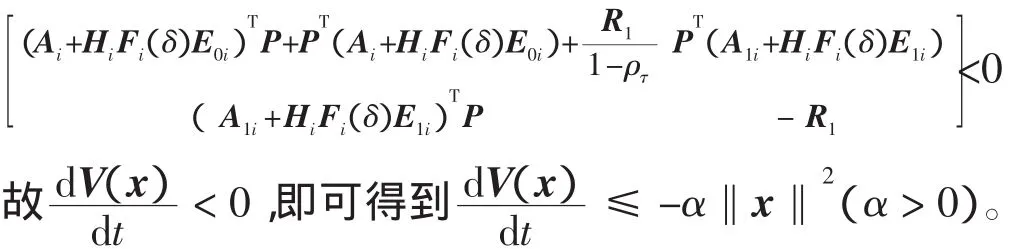
即系统（6）是鲁棒二次稳定的。

3 时变时滞参数不确定模糊系统鲁棒H∞控制

定义4 不确定时滞系统（1），在零初始条件下，若存在一个常数γ>0，使得对所有可接受的不确定性，使得‖z（t）‖2≤ γ‖w（t）‖，∀w（t）∈ L2[0，∞]，则说系统的H∞范数小于γ[1]。

定义5 对不确定模糊系统（3），如果存在一个模糊控制器，使得所得出的闭环系统是鲁棒二次稳定的，则系统（3）称为是二次能镇定的[5]。

对于 Ri：如果 ζ1∈M1，…，ζp∈Mpi，则 u（t）=Kix（t），i=1，…，r，则可得到全局模糊控制器为

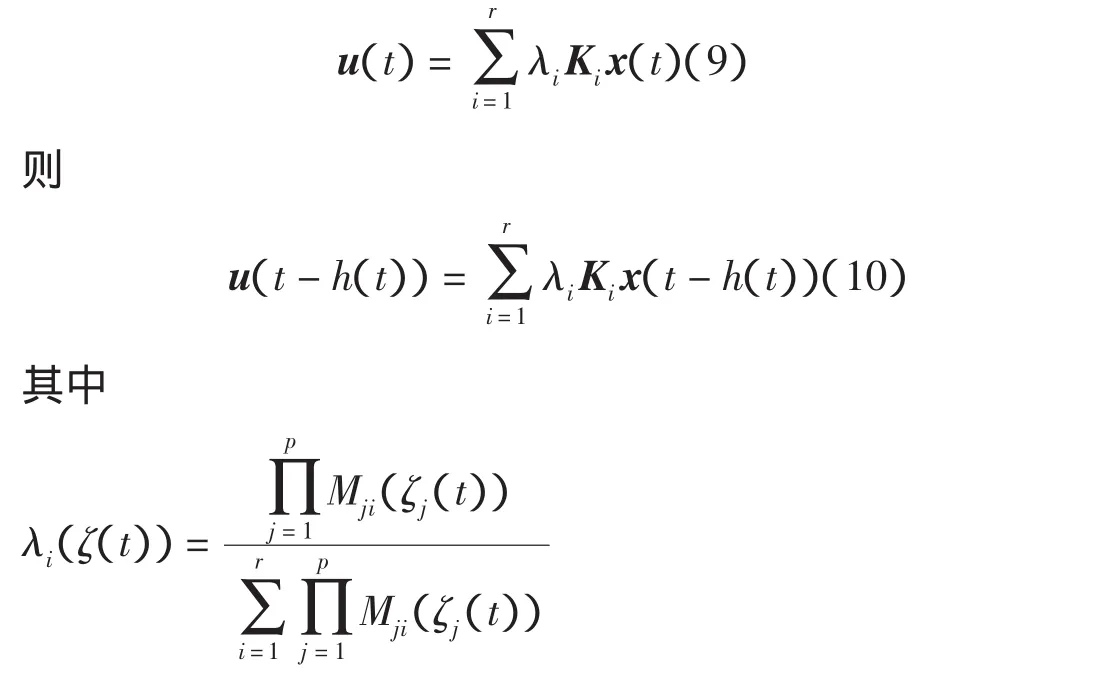
将系统（2）、系统（9）、系统（10）代入系统（3），可得到闭环系统

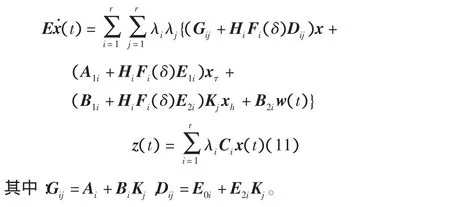
定义6 正则与无脉冲的系统（11）是鲁棒二次稳定的，如果满足[1]

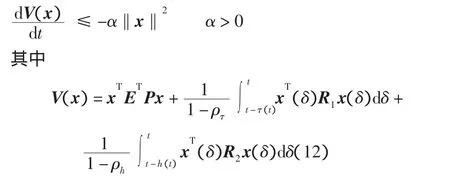
定理2 时变时滞系统（11）是鲁棒二次可镇定的，对任意 w（t）≠ 0，w（t）∈L2[0，∞），且满足鲁棒 H∞

范数约束条件‖z（t）‖2≤γ‖w（t）‖2。若下列条件式（12）～式（16）满足

*表示对称部分的转置。

证明 取Lyapunov函数

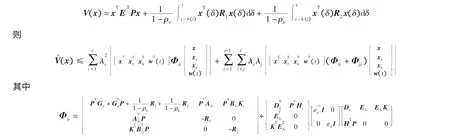
由schur补引理，等价于

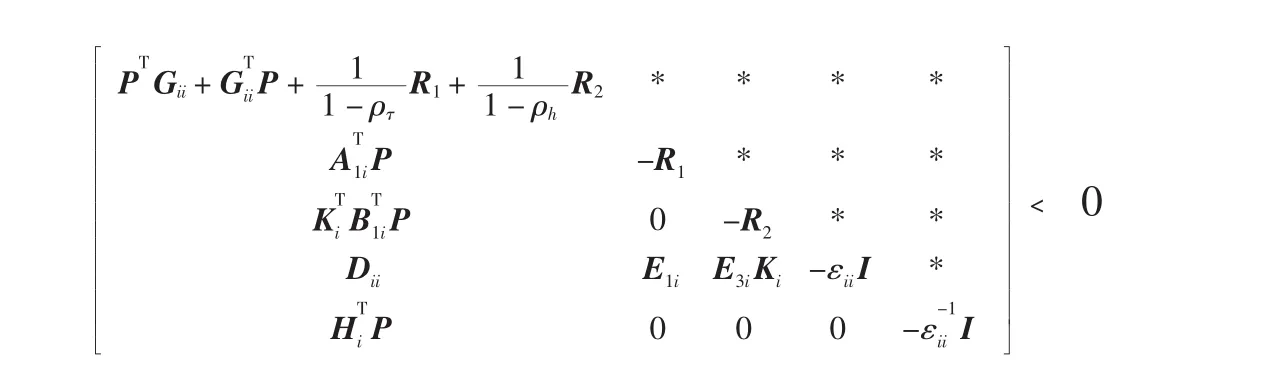
上式左右分别乘

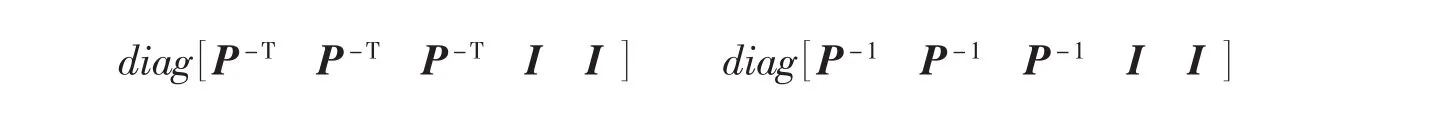
可得式（14）

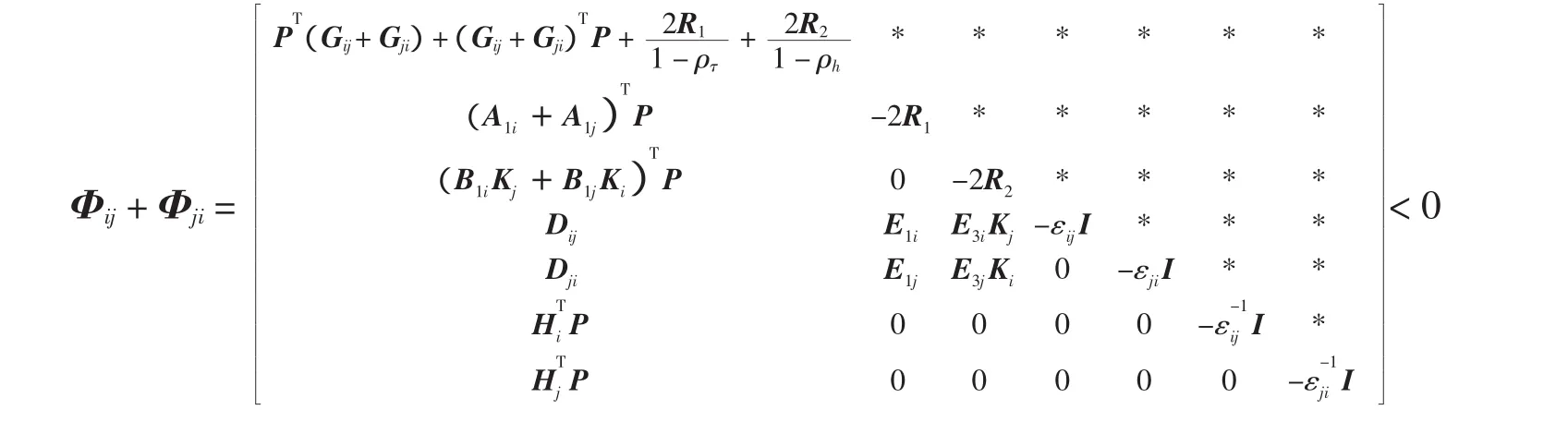
左右分别乘

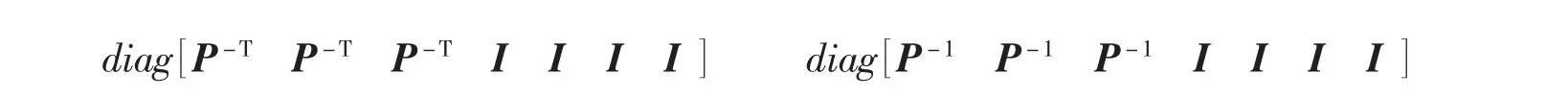
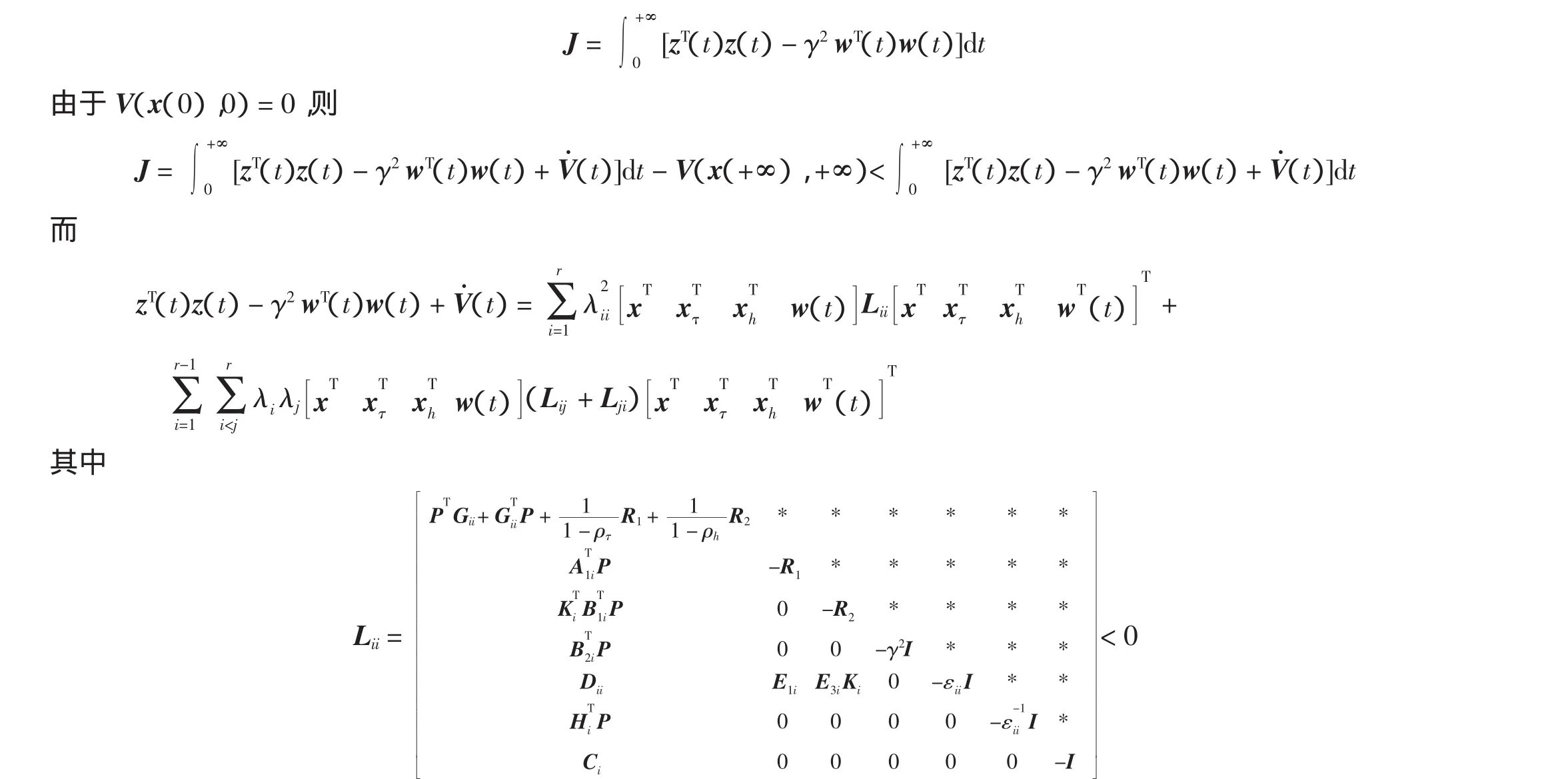
上式左右分别乘

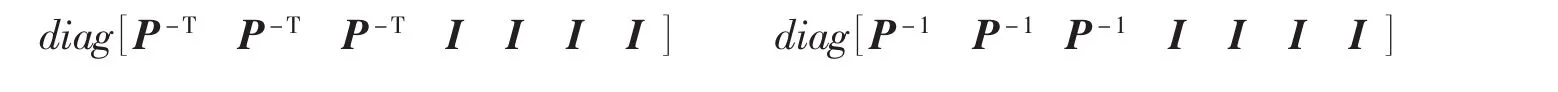
可得式（16）。

同样的方法，Lij+Lji＜0等价于式（17）。由式（16）、式（17），原系统具有 H∞性能。

4 仿真实例

假设如下模糊系统：

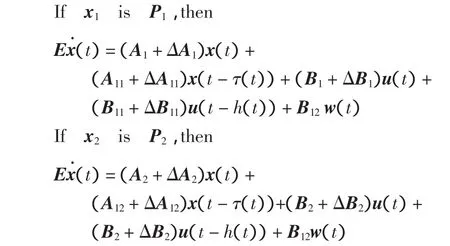
其中P1、P2的隶属函数分别为

应用 Matlab LMI Control Toolbox解式（12）～式（16），可得到

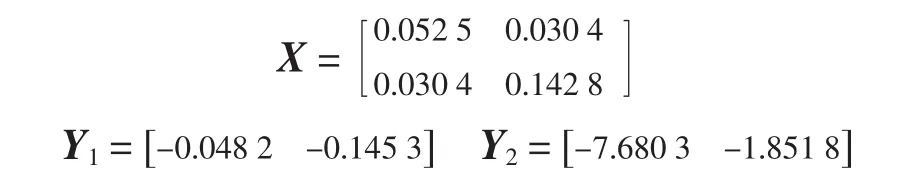
则两个状态反馈增益

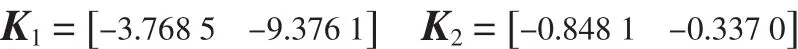
则系统具有鲁棒二次稳定性，且具有鲁棒H∞范数有界性。

γ=0.5时，鲁棒模糊控制器为

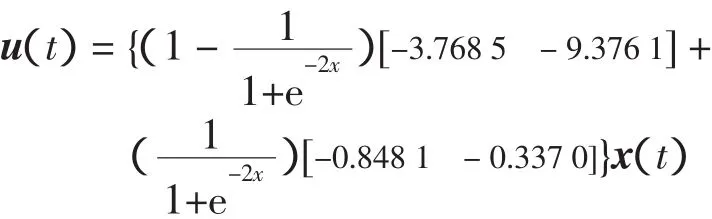
5 结语

本文讨论了时变时滞与参数不确定模糊广义系统的鲁棒二次稳定性与鲁棒H∞控制问题，对输入的时滞参数不确定性，用LMI方法，解决了稳定性问题。并通过设计模糊控制器，证明了范数有界不确定模糊广义系统具有的鲁棒H∞性能。

[1]TIAN WEIHUA，ZHANG HUANGUANG，YANG XIUMIN.Robust H∞Control for Fuzzy Descriptor Systems with Time－Varying Delay and Parament Uncertainties[C]//Third International Conference on Natural Computation，Haikou，August 24－27，2007：2－4.

[2] XU S Y，DOOREN P V，STEFAN R，et al.Robust stability and stabilization for singular systems with state delay and parameter uncertainty[J].IEEE Trans on Automatic Control，2002，47（7）：1122－1128.

[3] BAO－PING MA，JISUN.Robust Stabilization of Uncertain T－S Fuzzy Descriptor Systems[C]//Proceedings of the Third International Confer ence on Machine Learn ing and Cybernetics，Shanghai，August 26 －29，2004：334－337.

[4]佟绍成，王艳平，王 涛.基于状态观测器的一类非线性系统的模糊鲁棒控制[J].控制与决策，2001，16（1）：62－64.

[5] 苏宏业，褚 健，鲁仁全.不确定时滞系统的鲁棒控制理论[M].北京：科学出版社，2007：74.

Robust H∞Control for Fuzzy Systems with Time-Varying Delay and Parameter Uncertainties

GONG Chang-zhong，YANG Min
（College of Science， CAUC， Tianjin 300300， China）

The problem of robust quadratic stability and robust H∞control for a class of fuzzy descriptor systems with time-varying delay and parameter uncertainties.A new T-S fuzzy descriptor systems model with disturbance is proposed and the quadratic stability for the system is introduced.A more relaxed sufficient condition for the solvabiility of this problem is presented in terms of linear matrix inequalities （LMI） with a new lyapunov function.A state feedback H∞controller is determined to ensure the closed system is quadratically stable and guarantee the H∞performance.Finally，a numerical example is presented to demonstrate this method.

robust H∞control； fuzzy descriptor systems； time-varying delay； parameter uncertainties； LMI

PT202

A

1674－5590（2011）01－0036－05

2010-07-12；

2010-11-23

巩长忠（1959—），男，山东蓬莱人，教授，博士，研究方向为非线性控制与模糊控制.

（责任编辑：杨媛媛）