屏蔽电缆转移阻抗时域测量方法研究
张 琦 石立华 周颖慧 邵志学
(解放军理工大学工程兵工程学院,江苏 南京 210007)
1. 引 言
屏蔽电缆广泛应用在各类场合。由于屏蔽结构、屏蔽材质的不同,在屏蔽效能上也存在着较大差异。反映电缆屏蔽层屏蔽效能本质的是电缆特征参数转移阻抗,以往对电缆屏蔽效能的评价主要通过转移阻抗的测量来实现。目前,对屏蔽电缆表面转移阻抗的测量方法主要有线注入法[1-2]和三同轴法[3-6]两大类。国内外已有不少学者对其进行试验与理论上的研究[7]。国内标准GB9023-1988[8]和国际标准IEC62153-4-3-2002[9]、EN50289-1-6-2002[10]给出了转移阻抗的明确定义,如图1所示。
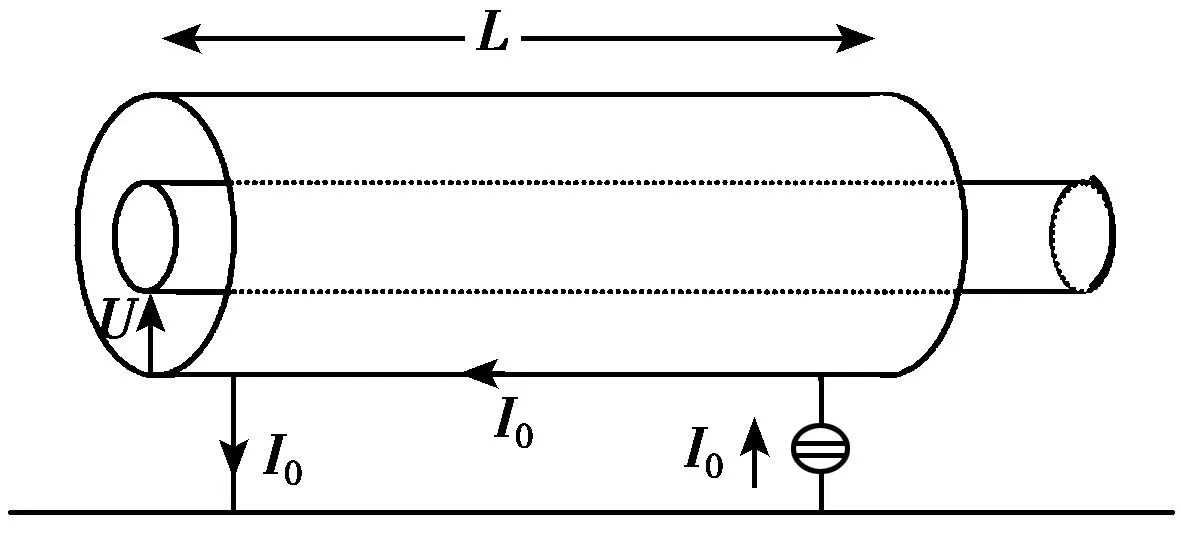
图1 转移阻抗的定义
转移阻抗的定义形式为
(1)
式中:I0是电缆屏蔽层上流过的电流; dU/dz是电缆屏蔽层与电缆芯线所组成的传输线上单位长度的电压降;I是电缆芯线上流过的电流。
以往转移阻抗的测量主要是在频域内进行的,即用网络分析仪对屏蔽电缆S参数进行测量,换算得到ZT(ω)曲线。而在一些场合需要直接评价电缆对电磁脉冲的屏蔽效果,频域测试曲线不能直观反映这一效果。周启明等人曾采用电磁脉冲直接注入的方法,测量了某多芯屏蔽电缆的屏蔽效果[11]。但是时域测量屏蔽效能与频域测量的互换方法,以往尚未有讨论。
本文针对屏蔽电缆表面转移阻抗时域测试需求,提出具体的实现方法,建立了时域测试系统;并与频域测试结果进行对比;研究了测试数据的建模方法,建立了转移阻抗的时域描述模型,为屏蔽电缆的屏蔽性能表征提供了新的参数模型。
2. 转移阻抗时域测试系统
2.1 测试系统设置
依据转移阻抗的测试标准,转移阻抗测试系统主要由高压脉冲源、三同轴装置、阻抗匹配网络、数字存储示波器、同轴衰减器以及受试件电缆等组成,测试系统构成如图2所示。图2中,三同轴测试装置适应频率范围为30 MHz以下时,样品长度为1 m;适应频率范围为100 MHz以下时,样品长度为0.3 m.如果最高测试频率为fmax(Hz),则允许的最大耦合长度[3]Lc,max为
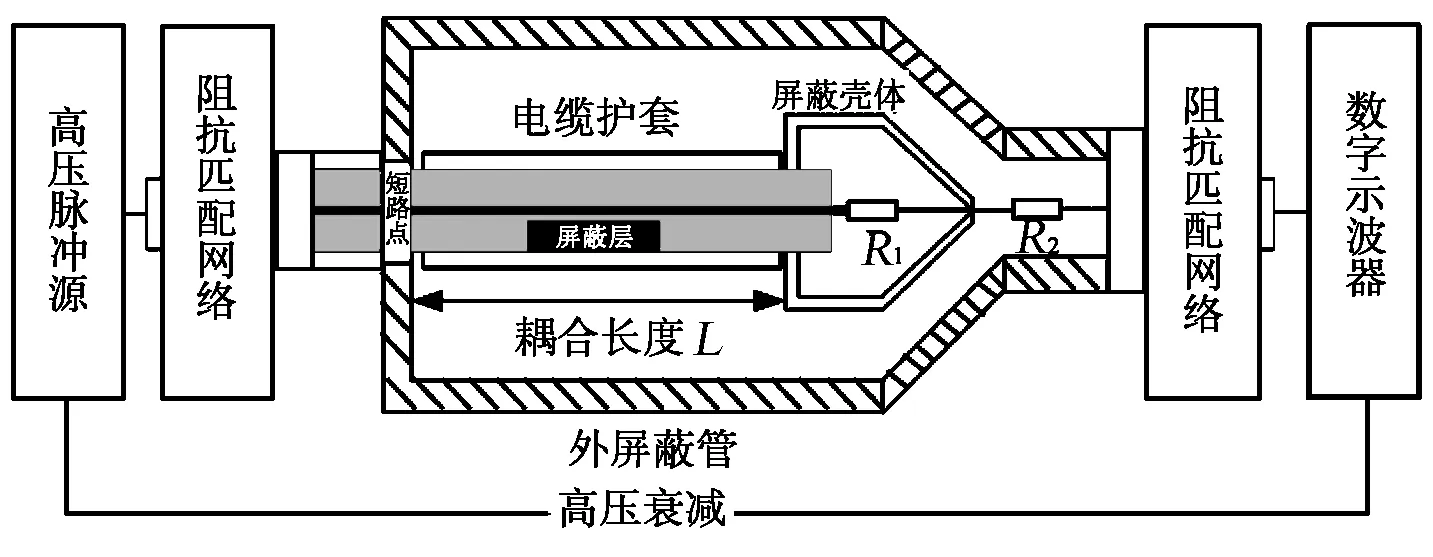
图2 转移阻抗时域测试系统图
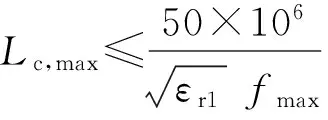
(2)
式中,εr1为电缆相对介电常数。
该测试系统中三同轴装置有效耦合长度为0.3 m,实际长度为0.45 m,屏蔽套管外径为51 mm,内径为48 mm,管厚为3 mm.其测试原理为:高压脉冲源注入信号至三同轴测量系统的内电路,数字存储示波器同步监测外电路耦合的电压信号。同时,示波器同步接收了高压脉冲源注入的源信号。测试系统实际将电流注入至屏蔽电缆芯线,测量屏蔽电缆屏蔽层的耦合电压。由此可以从示波器得到注入内电路的电流波形数据和外电路耦合的电压波形数据,进而评价表面转移阻抗。
2.2 高压脉冲源选择
高压脉冲源作为屏蔽电缆转移阻抗测试系统的信号源设备,其输出波形的性能直接影响着测试系统的测量精度。测试系统能够测试不同屏蔽效能的电缆,要求测量信号具有较大的电压输出动态范围,考虑到示波器的最小接收电压为2 mV,脉冲源输出电压峰值至少应为200 V;同时,转移阻抗作为描述屏蔽电缆效能的本征参数,要求注入信号具有较宽的频谱。
本文采用的高压脉冲源[12]输出双指数脉冲波0~6 kV可调,上升沿时间2~3 ns,半宽度25 ns,输出阻抗50 Ω,具有同步10倍衰减输出端口,并附加方波发生器功能。输出的双指数脉冲波和方波均达到美军标准MIL-STD-461E[13]的指标要求。输出的典型脉冲波形及其频谱如图3、图4所示。
2.3 匹配负载与网络

图3 高压脉冲源输出的典型脉冲波形
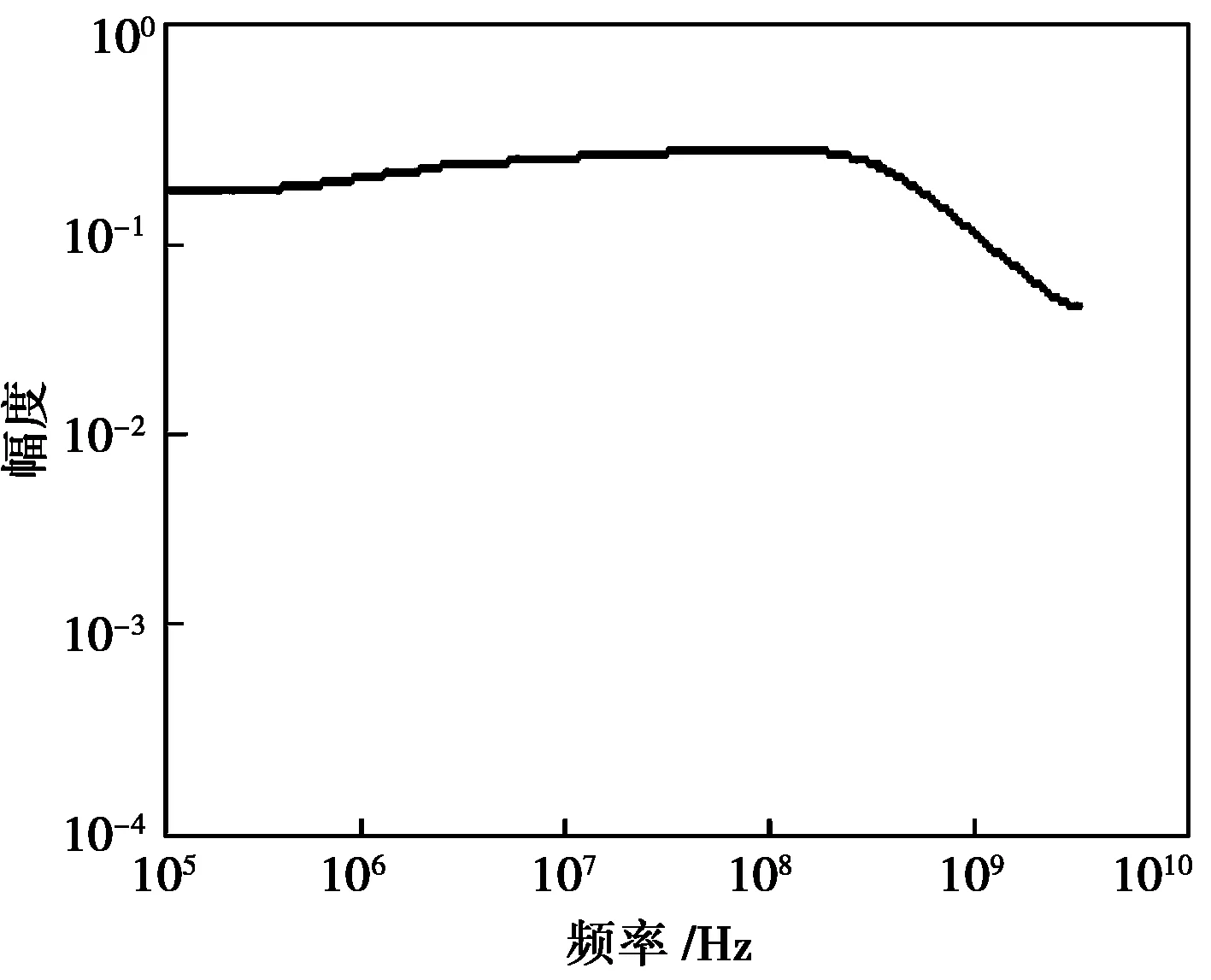
图4 高压脉冲源输出的典型脉冲波形频谱
测试系统内电路的输入和外电路的输出均要求匹配,达到50 Ω输入输出的标准。为保证负载匹配,图2中R1取值与内电路的特性阻抗Z1相等,R2取值与外电路的特性阻抗Z2相等。对于外屏蔽管取不同直径以及不同尺寸电缆的情况下,R2的取值可按以下两式计算[3]。
R2=1.4×Zout-50
(3)
(4)
式中:Dout为外层屏蔽铜管的内径,单位:mm;Din为电缆屏蔽层的外径,单位:mm.
内、外电路匹配负载的精确计算是非常重要的。内电路不匹配易形成反射,电流不能有效注入;外电路不匹配,测试系统得不到最大的耦合电压,均影响测量精度。如图2所示,该系统外电路的匹配负载设置在三同轴套筒的外面,可以更方便地调节负载大小,达到精确匹配的目的。当然,匹配负载设置在三同轴套筒外,必须要和匹配网络一样做好屏蔽,否则会影响测量精度。
以外电路匹配设计为例,若特性阻抗小于50 Ω,则匹配电路的连接方式如图5所示。图5中U2为外电路耦合电压,Uosc2为示波器测量值,R2为外电路匹配负载,RS、RP取值分别为
(5)
(6)
则匹配网络的增益系数为
(7)
若特性阻抗大于50 Ω,则匹配电路的连接方式如图6所示。图6中U2为外电路耦合电压,Uosc2为示波器测量值,R2为外电路匹配负载,RS、RP分别为
(8)
(9)
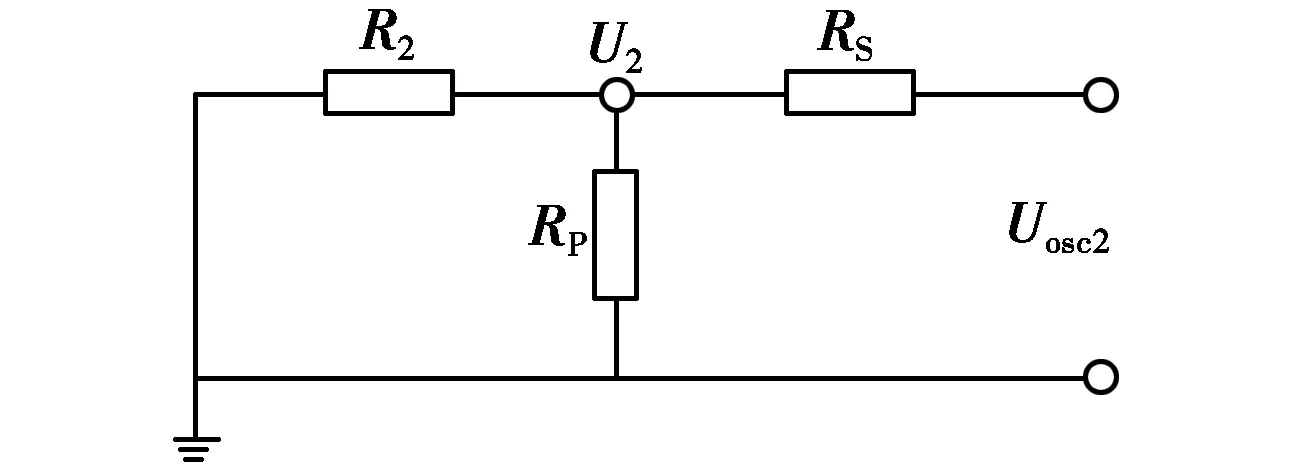
图5 特性阻抗小于50 Ω时的匹配电路
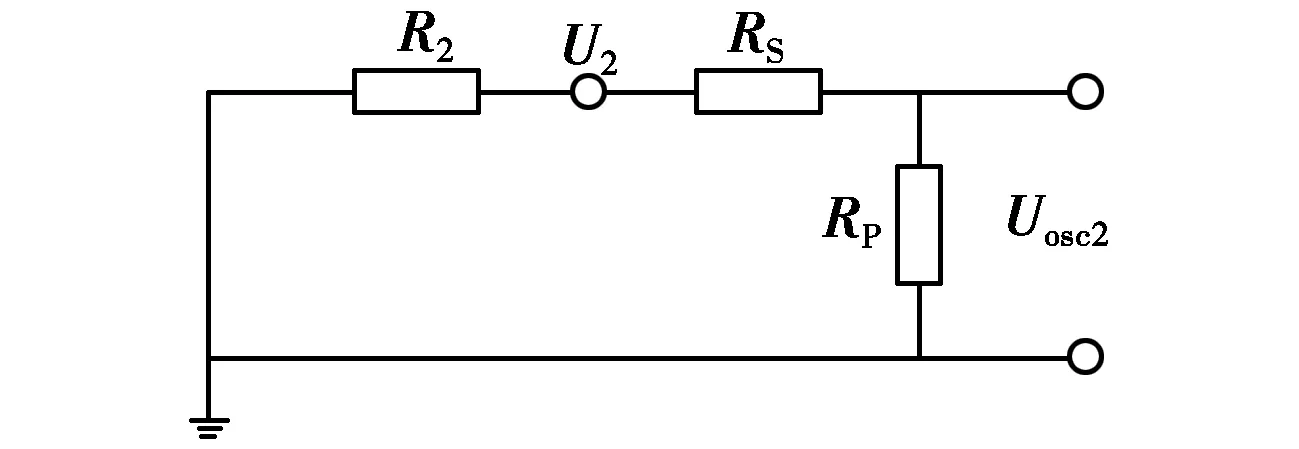
图6 特性阻抗大于50 Ω时的匹配电路
则匹配网络的增益系数为
(10)
由以上方法可以得到SYV-50-3型同轴电缆转移阻抗测试的相关数据为:R1=50 Ω,R2=183 Ω,RS=156 Ω,RP=59 Ω,K=0.5398。
测量系统采用LecroyWavRunner 6100A示波器作为信号接收机,其模拟带宽为1 GHz,最高采样速率为5 GHz,数据记录长度最高为1 M,可嵌入用户自定义数据处理功能。屏蔽电缆转移阻抗时域测试系统实物如图7所示。

图7 转移阻抗时域测试系统
3. 测试数据处理
测试得到系统注入电压Uosc1波形如图3所示,SYV-50-3型同轴电缆和SYV-50-5型同轴电缆耦合电压Uosc2波形,分别如图8、图9所示。
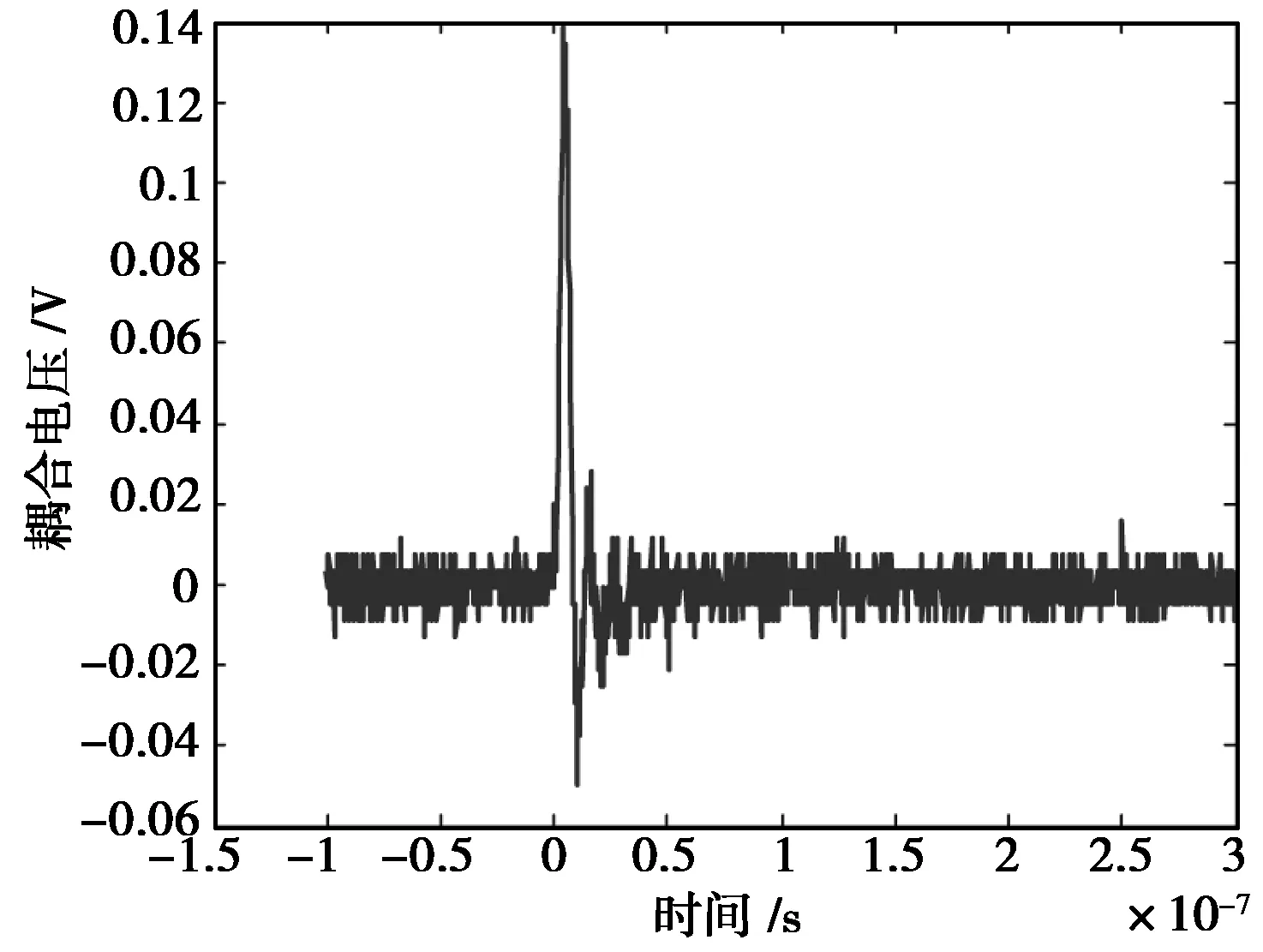
图8 SYV-50-3型同轴电缆耦合电压波形图
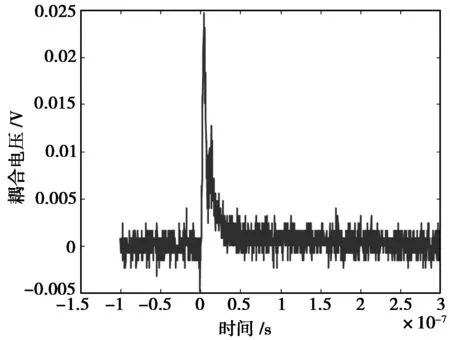
图9 SYV-50-5型同轴电缆耦合电压波形图
3.1 直接评价电缆的屏蔽效能
这是时域测试系统的一个最直接的应用。主要目的是评价特定长度的电缆对特定脉冲的屏蔽性能的好坏。首先,由示波器获取的数据计算注入电流I1和耦合电流I2,分别为
(11)
(12)
式中:M为高压衰减倍数,取值1000;K为匹配网络增益系数。
其次,计算电缆峰值屏蔽效能,计算公式为
(13)
式中:SEP为峰值屏蔽效能,单位:dB;I1,P为注入电流峰值;I2,P为耦合电流峰值。
以SYV-50-3型和SYV-50-5型同轴电缆为例,对图3所示双指数波脉冲峰值屏蔽效能分别为78.5980 dB和95.1380 dB.
同时,还可以观察电缆屏蔽效能曲线。分别对I1和I2做快速傅立叶变换,得到I1(jω)和I2(jω),则电缆屏蔽效能计算公式为
(14)
式中,SE为屏蔽效能,单位:dB.
SYV-50-3型和SYV-50-5型同轴电缆的屏蔽效能曲线如图10所示。
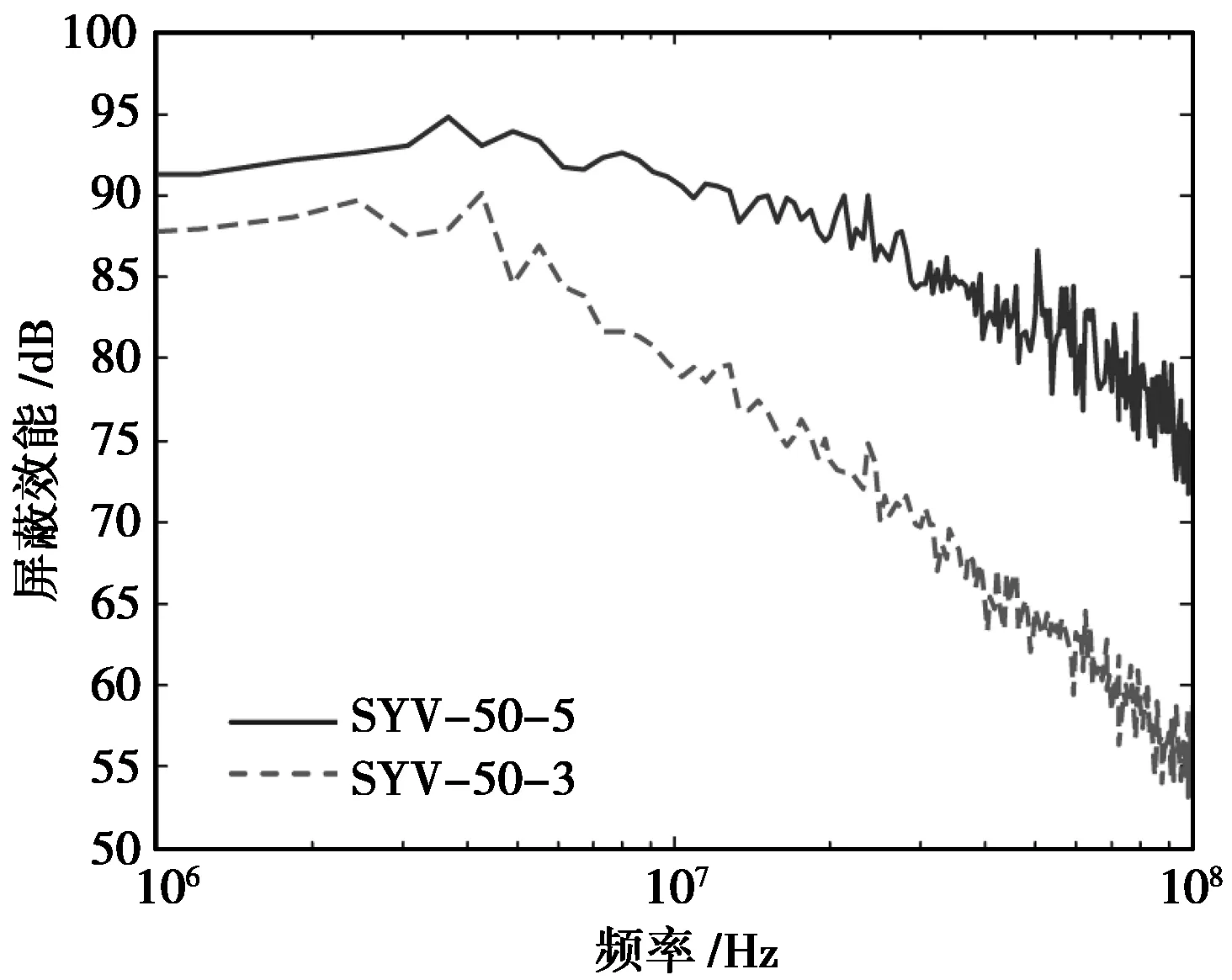
图10 同轴电缆屏蔽效能曲线
3.2 计算电缆转移阻抗ZT
由于转移阻抗是在频域下定义的,分别对I1和U2做快速傅立叶变换,得到I1(jω)和U2(jω)。则转移阻抗为
(15)
式中,L为有效耦合长度,取值0.3 m.
从而得到了转移阻抗曲线,如图11、图12所示。
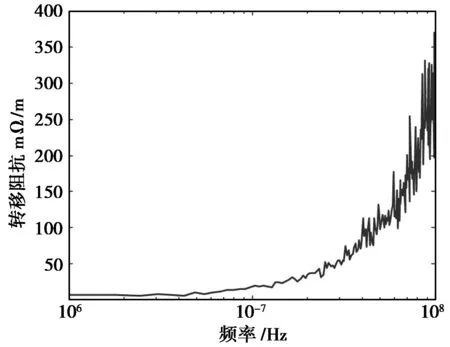
图11 SYV-50-3型同轴电缆转移阻抗
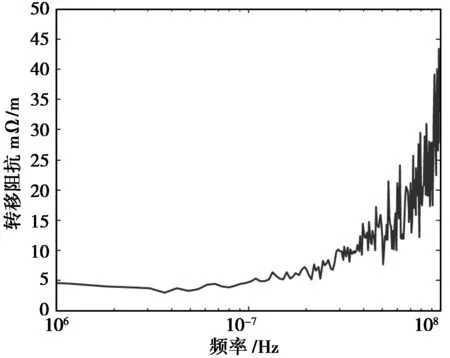
图12 SYV-50-5型同轴电缆转移阻抗
3.3 计算数据验证
为了验证时域测试系统的可靠性,使用Agilent 34401A多功能表直接测量电缆屏蔽层的直流阻抗,约在7~13 mΩ左右。此数据包含测量时的接触阻抗,具有一定的不确定性,但与转移阻抗时域测量曲线低频数据在同一数量级上,低频数据基本吻合。同时,使用Agilent 4396B网络分析仪进行频域测试,得到插入损耗
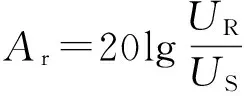
(16)
式中:Ar为插入损耗,单位dB;UR为网络分析仪耦合电压;US为网络分析仪注入电压。
将其转换为转移阻抗,计算公式为
(17)
式中:K为匹配网络增益系数;L为有效耦合长度。
从而得到频域测试下的转移阻抗曲线,与时域测试结果进行对比,两者基本吻合,如图13所示。
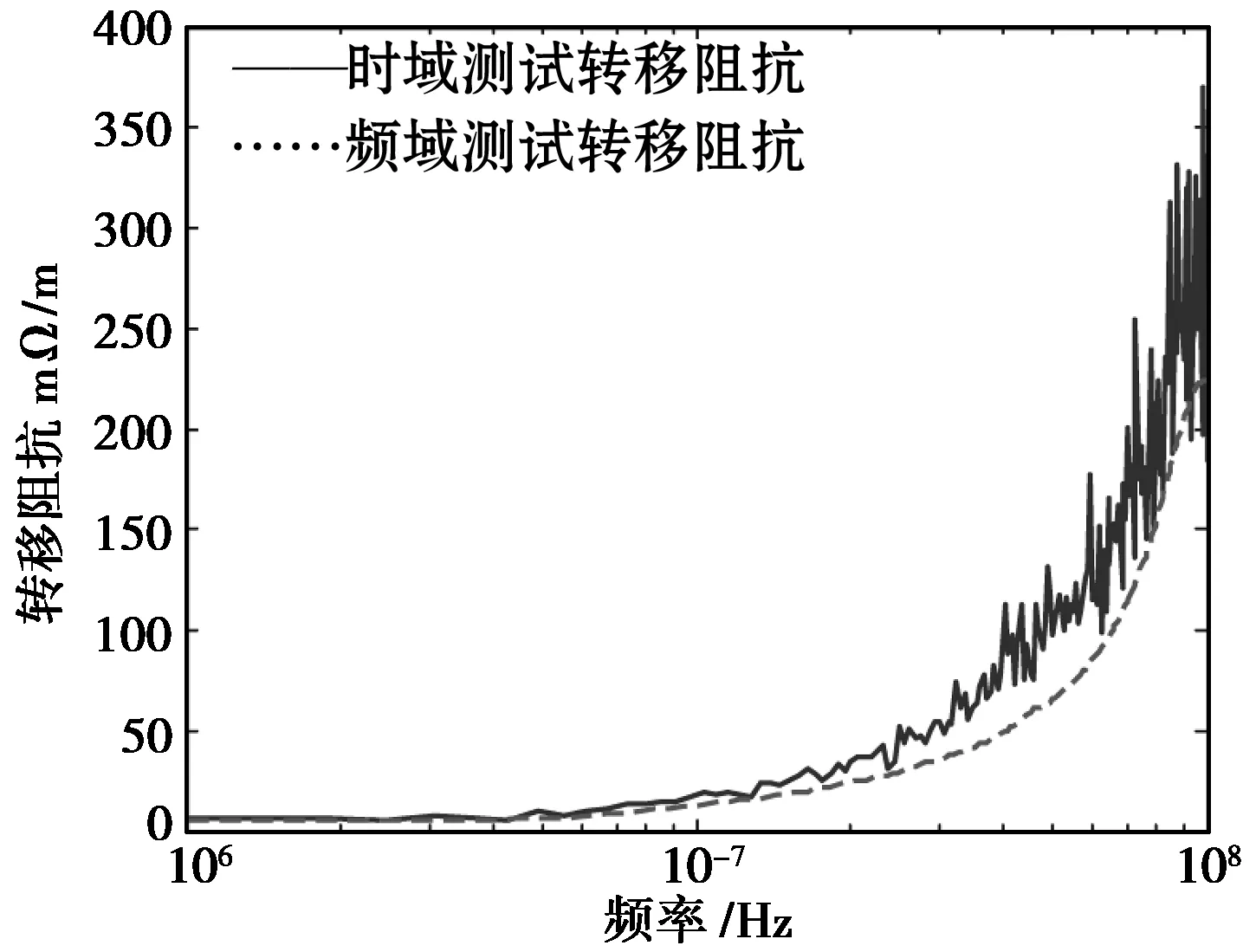
图13 SYV-50-3型同轴电缆转移阻抗时域与频域测试曲线
4. 转移阻抗参数化建模
图13中时域测试获得的表面转移阻抗曲线在高频段有较大噪声,是由于求取输入输出间传递函数时采用了式(15),在高频段信号受到噪声干扰,而除法运算放大了这一噪声,下面将讨论采用参数化模型去除这一影响。
4.1 选择参数化模型
由于屏蔽电缆是一个无源线性网络,转移阻抗可以作为一个线性系统的频率响应特性来分析[14-16]。根据信号与系统的基本原理,一个线性时不变(LTI)离散系统在时域中可以用线性常系数差分方程来表述为
(18)
由上式的Z变换得到
(19)
式中:H(z)为传递函数模型;M,N为模型阶数;a,b为模型参数;n,r,z-1为时间延迟。
因此,可以根据实测数据y(n)和x(n),为转移阻抗建立一个形式为式(19)的传递函数计算模型,该模型的参数化谱将有效抑制噪声的影响,同时便于在时域分析计算中应用[17]。
4.2 模型参数估计
参数估计要求使辨识出来的模型与实际的传递过程在某种意义上是最接近的。最小二乘法是一种在工程实践中应用最早和最广泛的基本方法,它依据的准则是模型输出与实际输出之间的误差平方和最小[18-19]。
考虑误差ε(n)的影响,将式(19)改写为
y(n)=-a1y(n-1)-…-aNy(n-N)+
b0u(n)+b1u(n-1)+…+
bMu(n-M)+ε(n)
(20)
针对输入数据时间序列为t=1,2,3,…,Nt的情况,写成矩阵形式
YN=HNθ+εN
(21)
式中:YN=[Y(1),Y(2),…,Y(Nt)]T
(22)
εN=[ε(1),ε(2),…,ε(Nt)]T
(23)
(24)
θ=[a1,a2,…,aN,b0,b1,…,bM]T
(25)
θ即为待估计的模型参数。根据参数估计的最小二乘法,设定目标误差函数为
(26)
则参数向量θ的最小二乘估计值为
(27)
以SYV-50-3型同轴电缆为例,它的参数化辨识结果如表1所示。

表1 SYV-50-3电缆转移阻抗模型参数辨识结果
则该屏蔽电缆转移阻抗传递函数为
(28)
图14(看824页)是利用式(28)对屏蔽电缆的电磁脉冲响应进行估计的结果,可见实际输出与建模输出十分相近,3阶模型可获得足够的建模精度。 模型参数化谱与时域测量转移阻抗曲线的对比效果如图15(看824页)所示。由此可见,参数化谱比较平滑,模型有效抑制了高频噪声。更为重要的是,式(28)形式的模型,简洁而完整地体现了屏蔽层表面转移阻抗的全部信息,与以往采用ZT(ω)曲线的表征方法相比,大大减少了数据量;同时,利用该模型估计屏蔽电缆芯线的响应,可直接采用式(19)形式的时域滤波算法,能够简化运算量。
4.3 模型有效性进一步验证
表1的模型参数是在前沿2.3 ns、半脉宽25 ns的双指数波条件下获得的。下面,将进一步验证该模型对其他输入波形响应估计的有效性。首先,采用前沿2 ns、脉宽100 ns的方波对SYV-50-3型同轴电缆进行测试,输入波形如图16所示。
采用表1的参数估计芯线耦合电压,并与实测输出波形对比,效果如图17(看824页)所示,两者的波形是吻合的。
此外,还对前沿5 ns、半脉宽100 ns的双指数波进行测试与估计,实测输出波形与建模估计波形也是吻合的。输入波形如图18所示,估计效果如图19(看824页)所示。
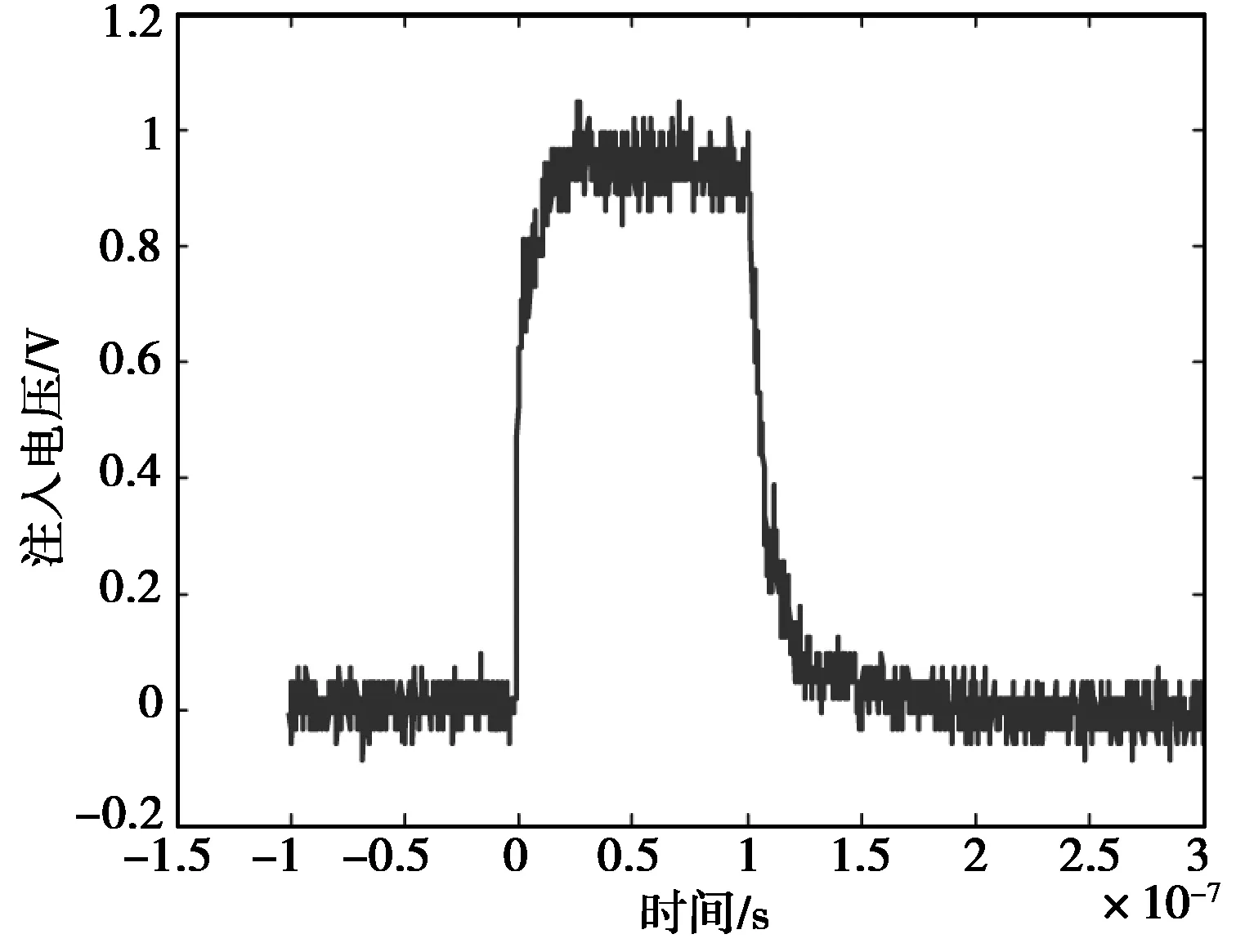
图16 输入的方波波形
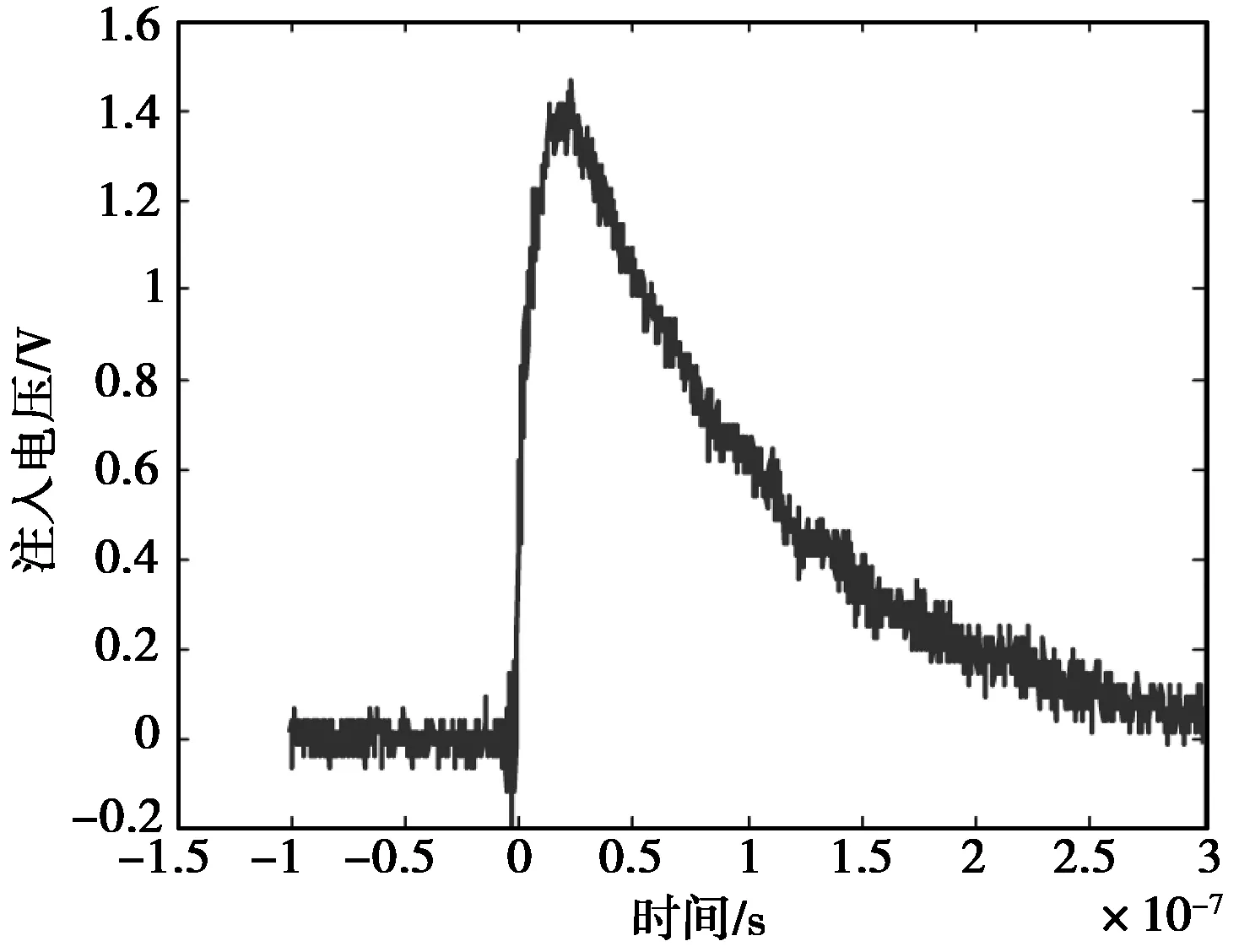
图18 输入的双指数波形
5. 结 论
本文提出了屏蔽电缆转移阻抗时域测试方法,建立了测试系统。时域测试不仅能够直观、形象反映电缆电磁脉冲的耦合情况,还能够换算获得表面转移阻抗曲线。在此基础上,提出了屏蔽电缆转移阻抗参数化建模方法,不仅可以获得更为清晰的转移阻抗曲线,更为重要的是,这一参数化模型是对ZT(ω)的一种更为简洁的表述,在场-线耦合分析中用于替代ZT(jω),将大大提高计算效率。
[1] LEE H Y, OH H S, PARK D C. Measurement of transfer impedance of shielded multiconductor telecommunication cables using IEC 96-1 line injection method[C]//Proceedings of the IEEE International Symposium on EMC, 2003, 3: 1012-1015.
[2] KOROVKIN N, NITSCH J, SCHEIBE H J. Improvement of cable transfer impedance measurement with the aid of the current line method[C]∥ Proceedings of the IEEE International Symposium on EMC, 2003: 1148-1151.
[3] 朱荣华, 李谦若. 表面转移阻抗的测量-三同轴方法[J]. 光纤与电缆及其应用技术, 2005, 39(4): 8-11.
ZHOU Ronghua, Li Qianruo. Measurement of surface transfer impedance-triaxial method[J]. Optical Fiber Electric Cable, 2005, 39(4): 8-11. (in Chinese)
[4] ORLANDI A. Frequency and time domain modeling of the transfer impedance and distributed longitudinal induced voltage by means of a spice equivalent circuit[J]. IEEE Trans. Electron. Comput., 2003, 45(1): 125-129.
[5] MORRIELLO A, BENSON T M, DUFFY A P, et al. Surface transfer impedance measurement: a comparison between current probe and pull-on braid methods for coaxial cables[J]. IEEE Trans. Electron. Comput., 1998, 40(1): 69-76.
[6] 雷 震, 蒋全兴. 基于遗传算法的转移阻抗测试装置优化设计[J] .电波科学学报, 2007, 22(1): 69-72.
LEI Zhen, JIANG Quanxing. Optimization design of transfer impedance testing device[J]. Chinese Journal of Radio Science, 2007, 22(1): 69-72. (in Chinese)
[7] 齐 磊, 崔 翔, 谷雪松. 屏蔽电缆转移阻抗和转移导纳的宽频测量[J] .电波科学学报, 2007, 22(4): 696-701.
QI Lei, CUI Xiang, GU Xuesong. Wide-frequency measurement of transfer impedance and transfer admittance of shielded cable[J]. Chinese Journal of Radio Science, 2007, 22(4): 696-701. (in Chinese)
[8] GB 9023. 射频同轴电缆屏蔽效率的测量方法(转移阻抗)[S]. 1988.
GB 9023. Methods of Measurement of Screening Efficiency for Radio Frequency Coaxial Cables-Test Method for Transfer Impedance[S]. 1988.
[9] IEC62153-4-3. Metallic Communication Cabletestmethods Part4-3: Electromagnetic Compatib-ility(EMC)Surfacetransfer Mpedancetriaxialmethod[S]. 2002.
[10] EN50289-1-6. Communication Cables Specification for Test Methods Part 1-6: Electrical Test Methods Electromagnetic Performance[S]. 2002.
[11] 周启明, 邓建红, 李小伟, 等. 脉冲电流注入法求多芯电缆的传输函数[J].信息与电子工程, 2006, 4(4): 254-257.
ZHOU Qiming, DENG Jianhong, LI Xiaowei, et al. Research of transfer function for multi-core cable by injecting method of current[J]. Information and Electronic Engineering, 2006, 4(4): 254-257. (in Chinese)
[12] 谭坚文, 石立华, 李炎新, 等. 快前沿高压脉冲源的开发及实验研究[J].强激光与粒子束, 2004, 16(11): 1434-1436.
TAN Jianwen, SHI Lihua, LI Yanxin, et al. Development and experimental research on the fast rise time EMP generator[J]. High Power Laser and Particle Beams, 2004, 16(11): 1434-1436. (in Chinese)
[13] MIL-STD-461E: Requirements for the Control of Electromagnetic Interference Characteristics of Subsystems and Equipment[S]. 1999.
[14] HANIQUE E. A transfer function is a reliable tool for comparison of ful-and chopped lightning impulse tests[J]. IEEE Transactions on Power Delivery, 1994, 9(3): 1261-1266.
[15]MALEWSKI R, POULIN B. Impulse testing of power transformers using the transfer function method[J]. IEEE Transactions on Power Delivery, 1988, 3(2): 476-489.
[16] 石立华, 周璧华. 自积分式脉冲磁场传感器的补偿研究[J]. 电波科学学报, 1995, 10(4): 50-55.
SHI Lihua, ZHOU Bihua. A compensation of the self integrating magnitic field sensor[J]. Chinese Journal of Radio Science, 1995, 10(4): 50-55. (in Chinese)
[17] ZHOU Yinghui, SHI Lihua, GAO Cheng, et al. Combination of FDTD with digital filter in analyzing the field-to-transmission line coupling[J]. IEEE Trans. on EMC, 2008, 50(4): 1003-1007.
[18] ORAIZI H. Application of the method of least squares to electromagnetic engineering problems[J]. IEEE Antennas and Propag., 2006, 48(1): 50-74.
[19] ORAIZI H. Solution of the junction of TE11-mode circular waveguides by the method of least squares[J]. International Journal of Engineering Sciences, 2004, 15(3): 25-39.

