对足球比赛中射门的博弈分析以及统计检验

张 啸

（武汉科技大学 管理学院，武汉 430081）

对于当今世界主流足球联赛的各个俱乐部来说，数据分析已经成为了非常常见同时也非常重要的一项工作.通过引入数学方法和统计学方法，球队的数据分析人员能够更加全面地了解足球比赛和球员，并归纳出比赛当中的一些不易被人直接观察得到的结论.

在足球比赛中，由于点球的特殊性，使其成为最容易引起学者关注的研究领域.例如，Chiappori[1]等人通过博弈论方法分析了球员在罚点球时的策略选择问题；Palacios-Huerta[2]同样也做过类似的分析.此外，其他一些学者也尝试过利用数学、统计学、物理学以及人类行为学等各种方法来分析罚点球时球员和守门员的策略以及行为特征.

本文将不把研究重点放在罚点球上，而是将比赛中一般情况下的射门作为考察对象.具体而言，将利用博弈论的方法建立一个数学模型，对一般情况下射门球员和守门员所处的状态进行模拟，并通过对模型的进一步分析，得到射门球员和守门员的策略选择倾向.在得出理论上的结论后，本文还将利用统计检验来验证这些结论.

1 建立数学模型

1.1 各种参数及假设

由于实际比赛中的策略选择以及行为之间的相互依赖关系非常复杂，在建立数学模型之前，我们需要对问题所涉及到的射门球员、守门员以及他们所面临的环境状态做出一些必要的规范化假设，这将有利于我们对问题的简化和分析.而这种简化并不会影响对问题核心内容的考察.

假设1：假定射门的球员在面临射门机会时，所处的位置并非正对球门.

这样假设的原因是：可以让球员面临两种区别更明显的选择，要么选择朝球门近角踢，要么朝球门远角踢.如果球员正好在中间位置，则可以预见到的是，球员在射门时会显得更随机化（在不考虑球员可能存在某些个人射门习惯的情况下），而守门员也不会去选择极端的站位（门柱附近）.

因此，在本模型中，射手在射门时面临的情况就是选择近角或者远角.

假设2：假定博弈过程是存在先后顺序的（虽然这种时间上的先后顺序可能并不明显），首先，对于门将来说，在球员射门前，他们会选择自己的站位；之后，对射门球员来说，他们会根据观察到的门将的站位情况来选择是射远角，还是射近角.

为了将门将的站位进行量化分析，我们把球门的长度设定为1，并令门将与球门远角之间的距离为p，p显然满足p∈[0，1]，因此，博弈的过程可以表示为图1.

图1 守门员和射门球员策略选择过程

而球员和守门员站位的示意图如图2所示.

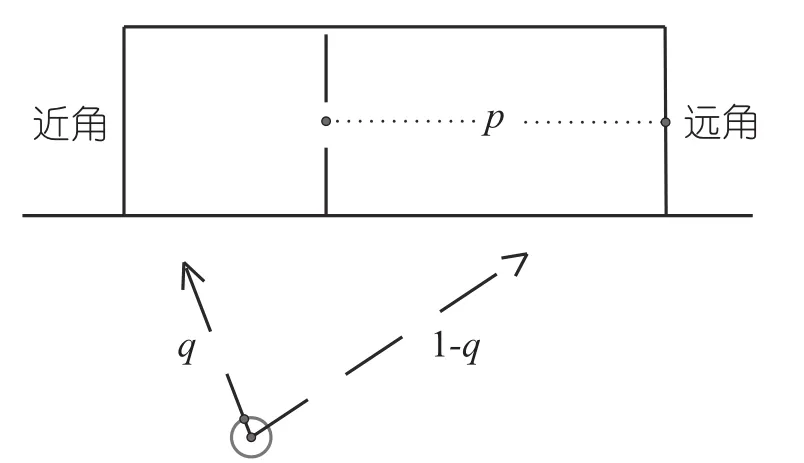
图2 守门员和射门球员站位选择

在图2中，上方的矩形表示球门，球门中间的虚线是对守门员的抽象，下方的圆形表示球员射门时的位置，从守门员到球门远门柱之间的距离设为p，从足球向两方延伸的箭头虚线表示射手可能选择的两个射门方向，即近角和远角，并且向近角射门的概率为q，向远角射门的概率为1-q.

假设3：射门的结果是随机的，也就是说，即使球完全按照射手的意愿被踢出，最终也不一定能打在射门球员所期望其到达的球门近角或者球门远角的球门范围之内.

为了量化这种假设，我们设想球员在选择射近角的时候，足球按照球员期望落在近角球门范围之内的概率为α，且α∈（0，1）；球员在选择射远角的时候，足球按照球员期望落在远角球门范围之内的概率为β，且β∈（0，1）.

假设4：假设3当中的α和β实际上是对射门精确程度的一种测度，为了简化问题，假设射门的精确程度与两个因素有关，一个是射手的技术，另一个是射手的射门位置.

为了表示出这两种影响因素，我们考虑为概率α和β建立两个函数表达式：令α=μhα（δ），β=μhβ（δ），其中，μ代表球员的技术水平对精度的影响，且我们令μ∈（0，1）；另一方面，hi（δ）代表射门位置对精度的影响，i=α，β，其中，δ是位置变量，并且为了简单化，我们同样规定δ∈（0，1）.可以看出，μ的变化将同等程度地影响到射远角和射近角时的射门精度.

假设5：在不考虑射手自身技术水平μ的情况下，射近角的精度要大于射远角的精度，即对于一切δ∈（0，1），都有hα（δ）＞hβ（δ）.这实际上是在假设4基础上的一个引申假设，这个假设也是符合现实情况的.

假设6：球能否踢进球门，除了与球能够按照球员的意愿命中球框范围之内相关之外，还取决于守门员是否能对来球做出及时准确的反应，以及门将的站位选择.令守门员的反应速度用参数ζ来表示，且令ζ∈（0，1）；而守门员的站位在前面已定义，用参数p来刻画.

假设7：在不失一般性的情况下，在分析时，我们将会忽略掉那些没有命中球门范围内的情况，也就是说，我们不会去考虑和区分那些射高了或者射偏了的射门，而只会考察那些射在球门范围内的情况.

1.2 得益情况分析

根据前面一节的假设和参数设定，我们希望可以得到射手的得益情况（注意，由于射门是一个零和游戏，所以这里实际上可以省略掉对守门员得益情况的分析），为此，我们设想得益情况用“射门精度”、“门将站位”以及“门将反应速度”这三个参数来表示.并且，得益与“射门精度”正相关，而与“门将站位”以及“门将反应速度”负相关.因此，我们可以得到射门球员在选择近角或者远角并且进球时的期望得益：

其中，（1-ζ）表示守门员没有能够及时做出反应.

容易看出，此问题不存在纯策略纳什均衡.原因在于，守门员在射手选择时，最好的选择是p=0，而在射手选择时，守门员最好的选择是p=1，所以不存在纯策略纳什均衡.但是，此问题存在混合策略纳什均衡.我们令射手选择近角的概率为q，选择远角的概率为1-q，则可以得到如表1表示的双方得益情况.

表1 守门员和射门球员得益情况

其中，逗号前面的式子表示射门球员的期望得益，逗号后面的式子表示守门员的期望得益.注意，此处的矩阵不是得益矩阵，而只是对射门球员和守门员的期望得益情况进行了一个表达.实际上，由于在这个博弈中守门员所面临的选择p是连续的，我们无法很好地通过得益矩阵来表示博弈双方的得益情况.

首先，对于守门员来说，要通过让p随机化，使得射手无论选择近角或者远角，最后的期望得益是无差异的.即守门员所选择的p需要使得下式成立：

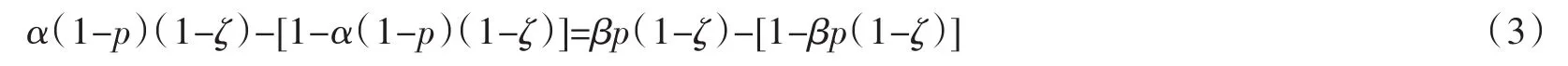
可以解得p的均衡值为：p=α/（β+α）.

其次，对于射手来说，要通过让射门选择概率q随机化，使得守门员无论选择任何p，最后的期望得益是无差异的.即射手所选择的q需要使得下式不会因为p的改变而改变：

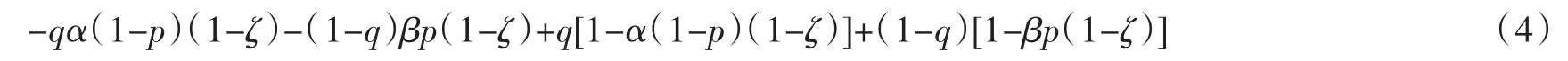
为了求得q的均衡值，我们不能将上面求得的p代入，因为这样无法求出q的均衡值，要求得这个均衡值，我们令p分别取两个特殊的边界值0和1，分别代入（4）式使其相等：

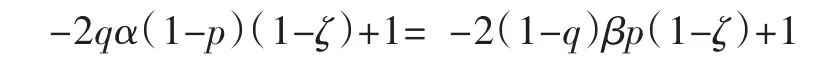
可以解得q的均衡值为：q=β/（β+α）.

自此，我们已经求出了博弈双方（守门员，射手）的混合策略（p*，q*），即：

这个混合策略纳什均衡是唯一的，也是子博弈完美纳什均衡.可以看出，由于p*/q*只与δ有关，而与μ和ζ无关，因此，这个混合策略解仅仅取决于位置变量δ，而独立于射手的技术变量μ以及守门员的技术变量ζ.

结论1：根据之前假设5当中的hα（δ）＞hβ（δ），我们也有α＞β，在这个前提下，我们将会发现，射手更偏爱于选择射远角，而守门员更偏爱于选择近角的站位.

这个结论很容易根据混合策略解得出，我们只需要对p*和q*分别关于β和α求偏导就可以了.求导之后显然有：dp*/dα＞0，dp*/dβ＜0，dq*/dα＜0，dq*/dβ＞0.因此，一方面，根据dp*/dα＞0，dp*/dβ＜0可得，如果射手往近角或者远角射门时的射门精度（α和β）越高，则门将也会更倾向于选择相应的偏向近角或者远角的站位（根据p来定义）；另一方面，根据dq*/dα＜0，dq*/dβ＞0可得，这种情况导致射手更倾向于选择相反的角度，即α或β越高，反而在混合策略中选择近角或远角的概率会越低.

结论1实际上也很符合我们平时观察到的情况，接下来，我们希望从数据统计及检验的角度来验证这个结论.

2 经验数据及检验

2.1 统计数据的来源

这种经验数据实际上就是足球比赛当中的射门得分数据，由于这种数据统计涉及到的数据量很大，要统计出一个赛季甚至几个赛季的某个联盟甚至全世界所有的足球比赛的射门数据很困难，因此，笔者在本文中将数据样本限定在2010-2011赛季英格兰超级联赛的全部进球.这样选择是因为英超是上个赛季欧洲五大联赛中进球数最多的，选择英超能够尽量增大我们的数据容量，使结果更可靠.

值得注意的是，由于我们的理论结果并不要求出现非常精细的数字结论，因此，我们只需要比较近角进球所占比例和远角进球所占比例这两个数字的相对大小就可以了.为此，我们令近角进球和远角进球的期望概率分别如下：

推论1：根据结论1，在纳什均衡时，我们应该能够观察到mβ＞mα，即远角的进球应该多于近角的进球.

在说明统计结果之前，先将进球的分类进行说明.在统计过程中，笔者将进球分为了如下几种：1）近角进球；2）远角进球；3）头球；4）任意球直接进球（包括角球）；5）乌龙；6）点球（在正中间，不存在近角远角的问题）；7）其他，例如折射等等.

之所以这样分类，是因为我们所要讨论的问题涉及到近角和远角的选择问题，并且，我们假定守门员和球员都具有一定的思考时间来进行抉择（虽然这个时间非常短）.在这种前提下，我们需要人为地排除掉一些与此不相符合的情况，例如，折射进球的角度并非射门球员原本的设想；点球是在正中间位置踢，不存在近角和远角问题；门前抢点时，守门员和射门球员都没有足够的时间去考虑站位和角度的问题等等.

根据以上分类原则，通过一些视频资料来对数据进行统计，最后得到的结果大致为：2010-2011赛季英超一共打进1063球，其中，近角进球共有117个，远角进球共有242个，另外，还有372个定位球，81个点球，36个乌龙以及其他进球.

详细的近角进球数和远角进球数统计结果如表2所示.

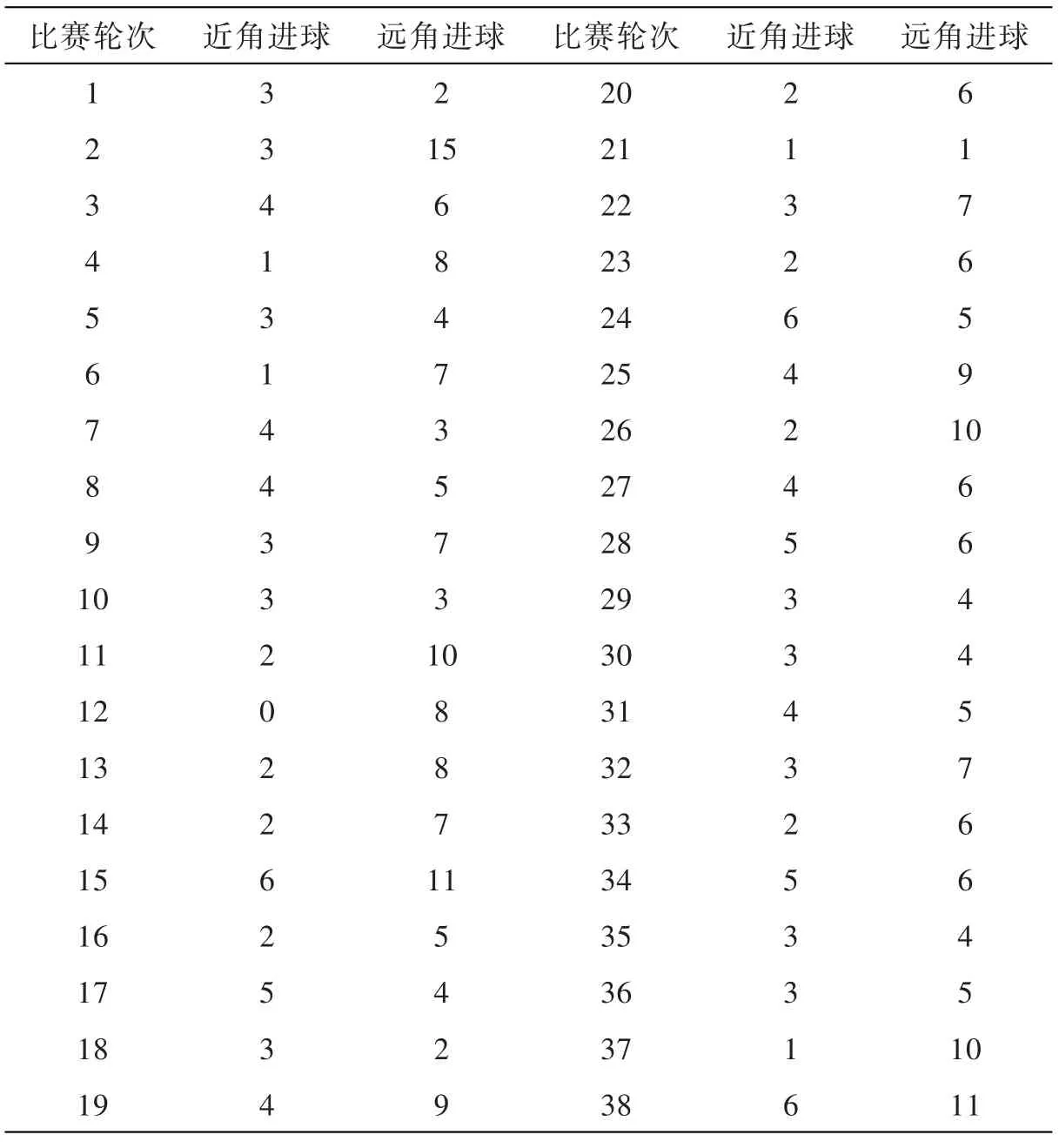
表2 2010-2011赛季英超进球类型分布

2.2 统计检验

从统计数据可以看出，远角进球的数量大约为近角进球数量的两倍，这首先为我们的结论1提供了一种直观的证据支持.

为了从统计检验的角度来考察，我们需要设定一个统计变量.为此，我们令随机变量xα代表近角进球的数量，xβ代表远角进球的数量，令近角进球的概率为ρ，则随机变量xα在α次试验中应该服从二项分布.又因为我们的总进球数为359，是一个比较大的量，所以我们可以用正态分布来近似地表达这个二项分布.我们对ρ作如下假设：

这是一个典型的单尾检验形式的假设，并且，我们需要计算如下的Z值：

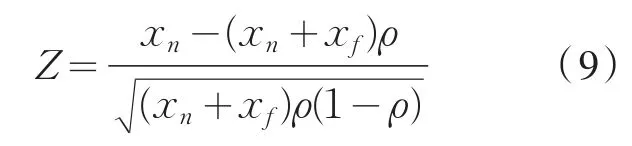
将数据 xα=117，xβ=242，ρ=1/2代入上式可得 Z=6.597.查表可得，相应的 P值约等于 3.38×10-11，这也就意味着H0很容易就能被拒绝，同时，这也意味着近角进球数所占比例显著地小于1/2.这个统计检验结果在一定程度上证明了近角进球数和远角进球数是服从我们所得到的纳什均衡模型的.

当然，以上的检验是对整体进行考察的，我们还可以更进一步地来验证每一轮比赛的进球数量分布是否也服从我们的模型.为此，我们令η=117/359，并且令yαi以及yβi分别代表每一轮比赛中近角进球数和远角进球数，其中i=1，2，3，……，38，则以下这个变量D将服从一个卡方分布：

从表2中的数据可以算出D=32.67992.同时，利用统计软件，我们可以得到相应的P值约为0.67177，这也就意味着，“每轮比赛的近角进球和远角进球分布情况都服从同一个纳什均衡解”这个结论将会很难被拒绝，或者我们可以认为，每轮比赛的近角进球和远角进球的分布情况都是服从同一个纳什均衡解的.因此，不仅在整体上我们验证了统计数据是服从纳什均衡解的，并且在局部，我们也验证了同样的结论.

3 结 论

在本文中，我们用数学模型模拟了足球比赛中球员在射门时和门将之间的博弈关系.模型的纳什均衡解显示出射手更偏爱于选择远角，而守门员更偏爱于选择近角的站位；与此同时，远角进球数会显著地多于近角进球数.之后，通过统计检验，这个理论模型的结论得到了很好的验证.

值得注意的是，本文尚存在一些问题，例如，数学建模本身存在着大量的抽象和假设，现实并没有模型所表示的这么简单；统计数据和统计检验并不是完善的；另外，最重要的是，球员毕竟是人，他们都具有自身习惯以及其他统计数据无法表现出的特征.因此，在考虑更多因素的情况下，可以对本文的模型进行更加深入和广泛的拓展.

[1]Walker M，Wooders J.Minimax play at Wimbledon[J].American Economic Review，2001，91（5）：1521-1538.

[2]Palacios Huerta I.Professionals play minimax[J].Review of Economic Studies，2003，70（2）：395-415.