乐清湾水污染物总量控制分配方法

陈慧敏,仵彦卿

(上海交通大学环境科学与工程学院,上海 200240)

乐清湾水污染物总量控制分配方法

陈慧敏,仵彦卿

(上海交通大学环境科学与工程学院,上海 200240)

从环境、自然资源、经济和社会的整体效益出发,以乐清湾COD总量控制为例建立了一种基于层次分析法的水污染物总量群决策分配方法。AHP准则层中评价指标的权重分别以专家评分法和相互重要性比较判断矩阵法来确定,子准则层中评价指标的权重分别以专家评分法、标准偏差法、熵法和理想权重优化模型来确定,从而构成各乡镇允许排污量相对于汇水区允许排污总量目标层的分配权重准则策略集。最后采用群决策博弈模型,将允许排污总量在乡镇之间进行分配。结果表明:该分配方法不仅克服了单一分配权重准则的不公平性,而且将政府决策和公众参与相结合,保证了分配依据的合理性和分配过程的公平性。

总量控制;群决策博弈;水污染物;AHP

水污染物总量控制是改善水环境质量,实现经济、社会与环境可持续发展的重要途径,亦是我国水环境管理的重要措施[1-2]。水污染物总量分配是总量控制的核心,直接影响到排污许可证的发放工作。充分考虑经济、社会、资源与环境等因素,建立公平合理的分配方法是水污染物总量控制工作得以顺利进行的关键。然而公平合理是极难衡量的概念,导致了公平准则的多元化,排污地区之间利益的冲突性,故允许排污总量分配工作一直存在较大争议。国内外学者对此也展开了广泛研究,如等比例法、建立公理体系分配法、层次分析法、基尼系数法、多目标规划法等[3-7]。

乐清湾位于浙江省沿海南部,温州湾北部,瓯江口北侧的半封闭式海湾。它包括了自乐清市岐头山咀(27°59′09″N,120°57′55″E)起,经洞头县北小门岛、大乌星 ,至玉环县大岩头灯标(28°02′16″N,121°09′09″E)连线以北的全部海域。乐清湾属亚热带季风气候区,四季分明,热量丰富,雨水充沛,地方小气候条件优越。但受季风气候不稳定影响,常有台风等灾害性天气出现。其流域总面积为1470km2,多年平均径流总量10.3亿m3。沿岸入海水系发育,注入湾内的河溪约30条,主要有大荆溪、白溪、清江、坞根溪、横山溪、江厦河、芳清河、楚门河等,大多为流程短、河床坡降大的山溪性河流。乐清湾水域的潮汐属于正规半日,潮水交换周期长导致其自净能力较差,生态环境脆弱。

根据2005年对乐清湾展开污染源普查的结果,综合考虑乐清湾自然地理、水文气象、地表水和地下水环境状况等因素,地方政府在科学确定环境容量的基础上对该海湾各汇水区“十一五“期间的允许排污量做了规定,但是将汇水区允许排污总量分配到所属乡镇的方法还存在公平性难以定量化的问题。

传统的AHP法一般采用专家评分法或者相互重要性判断矩阵法确定准则层和子准则层中评价指标的权重。由于专家评分法是一种定性的权重确定方法,相互重要性判断矩阵法是一种半定性半定量的权重确定方法,两种方法都会受到主观因素很大的影响,因此这两种方法最终确定的水污染物总量分配权重会有较大的差异。如果仅采用单一的权重确定方法,就会使参与分配的乡镇难以信服接受。此外,即使是采用定量化的权重确定方法,也会因为其方法的多样性导致最终分配方案的多样性。尽管可以设计多种分配方案的筛选方法,但是由于分配方案的筛选方法具有多样性,同样会导致最优方案的不确定性,进而影响分配方案的实施。针对以上问题,笔者采用多种方法(包括定性和定量方法)确定AHP体系中准则层和子准则层中的评价指标权重,从而构成各乡镇允许排污量相对于目标层的分配权重准则策略集,最后用群决策博弈模型对允许排污总量在乡镇之间进行分配。这种基于AHP法的水污染总量群决策分配方法相当于政府提供多种科学的分配权重方案供参与允许排污量分配的乡镇选择,而乡镇之间通过公平的博弈过程,获得确定的允许排污量,从而既解决了单一权重准则确定分配方案的不公平性,又避免了筛选方案的设计。

1 总量控制分配方法

1.1 AHP结构体系建立

将汇水区允许排污总量作为AHP的目标层A,将环境状况、自然资源、经济因素和社会因素评价指标作为准则层B,将工业排污量、农业排污量、生活排污量等实现总目标的15个具体评价指标作为子准则层C,将汇水区各乡镇作为决策层D,从而建立AHP结构体系,如图1所示。

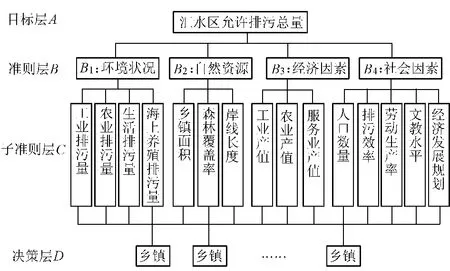
图1 AHP结构体系

1.2 评价指标权重的确定方法

AHP结构体系建立后,就确定了上下层指标之间的从属关系。首先分别用专家评分法和相互重要性判断矩阵法确定准则层B的评价指标B1,B2,B3,B4对目标层A的权重bm(m=1,2,3,4)。然后用专家评分法,标准偏差法、熵法和理想权重优化模型确定子准则层C中各评价指标(依次分别以C1,C2,C3,…,C15表示)相对于准则层B中对应评价指标的权重cj(j=1,2,…,15)。再计算子准则层C中各评价指标相对于目标层A的权重wj,其中wj=bmcj,以及n个乡镇对子准则层C中各评价指标的贡献率 ¯pij(i=1,2,… ,n),其中为乡镇对应子准则层各评价指标的数值。最后计算决策层D中各乡镇污染物分配权重Wi,其中因为准则层B中评价指标的权重有2种确定方法,子准则层C中评价指标的权重有4种确定方法,所以可得到8种权重分配准则。于是汇水区允许排污总量按照Wi在乡镇之间分配。

1.2.1 专家评分法

选择20个专家进行评分,函发咨询表20份,得到准则层B和子准则层C中关于乡镇COD分配的评价指标权重b和c分别为:

1.2.2 相互重要性判断矩阵法

采用5级标度法确定评价指标之间两两比较的相对重要性,构成的A-B判断矩阵如下:

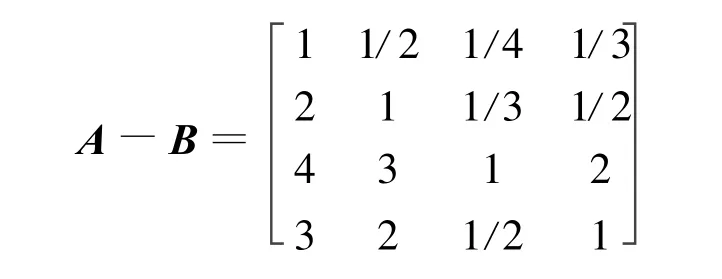
用Matlab可解出其特征向量为[0.1661,0.2787,0.8135,0.4826],最大特征值 λmax=4.0310,归一化后可得到准则层B各评价指标权重分别为0.0954,0.1601,0.4673,0.2772,一致性比率

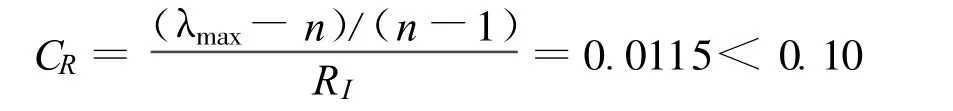
式中:n为判断矩阵阶数,这里取4;RI为平均一致性指标,查表[8]取0.9。

1.2.3 标准偏差法[9]

先将子准则层评价指标分为效益和成本型两类,再将乡镇对应子准则层C的评价指标下的数值归一化。效益和成本指标归一化方法,分别如式(1)和式(2)所示。

效益指标归一化:

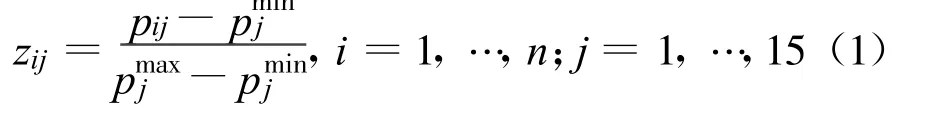
成本指标归一化:

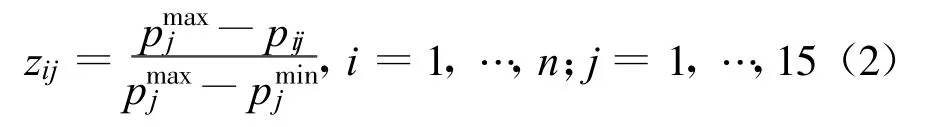
式中:pij为各乡镇对应于子准则层C中评价指标的数值;pjmin为各乡镇对应于子准则层C中评价指标的数值中的最小值;pjmax为各乡镇对应于子准则层C中评价指标的数值中的最大值;zij为pij归一化后的数值;n为乡镇总数;i为乡镇序数;j为子准则层中评价指标序数。

最后用标准偏差法确定子准则层C中评价指标相对于准则层B中对应评价指标的权重cj,如式(3)和式(4)所示。

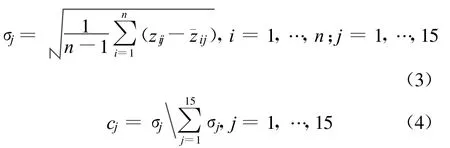
1.2.4 熵法[10]

先将子准则层C中评价指标分为效益和成本型两类,再将乡镇对应子准则层C中评价指标的数值归一化。效益和成本指标归一化方法,分别如式(5)和式(6)所示。最后计算子准则层C中评价指标的熵值Ej和其相对于准则层B中对应评价指标的权重cj,如式(7)和(8)所示。式(5)～(8)中的pij,zij,n,i,j等物理含义与式(1),(2)相同。

效益指标归一化:

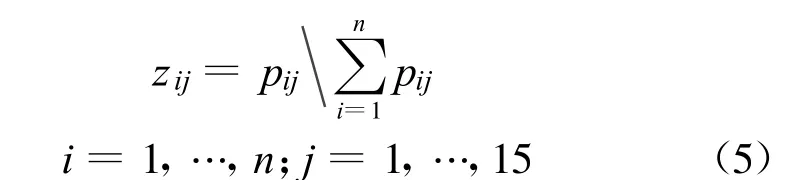
成本指标归一化:

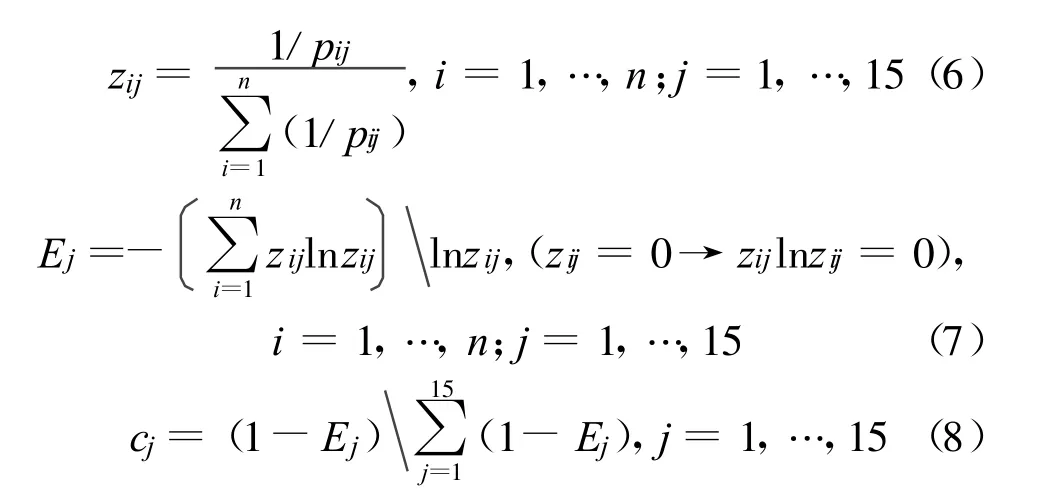
1.2.5 理想权重优化模型[11]

先将子准则层C中评价指标分为效益和成本型两类,再将乡镇对应子准则层评价指标下的数值归一化。效益和成本指标归一化方法如前面的式(1)和式(2)所示。最后用理想权重优化模型计算子准则层C中评价指标相对于准则层B中对应评价指标的权重cj的最优解,如式(9)所示。

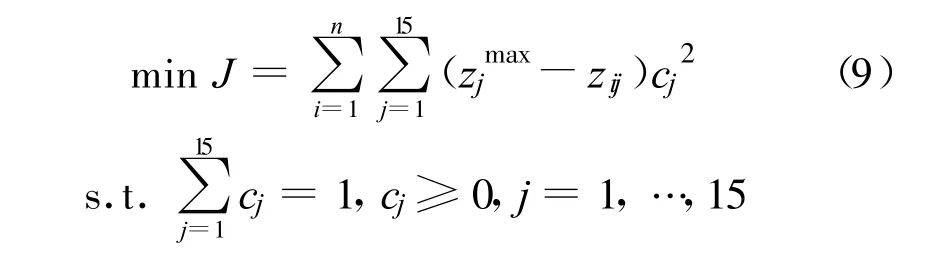
式中:J表示以cj平方和线性方程数值最小化为目标;zjmax为乡镇对应子准则层C中评价指标的数值归一化后得到zij的最大值。

由式(9)可计算出模型的最优解c*j,如式(10)所示。

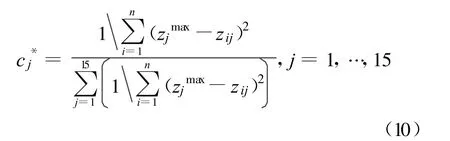
1.3 群决策博弈模型

由1.2节可确定AHP结构体系中各乡镇污染物分配权重Wi,并且由乡镇8种分配准则构成策略集。对乡镇k进行排序,假设排列为(k1,k2,…kn)。排污乡镇按顺序依次自由选择权重准则,并获得相应的允许排污量。乡镇所有选择顺序共有n!种,在整个博弈过程中乡镇选择分配准则的各种顺序都出现过,决策机会是平等的。乡镇最终污染物分配量为各种排序下博弈结果的平均值。乡镇根据个体利益最大化原则按顺序选择权重准则的博弈过程如下[12]:

a.排污乡镇k1首先决策,选择对其最有利的权重准则以获得最大允许排污量。然后乡镇k1退出该次分配,供其余乡镇分配的排污量则相应减小;

b.排污乡镇k2决策,也选择对其最有利的权重准则并获得相应允许排污量,然后退出该次分配;

c.依此类推,每个排污乡镇均选择对其最有利的准则,然后退出本次分配。在汇水区允许排污总量的约束条件下,最后1个排污单位kn获得剩余的允许排污量,不存在准则选择问题。在以上的博弈过程中,排污乡镇的次序越前,决策越主动,分配结果对其越有利。

群决策博弈模型流程如图2所示。

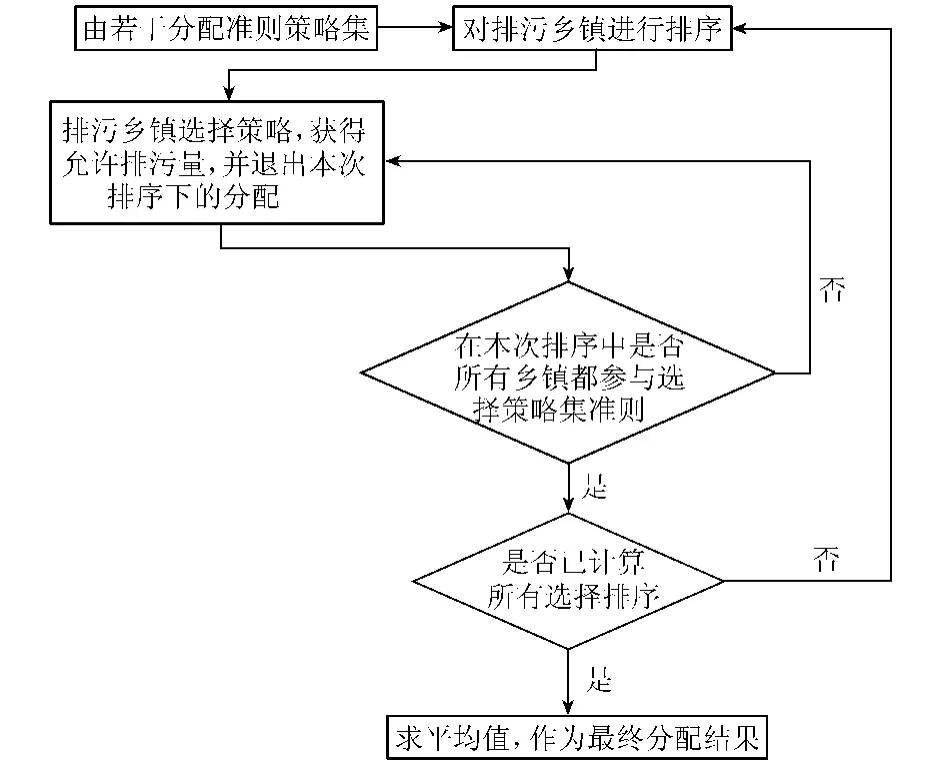
图2 群决策博弈模型流程

2 总量分配模型应用

2.1 基本资料

乐清湾和其所划分的汇水区地理位置,如图3所示。

虹桥水系汇水区是乐清湾10个汇水区之一,其包括淡水镇、虹桥镇、石帆镇、蒲岐镇、四都乡和天成乡等6个乡镇。2010年虹桥水系COD允许排放总量为5086.71t,2005年各评价指标信息如表1所示。

2.2 COD总量控制分配

根据前述的总量分配方法,可以计算出虹桥水系COD的乡镇8种分配权重,如表2所示。用Matlab编程计算出的群决策博弈模型最终分配结果如表3所示。从表3可知,2010年6个乡镇COD的允许排放量分配权重分别为0.1526,0.398 7,0.125 3,0.1539,0.0827,0.086 7,因此虹桥镇允许排污量最大,天成乡最小。

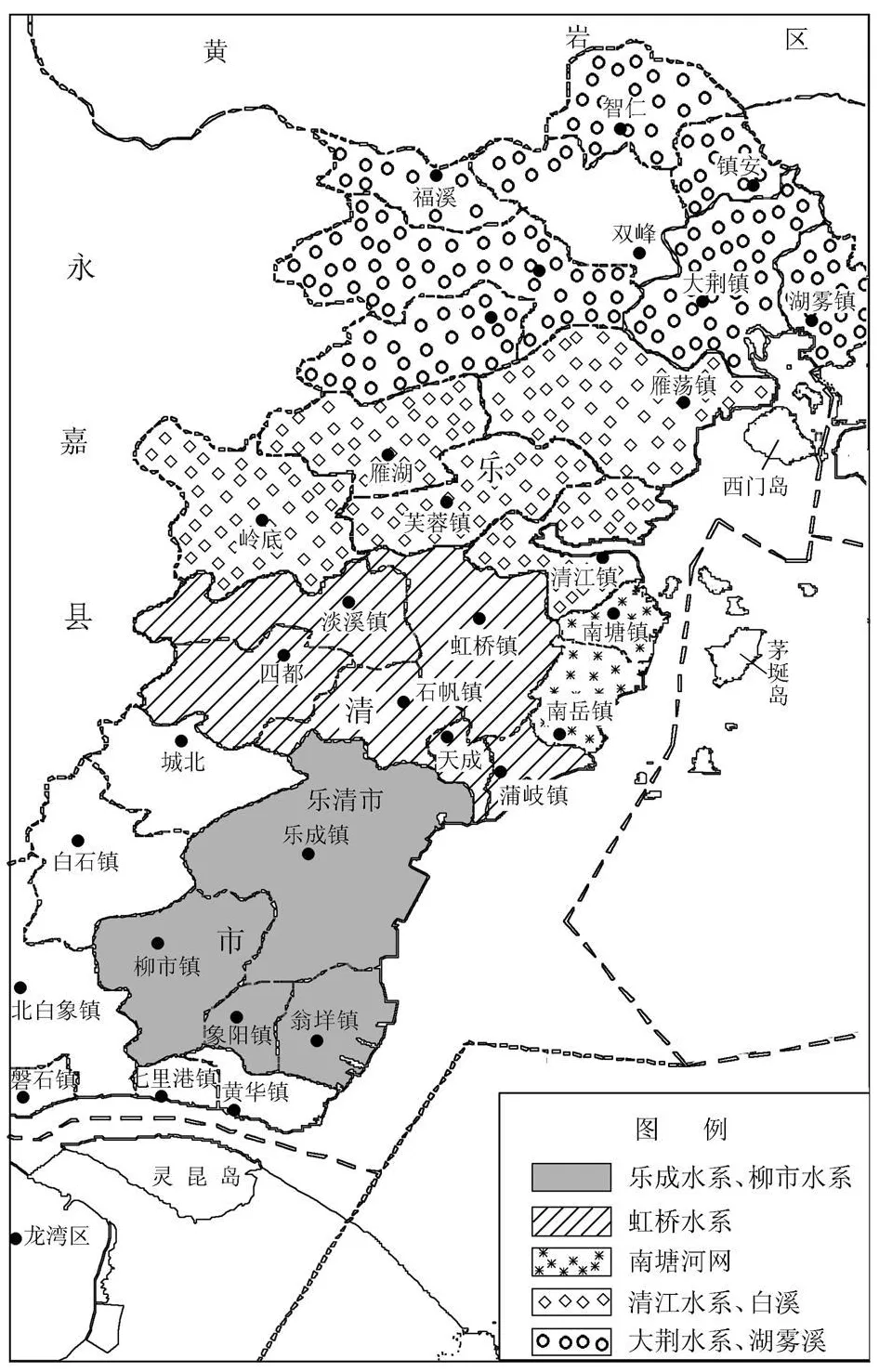
图3 乐清湾及其汇水区地理位置示意图

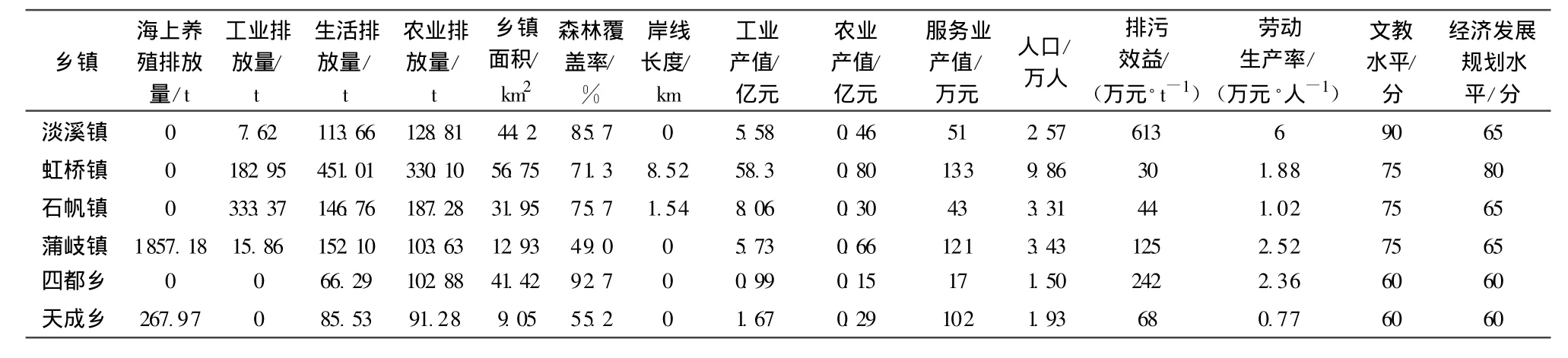
表1 虹桥水系乡镇污染物分配基本数据

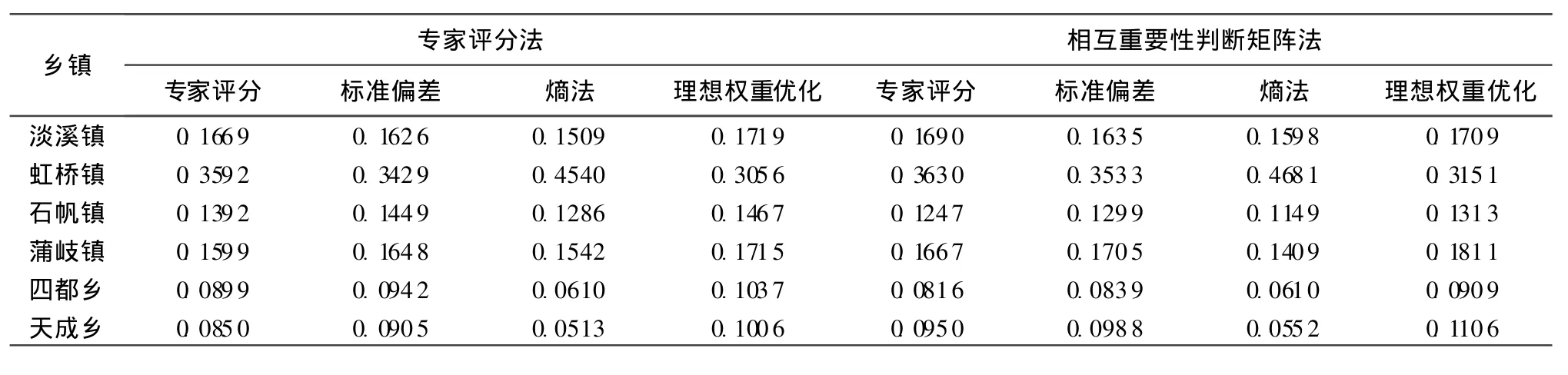
表2 用不同方法确定的乡镇COD分配权重

表3 群决策博弈模型分配结果

3 结 论

a.根据获得数据,设计了基于环境、自然资源、经济和社会因素的AHP法进行污染物总量群决策分配,同时采用不同方法确定准则层和子准则层中评价指标权重,形成分配权重准则策略集,避免了单一权重确定方法引起的不公平性。通过乐清湾虹桥水系乡镇COD总量分配实例应用,证实了该分配方法的可行性。

b.采用群决策博弈模型,无须在分配权重准则策略集中筛选出最优权重准则,提高了污染物总量控制工作的效率,避免了筛选方案设计多样性而导致的最优方案的不确定性。同时群决策博弈过程将政府决策和公众参与相结合,通过群体决策得到最终结果,因此既保证了分配准则的合理性,又保证了分配过程的公平性。

c.由于乐清湾调查资料不完善,因此对于评价指标的选择有限,指标体系有待丰富和完善,使其更具有代表性。此外,评价指标权重的确定方法有待进一步补充,从而使分配准则策略集更加丰富。

[1]李如忠,钱家忠,汪家权.水污染物允许排放总量分配方法[J].水利学报,2003(5):112-115.

[2]范平,吴纯德,张帆,等.南方某城市水污染物总量控制分配研究[J].水资源保护,2009,25(4):20-23.

[3]汪俊启,张颖.总量控制中水污染物允许排放量公平分配研究[J].安庆师范学院学报,2000,6(3):37-38.

[4]林巍,傅国伟,刘春华.基于公理体系的排污总量公平分配模型[J].环境科学,1996,17(3):35-38.

[5]范英宏,杨志峰,杨晓华,等.基于层次分析的方差赋权法的理论及其应用[J].环境科学与技术,2008,31(6):135-137.

[6]王丽琼.基于公平性的水污染总量分配基尼系数分析[J].生态环境,2008,17(5):1796-1801.

[7]崔正国.环渤海13城市主要化学污染物排海总量控制方案研究[D].青岛:中国海洋大学,2008:77-89.

[8]胡明甫.AHP层次分析法及MATLAB的应用研究[J].钢铁技术,2004(2):43-46.

[9]XU X.A note on the subjective and objective integrated approach to determine attribute weights[J].European Journal of Operational Research,2004,156:530-532.

[10]WANG Ying-ming,LUO Ying.Integration of correlations with standard deviations fordetermining attributeweightsin multiple attribute decision making[J].Mathematical and Computer Modelling,2010,51:8.

[11]WU Z,CHEN Y.The maximizing deviation method for group multiple attribute decision making under linguistic environment[J].Fuzzy Sets and Systems,2007,158(14):1608-1617.

[12]林高松,李适宇,李娟,基于群决策的河流允许排污公平分配博弈模型[J].环境科学学报,2009,29(9):2011-2016.

Allocation approach for the total amount control of water pollutants in Leqing Bay

CHEN Hui-min,WU Yan-qing
(College of Environmental Science and Engineering,Shanghai Jiaotong University,Shanghai 200240,China)

For the overall benefitsof environment,natural resources,economy and society,the group decision allocation approach for the total amount control of water pollutants based on an analytic hierarchy structure process(AHP)was established using COD total amount control in Leqing Bay as an example.The weight of indexes in the criteria level of AHP was determined by expert rating method and method of comparative judgment matrix of mutual importance respectively,while the weight of indexes in the sub-criteria level was determined by expert rating method,standard deviation(SD)method,entropy method and ideal weight optimization model,respectively.The set of target level allocationweight rules of allowable waste load of each township relative to total allowable waste load in catchment area was constructed.The permitted amount of pollutants was allocated among townships through the group decision game model.The results showed that the approach not only overcomes the unjustness due to using the single weight distribution method,but also the reasonablenessof allocation rules and justice of allocation process were guaranteed by combination of the governmental decisionwith public participation.

total amount control;group decision game;water pollutants;AHP

X32

A

1004-6933(2011)03-0049-05

10.3969/j.issn.1004-6933.2011.03.012

国家海洋公益行业科研专项(20080506)

陈慧敏(1984—),女,福建福州人,硕士研究生,研究方向为水资源与管理。E-mail:chenhm668@sina.com

(收稿日期:2010-04-04 编辑:高渭文)