我国铁路运输与第二产业发展的动态关系研究

张凌洁，马立平

（首都经济贸易大学 统计学院，北京 100026）

目前，我国处于工业化加速发展时期，第二产业比重稳步上升并居国民经济的主体地位。作为现代经济运行重要组成部分的铁路运输，密切影响着第二产业的发展。从经济规模上，第二产业的生产规模代表区域内部的货物生产规模，而货物生产规模与货物周转量有直接关系。无论这些货物是作为居民最终消费使用，还是作为其他产业的中间产品投人使用，均会带来区域的货物运输需求。第二产业的行业集中度与货物周转量有密切的关系。目前，国内相关研究大多是定性地分析铁路运输业在国民经济中的重要地位，定量研究尤其是动态研究较少。因此，结合我国1978—2008 年铁路运输指标数据和第二产业增加值年度数据，基于 VAR 模型，运用协整理论、脉冲响应函数来研究其动态影响关系。

1 模型研究及应用

采用向量自回归模型 (Vector Auto-regression，VAR)，选用货运量和货物周转量x2作为研究铁路运输业的指标，全国第二产业增加值y作为第二产业经济发展的指标。将第二产业增加值、货运量、货物周转量这3个变量通过 VAR 模型的脉冲响应函数和方差分解技术，研究第二产业与铁路运输的相互响应关系及程度。为保证数据的可比性，以 1978 年为基期，计算得到各年实际增加值，再进行对数变换，然后分别把lny、lnx1和 lnx2的一阶差分记为Δlny、Δlnx1和Δlnx2。

1.1 时间序列平稳性及其检验

时间序列的平稳性是指时间序列的统计特性不随时间推移而发生变化的特性。采用增广迪基-福勒检验 (Augmented Dickey-Fuller test，ADF检验)来判断时间序列的平稳性，ADF检验用于检验序列是否服从有单位根的自回归过程。下面分别对序列lny、lnx

1、lnx2进行检验，结果表明三者均不是平稳序列；再分别对序列Δlny、Δlnx1和Δlnx2进 行

ADF 检验，说明三者均为一阶单整序列，检验结果如表1所示。

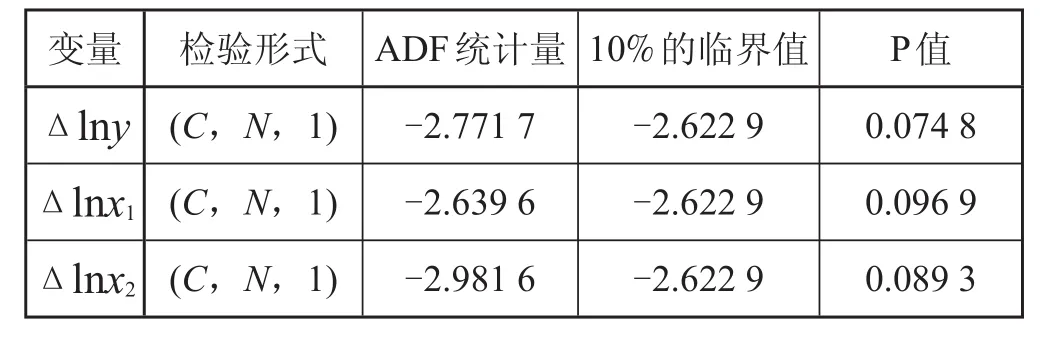
表 1 ADF 检验结果

注：检验形式 (C，N，1) 中的C、N和1分别表示单位根检验方程，包括常数项，不包括时间趋势，滞后阶数为 1。

1.2 确定向量自回归模型阶数

VAR 模型采用多方程联立的形式，在每个方程中将每个内生变量对模型的全部内生变量的滞后值进行回归，从而估计全部内生变量间的动态关系。VAR 模型除需要满足平稳性条件外，还应确定滞后期k。如果滞后期太少，误差项的自相关会很严重，并导致参数的非一致性估计。本研究对最优滞后期的选择根据赤池消息准则 (AIC) 和施瓦茨准则 (SC) 来确定，当两者达到最小时的阶数为最优阶数。通过检验可以看出，最优阶数为3。

1.3 协整检验

在模型中3个变量同阶单整，满足协整检验的前提条件，为了探索变量之间是否具有长期的稳定关系，需要进行协整检验。本研究采用基于 VAR模型的 Johansen 协整检验。协整检验模型实际上是对无约束 VAR 模型进行协整约束后得到的 VAR 模型，该模型的滞后期是无约束 VAR 模型一阶差分变量的滞后期。由于无约束 VAR 模型的最优滞后期为k，所以将协整检验的 VAR 模型滞后期确定为k-1。本研究确定模型滞后期为 2，采用无截距和趋势项的检验方式。从表2中可以看出，在 5% 的显著性水平下，迹检验和最大特征根检验都认为变量之间不存在协整关系，这说明第二产业的发展与货运量和货物周转量的发展之间不存在长期的均衡关系。

1.4 建立向量自回归模型 (VAR)

由于Δlny、Δlnx1和Δlnx

2均可看作内生变量，因此可以建立二阶的无约束 VAR 模型。经过检验，模型是显著的，说明该 VAR 模型的结构是稳定的。通过基于 VAR 模型的脉冲响应函数和方差分解，可以测算Δlny对Δlnx1和Δlnx

2冲击的响应。观察特征根的分布，模型特征根均小于 1，说明模型的结构是稳定的，可以进行脉冲响应分析与方差分解分析。

1.5 脉冲响应函数

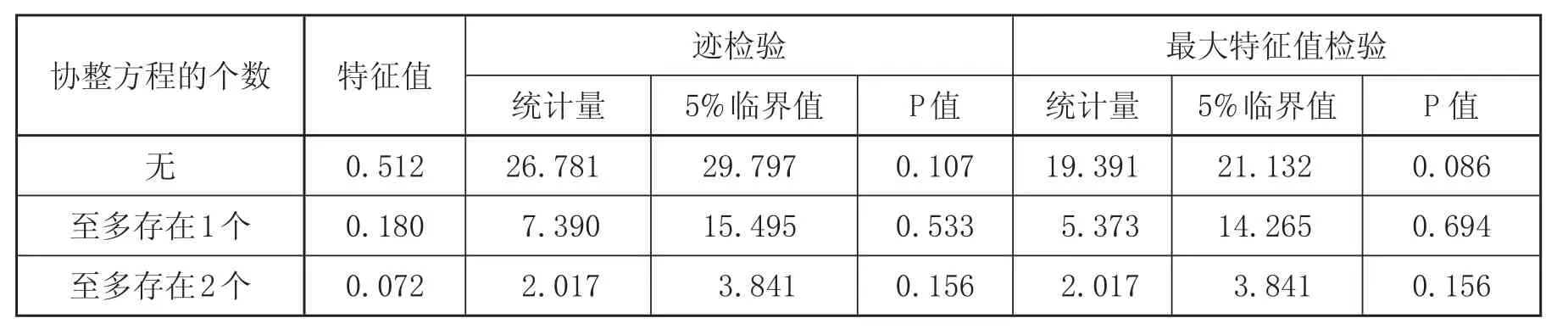
表 2 Johansen 协整检验

脉冲响应函数是用于衡量随机扰动项的一个标准差冲击对其他变量当前和未来取值的影响轨迹，能够比较直观地刻画出变量之间的动态交互作用及效应。

基于 VAR (3) 模型运用模拟冲击法，对系统施加外部冲击，计算各变量对冲击的反应，并将各变量的瞬时反应加总，考察其对外部冲击的长期总反应。图1—图5分别表示Δlny对Δlnx1、Δlnx2对一个标准差随机扰动项的累积脉冲响应，即分别显示了其对自身和其他变量的标准差冲击的长期总反应。在图 1—图5中，上下两条虚线分别代表正负 2倍标准差偏离带，中间实践代表脉冲相应函数，在模型中将响应的时间长度设定为 15 年。模型通过显著性检验且调整的可决系数均大于 0.95。

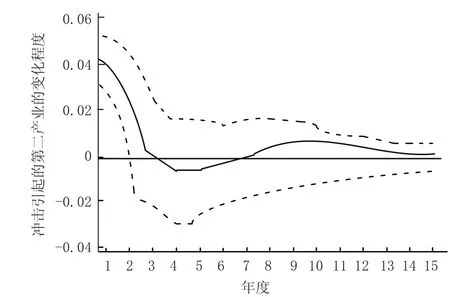
图 1 第二产业对其自身一个标准差的脉冲相应图

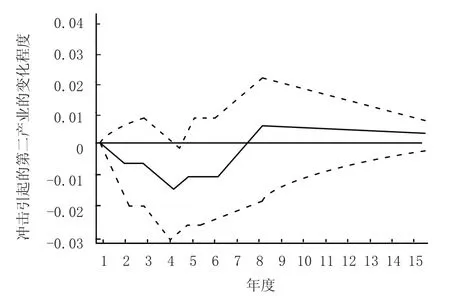
图 2 货物周转量对第二产业的脉冲相应图

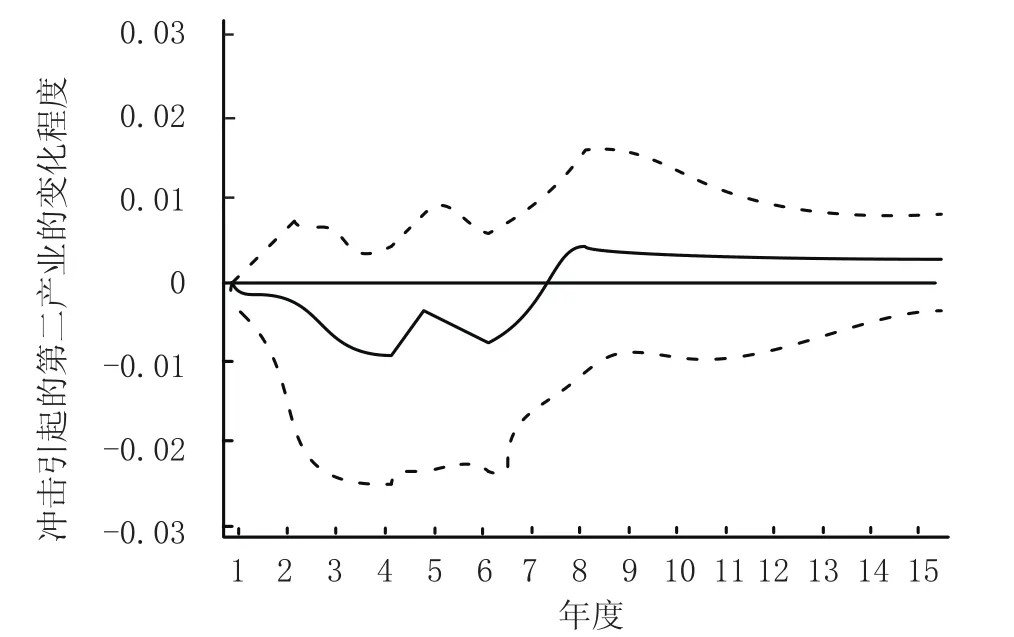
图 3 货运量对第二产业的脉冲相应图

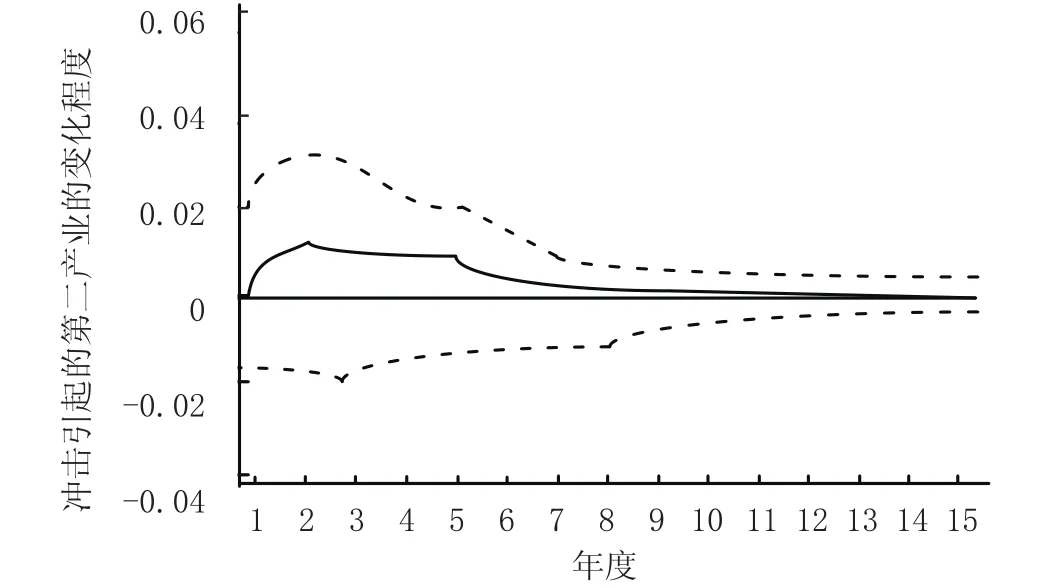
图 4 第二产业对货物周转量的脉冲相应图

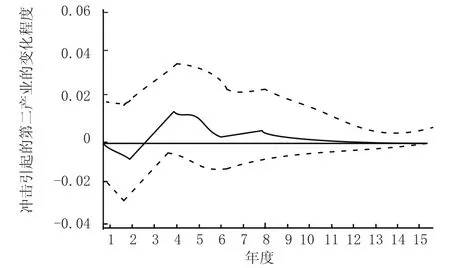
图 5 第二产业对货运量的脉冲相应图

从图1可以看出，第二产业增加值对其自身一个标准差的冲击响应开始是正的响应，到第三期由一个小小的波动变为负相应，第七期转为正向，慢慢收敛。从图2可以看出，货物周转量的冲击引起经济增长变化的脉冲响应过程是当在第一期给货物周转量一个标准差的冲击后 (即货物周转量增加)，对经济增加值是一个负响应，在第四期到达顶点后逐渐收敛并转为正向收敛。从图3可以看出， 货运量的冲击引起经济增加值的变化的脉冲响应过程是当在第一期给出一个标准差的冲击，对经济增加值是一个负响应，在第四期到达顶点后逐渐收敛，到第七期出现正响应并趋于平稳。图4、图5是第二产业增加值对货运量、货物周转量的脉冲响应图，在第一期给出经济一个标准差的冲击后，从第二期开始对货运量一直呈现正向效应，并且快速收敛，达到稳定状态；第二产业增加值对货物周转量有短期的负向效应，第三期即为正向效应并快速收敛达到稳定状态。

1.6 方差分解

方差分解表示当系统的某个变量受到一个单位的冲击以后，以变量的预测误差方差百分比的形式反映向量之间的交互作用程度，其基本思想是把系统中每个内生变量的变动按其成因分解为与各方程随机扰动项相关联的各组成部分，以了解各随机扰动项对模型内生变量的相对重要性。利用方差分解技术分析铁路运输对第二产业增加值的贡献率 (见表3)。

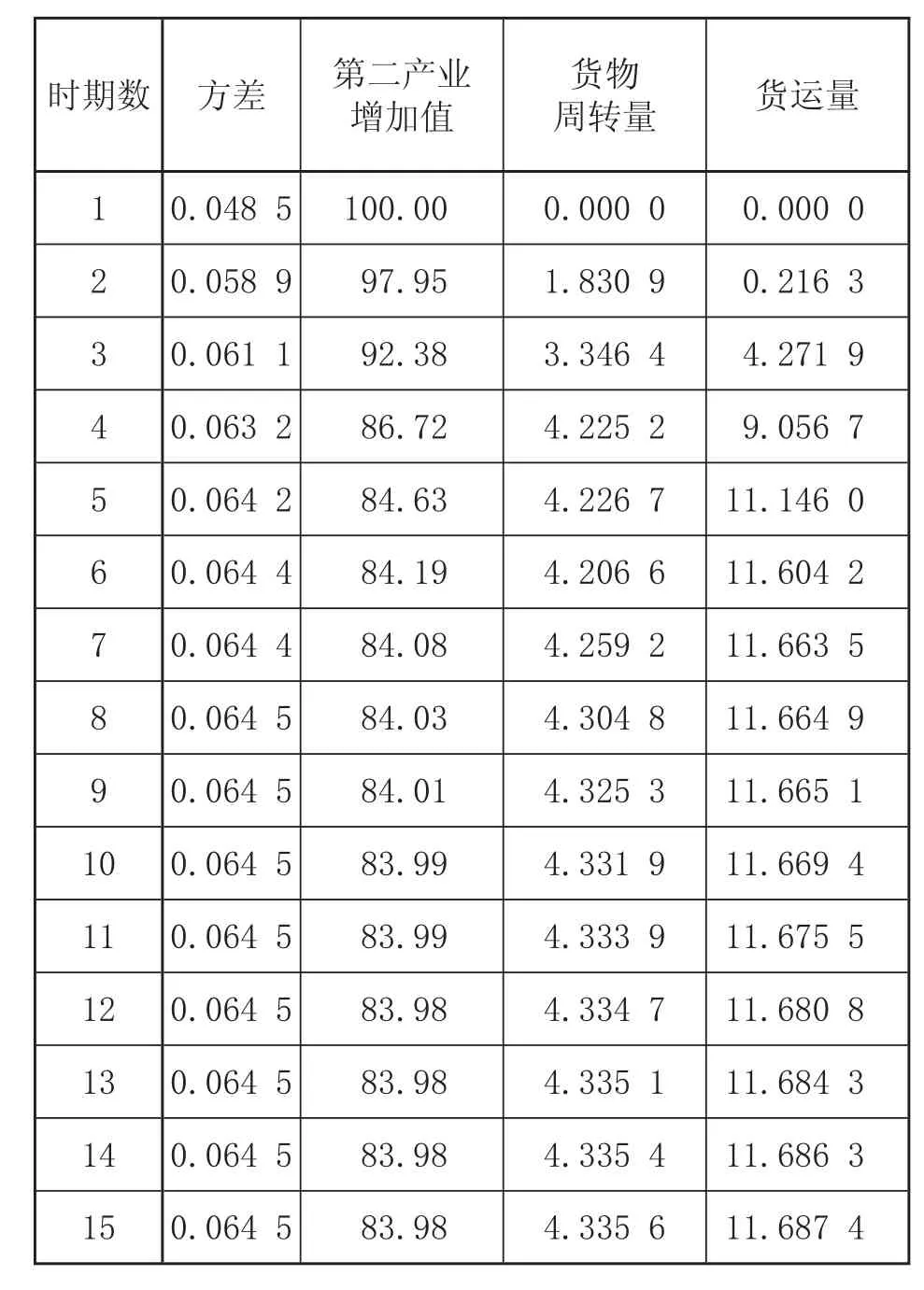
表 3 第二产业增加值的方差分解表

从表3中可以看出，第二产业增加值的波动在第一期只受自身波动冲击的影响，这是由于在建立VAR 模型时，把Δlny作为第一个因变量，从第二期开始来自第二产业增加值自身的扰动逐渐下降，在第四期受自身影响显著下降，在第十期后基本稳定在 83% 左右，但仍起主要作用，这与脉冲响应的结论相一致。货运量变化从长期来看，能够影响第二产业增加值变化的 11.69% 左右；而货物周转量对第二产业增加值变化的影响程度能力较小，仅为4.34% 左右。

2 基本结论

基于 1978—2008 年的第二产业增加值和货运量与货物周转量数据，对以上变量采用时间序列的平稳性检验、协整检验的实证分析表明，第二产业增加值和货运量与货物周转量三者之间并不存在协整关系。同时，构建了第二产业和交通运输的VAR(3) 模型，并在此基础上利用脉冲响应函数分析了3个变量之间的关系，对因变量预测误差进行分解得出以下结论。

（1）在 5% 显著水平上，第二产业增加值和货运量与货物周转量并不存在长期稳定的均衡关系；从长期来看，第二产业增加值不仅能自我促进，而且对货运量与货物周转量发展有显著正效应，这不仅说明我国的经济增长具有一定的惯性，而且反映出经济增长的预期水平对铁路运输部门经济实际运行态势具有显著影响。

（2）货运量和货物周转量对第二产业增加值的初期呈现负效应，到达第七期时才转向正向效应，但效果并不显著，说明铁路运输业对第二产业增长的促进效应仍未激活。通过对第二产业增加值的方差分解，引起其发生变化的主要原因是自身的随机扰动项冲击和货运量冲击，货物周转量的贡献率非常小。

3 结束语

通过分析，货运量和货物周转量对第二产业增加值的促进效应并不十分显著，第二产业主要是靠自身的内生增长。因此，从长期来看，铁路建设应着力外延扩张，结合区域产业结构调整，优化运输资源配置，这将促使铁路运输业与第二产业之间的关联度更加紧密，起到相互带动的长期作用。