基于卡尔曼与改进SVM移动机器人定位研究*

王春荣，蔡 勇，蒋 刚

（西南科技大学 制造科学与工程学院，四川 绵阳621010）

对于在动态环境中的移动机器人来说，定位技术是一项最基本、最重要的功能。因此,研究移动机器人的自主定位具有很重要的意义。

机器人的定位[1]技术分为两类：相对定位和绝对定位。相对定位是由编码器、里程计等传感器与机器人前一时刻的位姿来推出下一时刻的位姿。绝对定位是采用摄像头和激光超声波等传感器,然后根据已知位置的标志物进行定位,需要对环境的先验知识。由于单传感器都有局限性，因此采用多个传感器进行融合以达到较准确的定位技术。本文将讲述利用卡尔曼滤波算法将编码器测得的机器人航向角和陀螺仪测得的机器人航向角进行滤波融合[2]，修正因轮子打滑等引起的编码器测角误差，再经过LS_SVR建立回归曲线，提高定位精度。

1 系统定位模型的构建

差动驱动式移动机器人的几何模型如图1所示。

根据图1所示则有：

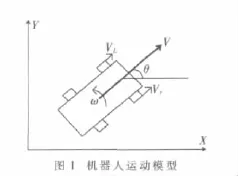
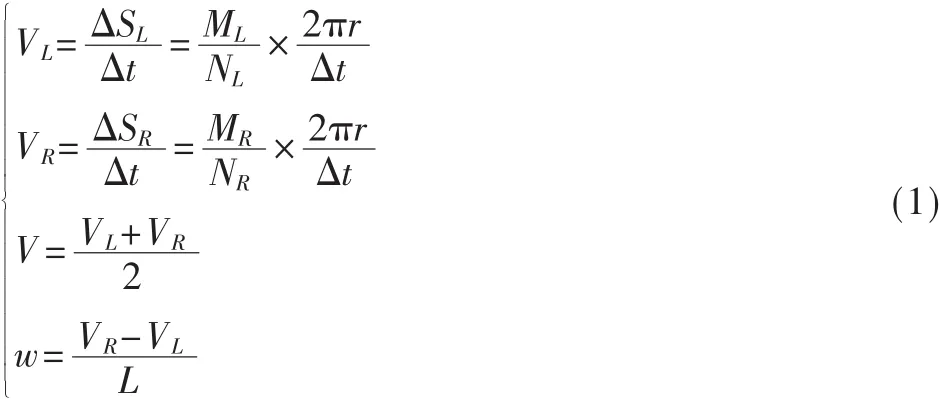
其中，NL是编码器的线数，ML和MR分别为Δt时间内左右两个编码器输出的脉冲数，L为左右两个驱动轮之间的距离，r为驱动轮的半径，VL为机器人左边两轮的线速度，VR为机器人右边两轮的线速度，w为里程计测得的机器人航向变化的角速率，θk为机器人的航向角。

一般差动机器人的位置 p=[x，y，θ]T可以从一个已知的位置开始，然后对其运动积分来估计下一时刻的位置。若采样周期为Δt的离散系统，则位置增量为：

系统的定位模型为：

2 定位算法

2.1 卡尔曼滤波器

卡尔曼滤波[3，4]是由 KALMAN R E于 1960年提出的一种有噪声线性动态系统状态预估的递归算法，它是一个不断预测与校正的过程。

用卡尔曼滤波器来融合码盘和陀螺仪数据，设状态变量为：

式中，ω为陀螺仪测得的角速度，则系统的状态方程为：

式中，ΦK+1/K为 tK时刻到tK+1时刻的状态转移矩阵，本系统中为：

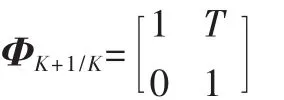
WK是协方差为Q的系统噪声矩阵；ΓK是系统噪声矩阵的驱动矩阵，本系统中为I。

系统的量测方程为：

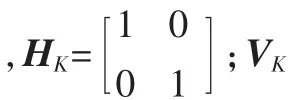
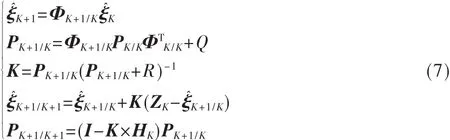
式中，P为误差协方差矩阵，K为卡尔曼增益矩阵。

通过式(7)可以计算出系统变量的估计值，将估计值代入公式（3）中，即可得到融合后的码盘推算值。

2.2 最小二乘支持向量机

最小二乘支持向量机[5,6]与标准支持向量机的最大不同之处是前者把不等式约束变成等式约束，而且把经验风险由偏差的一次方改为二次方。给定训练集：

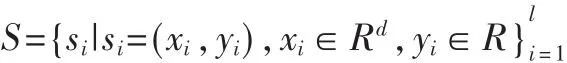
通过高维特征空间中的线性函数

来拟合样本集，因此在最小二乘支持向量机中，回归问题可表述为约束优化问题，即：

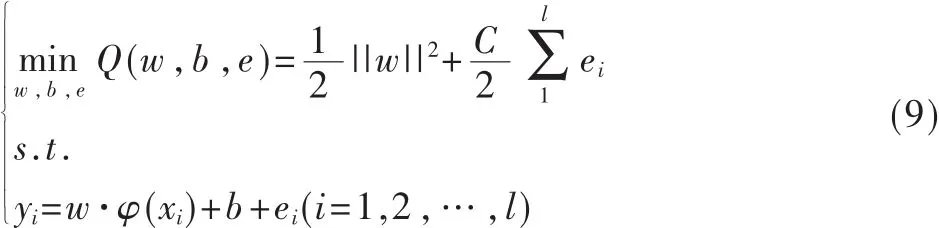
要求解式（8）的优化问题，把约束优化问题转变成无约束优化问题，从而建立Lagrange函数：

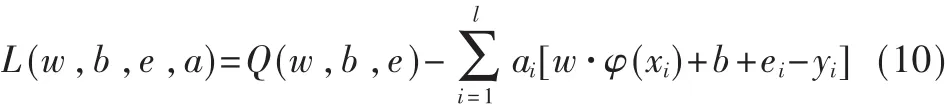
根据KKT条件有：

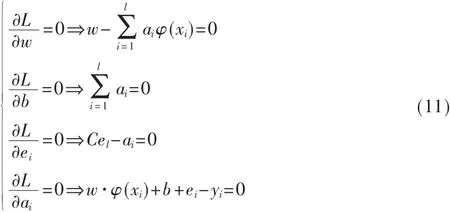
在方程（11）中消去 ei、w，即得到：

其 中 ：y=(y1，y2， … ，yl)T，∧=(1，1， … ，1)T，a=(a1，a2，…，al)T，Qij=[φ(xi)·φ(xj)]=K(xi，xj)，i，j=1，2，…，l即支持向量机的输出为：

因此，最小二乘支持向量机的训练问题不像标准支持向量机那样要求解一个二次型规划问题，而是归结为一个线性方程组的求解问题，这样就变得更为简单快速。

因此定位算法步骤如下：

(1)设置系统状态变量的初始值ξ0，及其误差协方差P0，系统噪声协方差Q0，以及观测噪声协方差 R0；

(2)Kalman滤波完成一步预测计算预估状态ξ^-以及计算先验误差协方差；

(3)Kalman滤波进行测量更新，分别计算增益K、更新后的状态估计和更新后的误差协方差；

3 实验及分析

本系统用Matlab对机器人的行走的航向角和路径进行仿真实验。首先假设系统噪声是相互独立而且是零均值的高斯白噪声，因此协方差矩阵Q为对角矩阵。状态变量初始值取所采集数据滤波前的均值，则：

估计误差初值取滤波前的均方差和4%的均方差，则：

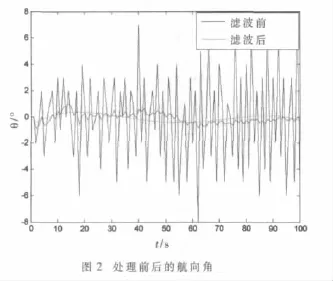
实验方法：以铺着鹅卵石的水泥地为实验平台，设定好全局坐标及将机器人的起始航向角记为0，然后通过编码器实现机器人的直线和转弯行走。图2所示为机器人直线行走时航向角的变化，可以看出经过卡尔曼滤波和最小二乘支持向量机回归之后的航向角误差在1°以内。图3所示为机器人的轨迹图，可明显看出处理完之后的轨迹很接近于理论的轨迹。

本文将卡尔曼滤波和最小二乘支持向量机相结合实现了对机器人的定位。卡尔曼滤波是一种递推估计算法，主要思想是利用前一时刻的估计值和现时刻的观测值来更新对状态变量的估计，求出现时刻的估计值,经实验证明有较好的效果。但是,在本文中所采用的定位方法只是相对定位方法,随着时间的增加就会有误差的累积，因而可将激光超声波和摄像头等传感器加入机器人定位系统,采用相对定位和绝对定位相结合,来消除经长时间运行而产生的累积误差。

[1]历茂海,洪炳熔.一种鲁棒的室内移动机器人定位方法[J].计算机工程与应用,2005，42(4)：1-4.

[2]王军,苏剑波,席裕庚.多传感器集成与融合概述[J].机器人,2001,23(2)：183－192.

[3]陈旻.基与DSP的扩展卡尔曼滤波直流无刷电机控制[J].单片机与嵌入式系统应用，2003,3(11)：1-4.

[4]段凯宇,张力军.基于到达角 Kalman滤波的 TDOA/AOA定位算法[J].电子与信息学报，2006，28(9)：1-4.

[5]辛菁,刘丁,徐庆坤.基于 LS_SVR的机器人空间4DOF无标定视觉定位[J].控制理论与应用,2010,27(1):1-9.

[6]周松斌,刘桂雄.基于LS_SVR的无线传感器网络节点定位算法[J].制造业自动化,2008,30(9):1-5.