大口径光学元件重力变形补偿的设计分析

王汝冬，王 平，田 伟，王立朋，隋永新，杨怀江

（中国科学院长春光学精密机械与物理研究所应用光学国家重点实验室，吉林长春130033）

大口径光学元件重力变形补偿的设计分析

王汝冬，王 平，田 伟，王立朋，隋永新，杨怀江

（中国科学院长春光学精密机械与物理研究所应用光学国家重点实验室，吉林长春130033）

根据弹性板壳理论，建立了大口径光学元件的几种理论模型。提出了一种补偿大口径光学元件重力变形的方法，该方法通过在透镜镜框边缘施加作用力，使透镜产生与重力变形反向的挠性变形，抵消重力变形的影响。建立了带镜框的大口径透镜的分析模型，证明了通过优化施加力的大小和支撑点位置使透镜产生挠性变形的方法能有效消除重力变形的影响。

重力变形；挠性补偿；板壳理论；有限元法

1 引 言

随着光学加工和制造技术的发展以及科学研究和装备制造的需要，光学系统的有效口径越来越大。其中一些立式使用的光学系统如光刻机曝光镜头，其透镜元件口径很大，产生的重力变形会影响系统的成像质量；而立式大口径（＞Φ250 mm）高精度干涉仪的标准具，重力变形会影响其面形精度，因此，现在大口径光学元件的设计和制造，越来越重视重力变形对光学系统性能的影响［1～5］。大口径光学元件重力变形对光学系统的影响可以通过后期调整透镜间隔进行补偿［6］；或者通过预先分析和预测透镜的重力变形，在加工阶段进行补偿，使用时透镜经重力变形后作为所需面形。本文提出了一种补偿大口径光学元件重力变形的方法。该方法通过在透镜镜框边缘施加作用力，使透镜产生与重力变形反向的挠性变形，通过调节作用力的大小和支撑点位置来补偿透镜重力引起的面形变化。

2 透镜受力小挠性变形分析

在透镜元件受力挠性变形分析中，一般把透镜元件材料（玻璃）近似为弹性材料，因此可以应用弹性力学分析中的准则对透镜进行受力分析。对于透镜元件，如果口径较大，且厚度很小（L≫10t），则可以把大口径透镜元件当成薄板分析；当透镜元件厚度相对于直径较大时（L＜10t），透镜元件横向剪切力所引起的变形和弯曲变形属于同一数量级，薄板理论已经不再适用，需要把透镜作为中厚板分析，此时应用弹性力学的三维问题来求解［7～9］，如图1所示。

图1 透镜3种板壳模型Fig.1 Three shell theory models of lens

大口径透镜受到的重力变形相对于其厚度是极小量，属于小挠度变形范围，如果透镜的中性面曲率半径很大，且厚度较薄，透镜中性面接近于平面，如图1（a）所示，应用基于Kirchhoff-Love假设的经典弹性薄板理论，可以得出透镜元件（重力方向）的挠性变形，用极坐标表示为：

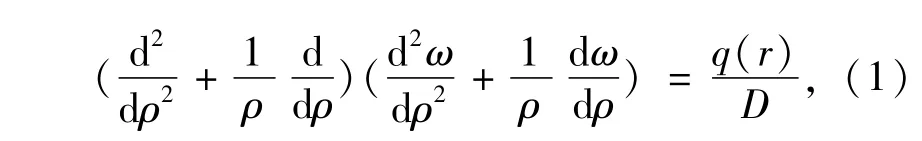
当透镜较厚，且中性面曲率半径很大，接近于平面时，如图1（b）所示，应用由Reissner模型建立的极坐标中厚板弯曲的基本微分方程，在轴对称情况下可表示为：

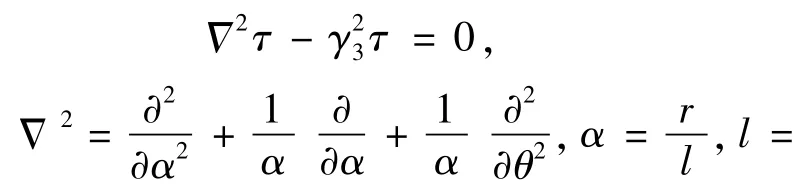
中厚板的Reissner模型公式（2）和扁壳方程（3）都是非线性问题，不能像公式（1）那样得到有效解析解，需要通过给定的边界条件，应用数值分析计算求解，一般有Fourier-Bessel级数法和摄动法等［10～12］。

3 大口径光学元件重力变形的挠性补偿仿真分析

大口径透镜通过胶粘结或者机械装夹等方法和镜框固连到一起，支撑点在金属镜框上，在镜框外边缘施加作用力，通过产生的弯矩使透镜产生与重力方向相反的小挠度变形，补偿重力变形，如图2所示。如果透镜较简单（平镜或近似平镜），可以通过公式估算出补偿重力变形所需施加力的大小；如果透镜形状较复杂可以通过数值算法或者仿真分析的方法推算出施加力的大小。

某平凸透镜，口径为Φ300 mm，凸面曲率半径约为531 mm，透镜中心厚度为35 mm，材料为熔凝石英，镜框材料为铟钢，外径为Φ480 mm，材料参数见表1。

图2 透镜镜框边缘施力示意图Fig.2 Force applied at edge of lens frame

表1 透镜、镜框材料参数表Tab.1 Martial parameters of lens and frame

图3 透镜变形分析Fig.3 Results of lens deformation

分别分析透镜凸面重力变形、镜框边缘施加约108 N力后透镜的变形，结果如图3所示。

对透镜凸面重力变形后面形和力补偿后的面形进行分析计算，移除刚体位移，得出结果如表2所示。

表2 透镜凸面面形Tab.2 PV and RMS of lens convex surface

通过表2可以看出，通过施加力使透镜产生小挠度的弯曲变形能够部分抵消重力变形，使透镜的面型质量大有改善；通过优化支撑点的位置和施加力的大小，可以得到更好的重力变形补偿结果。施加力之后透镜的最大应力约为35.7 KPa，远小于熔石英的破坏应力52.4 MPa，但是对应力双折射要求严格的某些光学系统（干涉仪、光刻镜头等），需要计算施加力后应力双折射等对光程的影响［14～16］。

4 结 论

本文提出了一种补偿大口径光学元件重力变形的方法，仿真分析证明，通过对透镜施加某一弯矩使透镜产生小挠度变形，可以部分抵消重力变形对面形的影响。两部分理论分析显示，相同挠性变形，透镜抗弯刚度越小，需要施加的力矩越小，透镜应力双折射引起的光程差就越小。不同的光学元件因外形尺寸不同，材料不同，要求不同，需要建立合理的模型进行分析来优化支撑点位置和力的大小，以达到最优的结果。

［1］武旭华，陈磊，王磊.Φ300 mm干涉仪参考镜的设计及测试［J］.光学 精密工程，2007，15（8）：1235-1240.WU X H，CHEN L，WANG L.Design and test of reference mirror in Φ300 mm interferometer［J］.Opt.Precision Eng.，2007，15（8）：1235-1240.（in Chinese）

［2］张德江，刘立人，徐荣伟，等.透镜自重变形引起波像差的有限元分析［J］.光学学报，2005，25（4）：538-541.ZHANG D J，LIU L R，XU R W，et al..Finite element analysis for wavefront error of lenses induced by gravity［J］.Acta Opt.Sinca，2005，25（4）：538-541.（in Chinese）

［3］谭凡教，乔彦峰，李耀斌，等.光电经纬仪主镜系统自重变形的有限元分析［J］.光学仪器，2007，29（6）：65-68.TAN F J，QIAO Y F，LI Y B，et al..FEM mechanical analysis for primary mirror self-weight deformation of photo-electronic theodolite［J］.Opt.Instruments，2007，29（6）：65-68.（in Chinese）

［4］雷江，蒋世磊，程刚.高精度光刻物镜的变形研究［J］.光电工程，2005，32（2）：12-14.LEI J，JIANG SH L，CHENG G.Deformation of high-accuracy photolithographic objective lens［J］.Opto-Electronic Eng.，2005，32（2）：12-14.（in Chinese）

［5］李福，阮萍，赵葆常.重力作用下平面反射镜变形研究［J］.光子学报，2005，34（2）：272-275.LI F，RUAN P，ZHAO B CH.Study on the surface deformation of flat reflector under gravity load［J］.Acta Photonica Sinica，2005，34（2）：272-275.（in Chinese）

［6］IRIE S，WATANABE T，KINOSHITA H，et al..Development for the alignment procedure of three-aspherical-mirror optics［J］.SPIE，2000，3997：807-813.

［7］江五贵，扶名福.中厚板壳非线性理论的研究进展［J］.南昌大学学报（工科版），2000，22（1）：10-16.JIANG W G，FU M F.Advances in the research of nonlinear theory of moderately thick shells［J］.J.Nanchang University（Engineering＆amp；Technology），2000，22（1）：10-16.（in Chinese）

［8］孙天祥，杨力，吴永前，等.基于弹性力学的应力加工方法有限元分析［J］.强激光与粒子束，2010，22（2）：361-364.SUN T X，YANG L，WU Y Q，et al..Finite element analysis of stressed mirror polishing based on elasticity mechanics［J］.High Power Laser and Particle Beams，2010，22（2）：361-364.（in Chinese）

［9］李婧.变厚度圆板轴对称非线性分析［D］.天津：天津大学，2004.LI J.Nonlinear analysis of spherical shells with arbitrarily variable thickness［D］.Tianjin：Tianjin University，2004.（in Chinese）

［10］周慎杰，王旭东.中厚扁球壳弯曲问题的一般解［J］.福州大学学报（自然科学版），1994，22（4）：30-35.ZHOU SH J，WANG X D.The regular solution to the bending problem of moderate thick shallow spherical shells［J］.J.Fuzhou University（Natural Science），1994，22（4）：30-35.（in Chinese）

［11］蔡长安.周边固支厚圆板受中心集中力弯曲的BESSEL级数解法［J］.贵州工业大学学报（自然科学版），2000，29（3）：5-9.CHAI CH A.Bessel series method for bending problem of a thick circular plate with fixed edges loaded by a centric concentrated force［J］.J.Guizhou University Technol.（Natural Science Edition），2000，29（3）：5-9.（in Chinese）

［12］包世华，张铜生.扁球壳在集中荷载作用下位移和内力的计算公式和数值表［J］.工程力学，1994，11（2）：51-58.BAO SH H，ZHANG T SH.Calculating formulas and numerical tables for deflection and stress resultants of shallow spherical shell under concentrated loads［J］.Eng.Mechanics，1994，11（2）：51-58.（in Chinese）

［13］王林祥，武际可.集中载荷作用下弹性球壳大范围非线性问题［J］.力学学报，1997，29（2）：232-235.WANG L X，WU J K.Large-scale nonlinear problem of elastic spherical shells subjected to concentrated load［J］.Acta Mechanica Sinica，1997，29（2）：232-235.（in Chinese）

［14］YODER Jr P R.Opto-Mechanical Systems Design［M］.3rd ed.Bellingham：SPIE PRESS，2006.

［15］DOYLE K B，HOFFMAN J M，GENBERG V L，et al..Stress birefringence modeling for lens design and photonics［C］.International Optical Design Conference，Tucson，Arizona，June 3，2002.

［16］DOYLE K B，GENBERG V L，MICHELS G J.Numerical methods to compute optical errors due to stress birefringence［J］.SPIE，2002，4769：34-42.

Design and analysis of compensation of large aperture optical element for gravity deformation

WANG Ru-dong，WANG Ping，TIAN Wei，WANG Li-peng，SUI Yong-xin，YANG Huai-jiang

（State Key Laboratory of Applied Optics，Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun 130033，China）

According to elastic shell theory，several kinds of theoretical models of large aperture optical elements were established.A compensation method for the gravity deformation from a large aperture optical element was presented.With the method，the torque was applied at the edge of a lens frame to generate flexible deformation to offset the gravity deformation.An analysis model of the large aperture optical element with the frame was proposed，and it proves that the flexible deformation of optical element can effectively eliminate the influence of gravity deformation on the optical cell through optimizing the magnitude of force and the positions of support points.

gravity deformation；flexible compensation；shell theory；finite element method

国家重大专项基金资助项目（No.2009ZX02205）

TH703

A

1674-2915（2011）03-0259-05

2011-01-11；

2011-03-13

王汝冬（1982—），男，江苏徐州人，硕士，研究实习员，主要从事光机结构设计方面的研究。

E-mail：rudong1415@163.com

隋永新（1970—），男，吉林长春人，博士，研究员，主要从事超高精密光学元件检测、光学信息融合等方面的研究。E-mail：suiyx@sklao.ac.cn