基于交比不变性约束的快速随机抽样一致性算法
王 萍,曹 楠,操晓春,欧阳健飞
(1. 天津大学理学院,天津 300072;2. 天津大学计算机科学与技术学院,天津 300072;3. 天津大学精密测试技术及仪器国家重点实验室,天津 300072)
在多种鲁棒性估计算法中,标准随机抽样一致性(RANSAC)算法[1]凭借其强大的噪声处理能力脱颖而出.然而,随着模型估计要求的提高,标准RANSAC算法的不足之处也日益彰显出来[2-5].其中,效率低是其最为突出的一个缺点[6-7].在模型估计过程中,算法采用随机取样策略,通过迭代估计模型[8].这种全局撒网式的搜索方法,随着数据中外点比例的增加,势必造成迭代次数的激增,从而影响算法效率.如果能在初始取样时直接筛选出可能的内点,就会缩小搜索范围,减少不必要的计算过程,从而提高RANSAC算法的效率.基于此想法,笔者提出了一种基于模型约束的改进算法,即利用射影变换下共线4点的交比不变性,处理高噪声数据下的平面单应矩阵估计问题.
1 概率统计分析
Guo等[9]提出,模型性质可以用来约束有效采样策略,解决大量外点存在情况下的模型估计问题.
令 Zl是由Z中元素组成的l元组的子集,对于每个 zl∈Zl,Izl代表全为内点的l点组,Ozl代表至少有1个点是外点的l点组.定义 Zl上的性质Q,且有
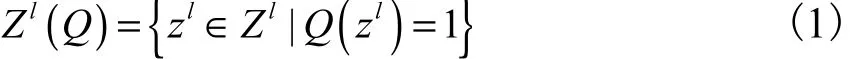
在 s个点组成的随机样本中,P ( Isl)为随机选取到l点组是内点的概率,由贝叶斯定理可知,
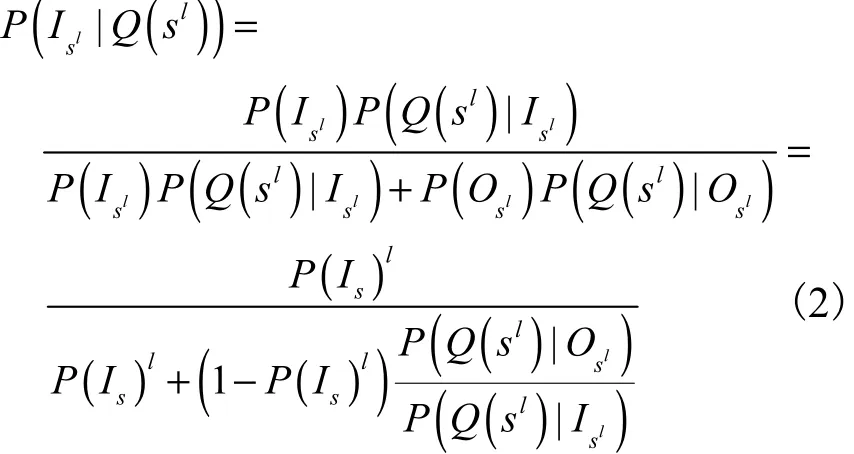
设m是估计模型所需要的最少元素个数,ρ代表在随机样本中多次采样至少1次没有外点的概率,通常取为0.99,P ( Is)为随机选取到内点的概率,则在标准RANSAC下迭代次数为
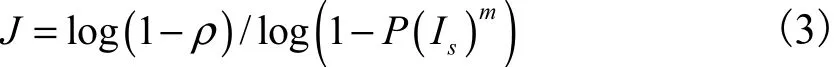
而改进后的算法估计模型所需要的最少迭代次数为
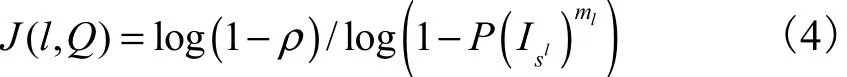
式中 ml是估计l点组模型所需要的最少元素个数.要提高改进算法的效率,就要减少不必要的迭代次数.令(,)J l QJ<,由式(3)、式(4)可知,有

与式(2)比较,可得

由此可知,要找到好的模型约束,就要满足上述的概率条件.在这种模型约束思想的引导下,笔者提出了利用射影变换下共线 4点的交比不变性提高单应矩阵估计效率的方法.
2 算法模型的建立

式中 P ( Q ( f ) |Of)代表外点中存在共线且保持交比性质的 4点组的概率.显然,这个概率可以通过估计平面上任意 4点共线且满足某一交比的概率近似得到.下面分2步求得这个概率.
2.1 计算平面上任意4点共线的概率
即使是满足约束的内点,由于噪声等影响,也不可能精确共线.Guo等[9]给出了平面上任意3点共线的概率的模型和计算方法,在此基础上,提出计算平面上任意4点共线的概率.具体模型如图1所示.设距离最远的2点为B和H,剩下的2点必然在ABH区域内(由对称性可将 BH左侧的点翻转到 ABH区域内);否则超出这个范围,BH距离就不是最远的.根据文献[9]定义距离阈值 γ,则另外两点到 BH的最短距离至少是

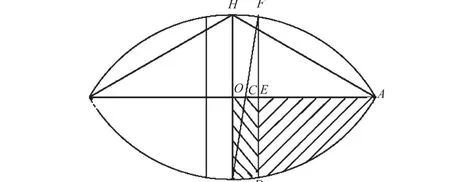
图1 4点共线约束模型Fig.1 Model using for the constraint of four points being collinear
令OE h= ,过 E点做平行于 BH的直线,当另外2点在围成的区域BHFD内时,4点近似共线.由此,根据图1,平面上任意4点共线比例可以估计为

式中S代表区域的面积.由于经过射影变换后,4个点的相对位置要保持不变,所以所求概率为
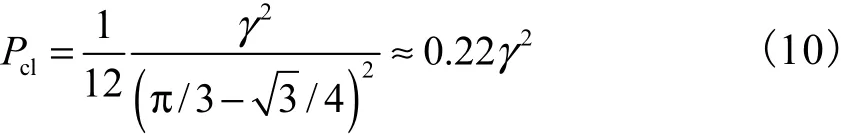
2.2 计算共线4点满足某一交比的概率

首先,确定最远的2点 p1和 p4,连接2点得到线段L,根据定义,p2和 p3在 p1和 p4之间的直线L上.在确定 p3的位置之前,p2可以在L上除了 p1和p4的任意位置.由于直线L满足均匀分布,因此,可以得到 p2定位的概率是 1.一旦确定了 p2的位置,为了满足交比k,p3的定位就不再是任意的.设 p1、p2、 p3、 p4的坐标分别为0、x2、x3、1,则交比为

由式(11),可以得出3p的位置为

故2p的坐标2x和K确定后,3p的定位概率为

这样,可以得到最后只依赖于阈值γ和δ的 4点共线且满足某一交比的概率为

将式(16)代入式(7)中,有
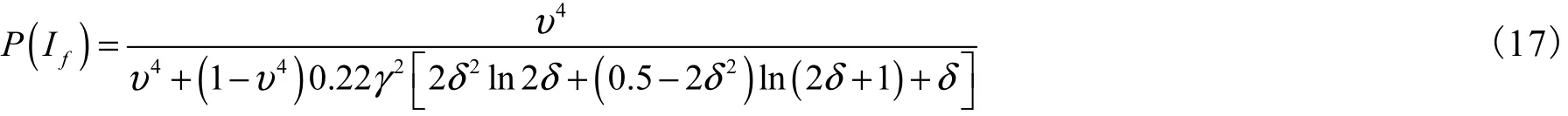
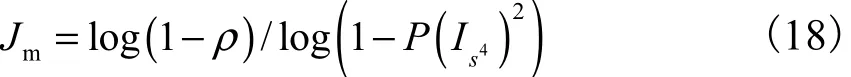

这些满足约束的点最终构成了 1个子集,这个子集中的每个元素都是由共线且满足某一交比的 4点组成.要估计1个单应矩阵,则至少需要2组这样的 4点组,即 8对点进行计算.由式(4)可知,改进后算法的最少迭代次数为因此,只要选择合适的阈值γ和δ,这种模型约束的采样方法就可以有效提高算法的迭代速度.例如,当γ和δ分别取0.06和0.09时,要想提高算法效率只需要υ>0.01,也就是说,只要数据中的外点比例不大于99%,改进的算法就比标准RASAC算法更有效率.
3 实验结果对比和分析
为了进一步证明改进算法的正确性与高效性,本节用一些实验结果来验证上述的一些结论.
3.1 验证改进算法的正确性
在第2节中计算了平面上任意4点共线且满足某一交比的概率,但这些理论值是否与实际情况相符,还需进一步验证.图2是用训练数据模拟的4点共线和共线 4点满足某一交比的验证结果,其中图2(a)为 4点共线的验证结果,可以看出,实际值保持在理论值上下波动,阈值γ的值越小,拟合效果越好;图2(b)则为共线4点满足某一交比的验证结果.
由图 2可知,实际值与理论值十分接近,它们之间的误差可近似认为是鲁棒的.
3.2 验证改进算法的高效性
当ρ= 0 .999时,取γ和δ分别为 0.04和 0.09,在不同噪声的训练数据下,比较 RANSAC、CONSAC[9]和本文改进算法的迭代次数,如表1所示.
从表1可以看出,当内点比例为1.5%时,CONSAC算法的效率比标准RANSAC算法低,也就是说CONSAC算法在外点比例大于98.5%的情况下不再有效率.而本文提出的改进算法相对 CONSAC而言,在解决高噪声数据方面的优势更加明显.
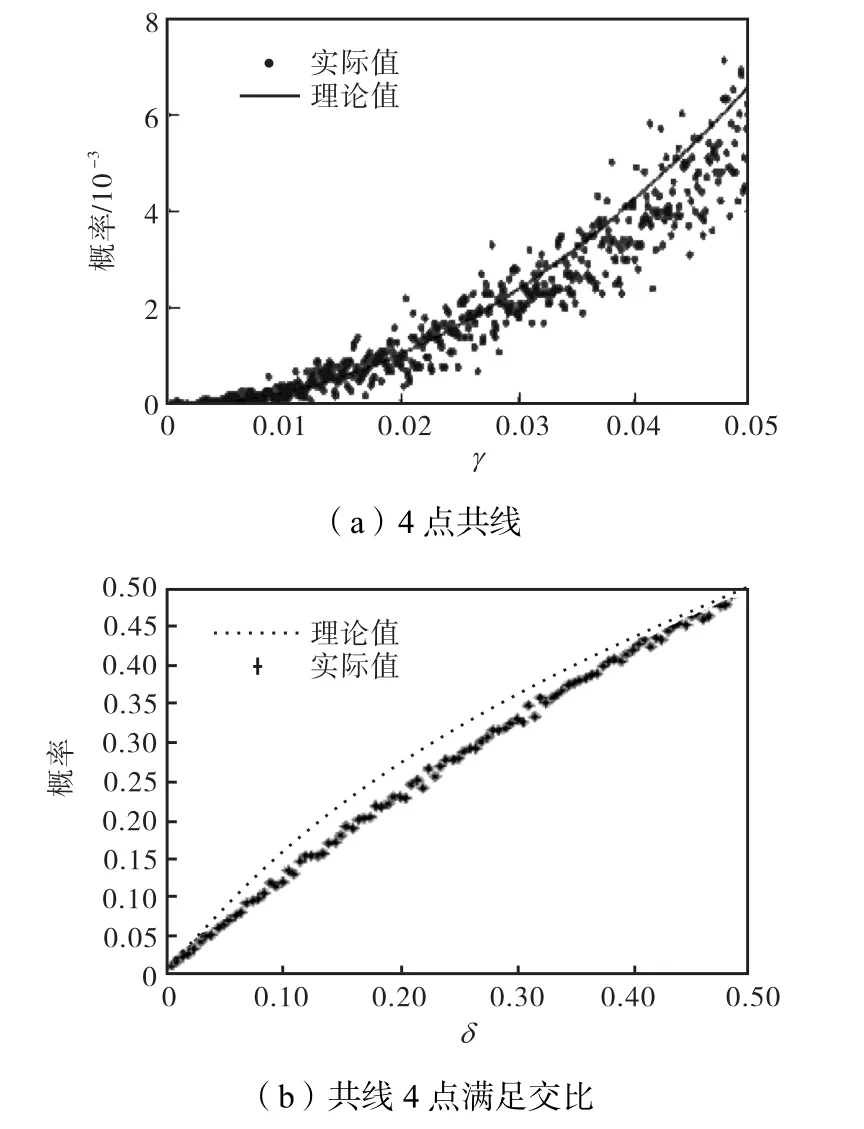
图2 4点共线与共线4点满足交比概率的理论值与实际值的比较Fig.2 Comparison between theoretical and practical probability of four points being collinear and four collinear points satisfied certain cross ratio

表1 3种算法的理论迭代次数的比较Tab.1 Comparison of theoretical iteration number among three distinct algorithms
为了使对比更加直观,将3种算法迭代次数的比较以坐标图的形式给出.如图 3所示,横坐标代表不同的内点比例;由于随着训练数据中内点比例的变化,迭代次数变化很大,这里将迭代次数取以10为底的对数作为纵坐标.图3中的3条连线,自上而下分别代表标准 RANSAC、CONSAC和本文提出的改进算法在不同内点比例情况下迭代次数的变化.
由图3可知,本文提出的算法在很大程度上减少了RANSAC算法的迭代次数,在CONSAC算法的基础上,进一步提高了处理高噪声数据的能力与效率.
4 算法应用
RANSAC估计单应矩阵在计算机视觉和图像处理方面有许多用途,如图像拼接、图像融合和纹理渲染等,这里以图像拼接为例介绍本文改进算法的应用.
图像拼接是计算机视觉领域的一个重要分支,它是将两幅以上具有部分重叠的图像进行拼接,从而得到较高分辨率或宽视角图像的一种技术[10].这里给出图像拼接的系统框架,如图4所示.

图4 图像拼接的系统框架Fig.4 Frame diagram of image stitching
图像拼接过程包括如下4个步骤.
(1) 输入两幅图像,如图5所示.
为了体现本文改进算法对高噪声数据的处理能力,尽量选择干扰大的图像,如图5的两幅图像,楼前面的树枝就是噪声,在提取特征点后,很容易将楼的特征点误匹配到树枝上,而本文算法在处理这些干扰方面是有效率的.
(2) 应用 SIFT等特征提取算法,分别提取两幅图像的特征点并匹配.
(3) 应用本文的改进 RANSAC算法,消除高噪声数据下的误匹配对,计算单应矩阵.
(4) 实现最终图像转换与拼接,如图6所示.

图5 输入图像Fig.5 Input images

图6 两幅图像拼接的结果Fig.6 Result of image stitching
RANSAC算法在拼接过程中的作用主要有 2点:一是在提取并匹配特征点后,消除其中的误匹配对,即算法中剔除外点的过程;二是计算出两幅图像之间的单应矩阵,对相应图像进行变换.而本文对RANSAC算法的改进,增强了算法处理高噪声图像的能力和速度,进一步提高了RANSAC算法的效率.
5 结 语
本文提出了一种基于采样的模型约束方法,在使用 RANSAC估计单应矩阵时,利用射影变换下共线4点的交比不变性,提前筛选出可能的内点,并使用这些候选点而不是全部的数据点进行迭代计算,很大程度上减少了迭代次数,从而提高了算法的效率.
除了理论分析,本文还选取了一系列训练数据,对算法改进的关键部分进行验证,以理论和实际结果来验证改进算法的正确性.同时,选取适当的阈值,使改进算法在处理外点比例不大于99%的高噪声数据时,比标准RANSAC算法和CONSAC算法效率更高.
[1]Fischler M A,Bolles R C. Random sample consensus:A paradigm for model fitting with applications to image analysis and automated cartography[C]//European Conference on Computer Vision. Cambridge,UK,1996:683-695.
[2]Matas J,Chum O. Randomized RANSAC with Td,dtest[J].Image and Vision Computing,2004,22(10):837-842.
[3]Chum O,Matas J. Optimal randomized RANSAC[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2008,30(8):1472-1482.
[4]Tordoff B,Murray D W. Guided sampling and consensus for motion estimation[C]//European Conference on Computer Vision.Copenhagen,Denmark,2002:82-98.
[5]Nister D. Preemptive RANSAC for live structure and motion estimation[C]//International Conference on Computer Vision.Beijing,China,2003:199-206.
[6]Zhang W,Kosecka J. A new inlier identification procedure for robust estimation problems[C]//Robotics:Science and Systems Conference.Philadelphia,USA,2006:137-144.
[7]Raguram R,Frahm J,Pollefeys M. A comparative analysis of RANSAC techniques leading to adaptive real-time random sample consensus[C]//European Conference on Computer Vision. France,2008:500-513.
[8]Hartley R I,Zisserman A.Multiple View Geometry in Computer Vision[M]. Cambridge:Cambridge University Press,2000.
[9]Guo Feng,Aggarwal Gaurav,Shaque Khurram,et al. An efficient data driven algorithm for multi-sensor alignment[C]//ECCV Workshop on Multi Camera and Multi-Modal Sensor Fusion Algorithms and Applications.France,2008:Inria-00326738.
[10]Brown M,Lowe D G. Automatic panoramic image stitching using invariant features[J].International Journal of Computer Vision,2007,74(1):59-73.

