宽叠合梁斜拉桥屈曲稳定分析

李海泉，王存国

(中铁第四勘察设计院集团有限公司 桥梁处，武汉 430063)

结构失稳是指结构在外力增大到某一量值时，稳定的平衡状态开始丧失，稍有扰动，结构变形迅速增大，使结构失去正常工作能力的现象。稳定问题可以分为第一类稳定问题和第二类稳定问题。第一类稳定问题也叫平衡分支问题，即结构达到临界荷载时，除了原来的平衡状态理论上仍然可能外，还会出现另外的平衡状态。第二类稳定问题是结构保持一个平衡状态，随着荷载的增加，在应力比较大的区域出现塑性变形，结构的变形很快增大;当荷载达到一定数值时，即使不再增加，结构变形也会迅速增加从而导致结构破坏。第二类稳定问题实际上是极限荷载的问题。实际的结构中，所有的稳定问题都是第二类稳定问题。只不过由于第一类稳定问题的力学概念比较明确，在数学上可归结为特征值问题，求解相对较容易，而它的临界荷载又近似地代表着第二类稳定的上限，所以在理论分析中占有重要地位，许多规范都是以第一类弹性稳定问题的表达式作为基础，验算结构的稳定性。我国斜拉桥规范中即参考拱桥规定结构弹性稳定安全系数须 ＞4。

求解结构稳定问题的实质是求结构在给定荷载作用下的一种临界状态，确定临界荷载和相应的屈曲形态。在一定变形状态下的结构静力平衡方程式可写成如下形式

式中，［Ke］为结构弹性刚度矩阵;［Kσ］为结构几何刚度矩阵;{u}为结构整体位移向量;{p}为结构外力向量。

在进行线弹性屈曲分析时，［Kσ］与{p}同比例增长。故式(1)可写成如下形式

由第一类稳定问题的定义可知，当结构处在临界状态下，其平衡方程式(2)必有特殊解，条件是系数矩阵的行列式为零，即

式(3)在数学上是一个广义的特征值问题，称λ为特征值，相应的{u}为特征向量，它表示结构的屈曲模态。如果方程有n阶，理论上存在n个特征值，工程问题中，只有最小的特征值才有实际意义，最小的特征值即为结构的稳定安全系数。

1 工程概况

宁波绕城公路甬江特大桥为联塔四索面分幅钢混凝土双Π形叠合梁斜拉桥，跨径为54 m+166 m+468 m+166 m+54 m，如图1所示。索塔采用 C50混凝土索塔，钻石型结构，总高141.5 m，索塔上塔柱在其顶部区域通过混凝土板相联(称为塔柱结合部)。甬江特大桥标准段边主梁高2.3 m，桥面板厚27 cm，见图2。斜拉索采用平行钢丝斜拉索，各索塔的中跨、边跨各设18对斜拉索，全桥共288根斜拉索;拉索在主梁上的基本索距为12 m，在索塔上基本索距为2.042～4.585 m，属于现代密索体系斜拉桥。桥梁设计荷载等级为公路Ⅰ级，桥面宽52.1 m，整个梁体在墩顶设竖向和横向支承，是半漂浮体系结构。该桥建成后将成为世界上最大跨度的双塔四索面斜拉桥。

2 全桥有限元模型

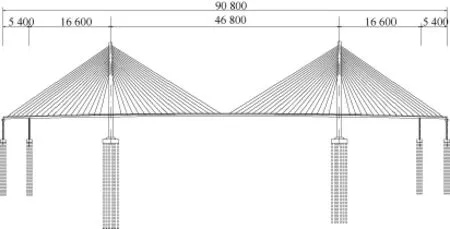
图1 总体布置(单位:cm)

图2 主梁标准横截面示意(单位:mm)

采用有限元软件ANSYS进行建模，主梁和索塔采用beam 188单元模拟，辅助墩采用beam 4模拟，索塔横梁和主梁临时固结采用刚臂单元MPC 184连接，全桥模型共有20 775个节点，2 185个单元。材料参数取值如下:主梁为C50混凝土，弹性模量3.45×104MPa，泊松比0.2，密度2 600 kg/m3;主墩为C55混凝土，弹性模量 3.55×104MPa，泊松比 0.2，密度 2 600 kg/m3;承台为C30混凝土，弹性模量3.0×104MPa，泊松比0.2，密度2 500 kg/m3;桩基础为C40混凝土，弹性模量3.25×104MPa，泊松比 0.2，密度为 2 550 kg/m3。

边界条件为:台座底完全固结，边墩与辅助墩墩底完全固结，边墩及辅助墩与主梁的连接采用约束相应自由度来实现。全桥有限元模型共有2 648个节点，1 892个单元。局部消隐图见图3、图4。

图3 塔梁结合处局部消隐图

图4 边跨支座处局部消隐图

3 稳定性分析

3.1 裸塔状态的稳定

裸塔状态时，台座底固结。考虑恒载 +横风(20年一遇)。稳定计算结果见表1，图5。

表1 裸塔阶段稳定计算结果

图5 裸塔阶段失稳模态

由于只有一阶失稳才有意义，因此仅给出该阶段的一阶失稳模态，以下其它状态(阶段)亦如此。

3.2 最大双悬臂状态的稳定

最大双悬臂状态时，梁塔临时固结。稳定分析时，考虑恒载(包括施工挂篮等)+横风(20年一遇)+横风引起的不平衡升举力。稳定计算结果见表2，图6。

表2 最大双悬臂阶段稳定计算结果

图6 最大双悬臂阶段失稳模态

由分析可知，该斜拉桥在最大双悬臂状态有较高的稳定安全系数。

3.3 最大单悬臂状态的稳定

最大单悬臂状态时，梁塔临时固结。稳定分析时，考虑恒载(包括施工挂篮等)+横风(20年一遇)+横风引起的不平衡升举力。稳定计算结果见表3，图7。

表3 最大单悬臂阶段稳定计算结果

图7 最大单悬臂阶段失稳模态

通过分析可知，前4阶失稳模态均属于面内失稳，主要为主梁失稳。

3.4 成桥状态的稳定

成桥状态的稳定分析时，考虑恒载+100年一遇横风的作用。稳定计算结果见表4，图8。

表4 成桥阶段稳定计算结果

图8 成桥阶段失稳模态

由分析可知，该阶段均为面内失稳，主要为主梁失稳，有较高的稳定安全系数。

4 结论

1)各计算工况的弹性稳定安全系数全部 ＞4，满足规范要求，由此可见甬江特大桥在施工和运营阶段的弹性稳定满足要求。

2)从各施工阶段的失稳模态可以看出，索塔刚度较大，主梁在压应力作用下更容易失稳。

3)对于大跨径斜拉桥，将弹性整体屈曲力作为判断桥梁是否满足要求的最终标准是偏危险的，因此有必要进行非线性分析综合考虑。

4)通过计算机模拟，工程技术人员可以事先了解到可能出现的问题，通过优化施工方案，加强施工监控，使施工风险降到最小。

［1］陈勋.万州长江二桥桥塔稳定分析［J］.铁道建筑，2007(12):4-6.

［2］向中富，顾安邦.大跨径斜拉桥稳定分析［C］∥桥梁学术论文集.北京:人民交通出版社，2000.

［3］李国豪.桥梁结构稳定与振动［M］.北京:中国铁道出版社，1996.

［4］刘兆丰.大跨度联塔分幅斜拉桥结构行为与联塔结构模型试验研究［D］.成都:西南交通大学，2009.

［5］肖光宏，张秋陵，黄明海.几何非线性对大跨斜拉桥稳定性的影响［J］.重庆交通学院学报，2007，26(3):17-19，32.