铁路钢筋混凝土连续梁桥静力弹塑性抗震分析

杨智玲

(沈阳铁道勘察设计院有限公司，沈阳 110013)

我国是一个多地震的国家，铁路桥梁作为生命线工程重要组成部分，其抗震性能好坏对于震后救援工作具有非常重要的意义。大地震发生时，结构不可避免地进入弹塑性工作阶段，弹性反应谱分析无法直接反映结构的一些非线性特性。近些年来，静力弹塑性分析作为一种简单而有效的抗震评估方法，在建筑结构抗震设计评估中得到了广泛应用，但在我国尚未应用于桥梁结构设计分析。本文以某铁路钢筋混凝土连续梁桥为例，对该桥进行静力弹塑性抗震计算，并与弹性反应谱分析结果对比，对相关问题加以探讨。

1 计算模型的建立

1.1 桥梁概况

该桥全联长176 m，跨径布置为(48+80+48)m预应力混凝土连续箱梁。上部结构为单箱单室单线箱梁，混凝土采用 C50。主梁顶板宽 7.2 m，底板宽4.2 m，墩顶部位梁高5.8 m，跨中部位梁高3.0 m，箱梁梁底采用1.6次曲线变化。桥墩高16 m，采用矩形实体桥墩，界面尺寸为4 m×6 m。桥墩混凝土采用C30，配筋主筋采用HRB400，直径32 mm双层布筋，箍筋采用HRB335，直径16 mm，间距0.1 m。墩底采用12根直径3 m的挖孔灌注桩基础。

1.2 有限元模型

通过有限元方法对桥梁结构进行动力分析，首先需要建立合理的计算模型。包括上部结构和下部结构单元的选取和离散划分、支承部位的模拟、墩台边界的处理以及荷载的确定。本文基于大型有限元软件MIDAS Civil 2010，建立全桥模型。其中主梁和桥墩采用空间梁单元模拟，支座采用线性弹簧单元模拟。考虑了桩土的相互作用，采用6根弹簧表示墩底的约束条件。全桥有限元模型如图1所示。

图1 有限元计算模型

2 模态与反应谱分析

2.1 模态分析

结构自振特性决定结构的动力响应，同时也是反应谱计算的基础。常规模态分析为线性的，结构自振特性主要与结构刚度与质量的分布有关。基于前述模型，综合考虑该桥的空间特性，将结构自重与二期恒载转换为质量。特征向量采用 Lanczos方法求解，计算阶数为前100阶，表1列出该桥前10阶自振特性。

从上述分析结果可知，全桥第一阶振型为全桥纵飘，且振型质量贡献率达到86.97%，该振型对纵桥向影响较大。

2.2 反应谱分析

基于设计资料，桥位处地震烈度为Ⅷ度，按照Ⅸ度设防。场地土类型为中硬土，场地类别为Ⅱ类场地，特征周期为0.35 s。基于《铁路工程抗震设计规范》GB50111—2006(2009版)，考虑多遇地震和罕遇地震两种地震烈度情形，其基本水平地震加速度分别为0.14 g和0.64 g，反应谱图形如图2所示。计算中振型的组合方式采用CQC组合。

表1 结构自振特性(前10阶)

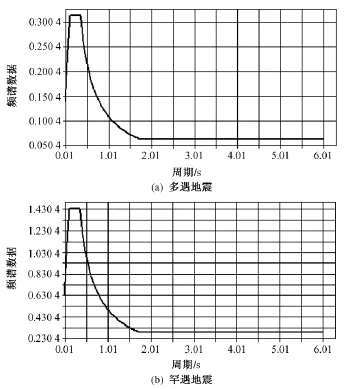
图2 地震反应谱

由弹性反应谱分析可知，多遇地震作用下，在纵向地震工况下墩顶最大纵向位移为0.013 m，横向地震工况下墩顶最大横向位移0.007 m;罕遇地震作用下，在纵向地震工况下墩顶最大纵向位移为0.057 m，横向地震工况下墩顶最大横向位移0.033 m。

3 静力弹塑性分析

3.1 弹塑性模型的建立

以往震害资料表明，绝大多数桥梁震害主要源于下部结构的破坏，因此本文重点关注地震作用下桥梁墩柱的非线性行为。在弹塑性地震反应分析中，桥墩的恢复力模型确定是最基本的一环。使用有限元软件MIDAS Civil 2010对桥墩模拟时，需要输入模拟塑性铰的非线性单元骨架曲线参数。本文采用弯矩—曲率关系定义的非线性分布式铰模型，同时考虑轴力—弯矩交互影响，采用多轴铰本构P—M—M模型。

首先通过Imbsen Software公司开发的专业软件XTRACT对桥墩截面进行了弯矩—曲率分析和轴力—弯矩相互作用分析。在上部结构自重作用下，桥墩截面的轴力—弯矩相互作用如图3所示，图中拟合计算结果与美国ACI规范折减计算结果相同。

图3 桥墩截面的轴力—弯矩相互作用

由上述相互关系可以确定出构件屈服面，通过轴力来计算屈服弯矩。将相关参数输入MIDAS Civil 2010，两个方向的弯矩和屈服弯矩满足Bresler公式

式中，Mnx，Mny为截面 x，y方向的弯矩值;Mmax为给定轴力作用下的屈服弯矩;α决定曲面形状，折线形取1，椭圆形取2。

在静力弹塑性分析中，侧向加载模式较为关键。考虑到桥墩构件沿高度方向分布较为均匀，且底部最为薄弱，本文采用加速度常量加载模式，将荷载以惯性力的形式分布作用于结构。侧向力按照纵桥向和横桥向两种工况分别施加，采用位移控制法，每种工况计算步骤数为100，同时分析中考虑了P-delta效应。

3.2 能力谱分析

能力谱方法是静力弹塑性分析中较常采用的方法，其基本思想是建立两条相同基准的谱线:一条是由荷载—位移曲线转化的能力谱曲线，另一条是由加速度反应谱转化的ADRS谱(亦称需求谱曲线)，将两条线放在同一个图中，两曲线的交点定义为目标性能点，依此判断结构抗震性能。

由于我国桥梁规范缺乏相关的规定，参考美国ATC-40推荐方法，同时参照《铁路工程抗震设计规范》规定反应谱求取目标性能点，基本流程如下:

1)首先由静力弹塑性分析求得基底剪力和墩顶位移的关系曲线;

2)将Pushover分析曲线转化为能力谱;

3)依据规范规定的反应谱建立弹性需求谱，将能力谱与弹性需求谱绘制在同一图中，获知初始性能点;

4)计算性能点上的等效阻尼及有效阻尼，利用有效阻尼建立弹塑性需求谱，并获得弹塑性需求谱与能力谱，即新的性能点;

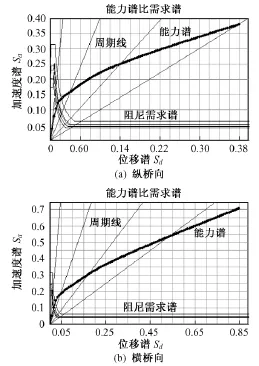
图4 Ⅸ度多遇地震下桥墩能力曲线

在多遇地震下，纵桥向性能点为 Sa=0.122 6，Sd=0.015 5，经转化公式得墩底剪力为 Vb=5 927 kN，墩顶位移 u=0.012 m;横桥向性能点为 Sa=0.124 8，Sd=0.021 6，经转化公式得墩底剪力为 Vb=4 567 kN，墩顶位移u=0.007 m。结构达到性能点状态时桥墩构件尚在弹性范围内。

在罕遇地震下，纵桥向性能点为 Sa=0.225 5，Sd=0.105 6，经转化公式得墩底剪力为 Vb=10 900 kN，墩顶位移 u=0.083 m;横桥向性能点为Sa=0.242 1，Sd=0.104，经转化公式得墩底剪力为Vb=8 858 kN，墩顶位移 u=0.037 m。结构达到性能点状态时桥墩墩底进入塑性状态。从墩顶纵横向位移反应来看，在罕遇地震下纵桥向弹塑性位移较弹性反应谱分析结果大45.61%，横桥向弹塑性位移较弹性反应谱分析结果大12.1%。

总之，能力谱曲线与需求谱曲线均产生交点，说明该桥满足Ⅸ度罕遇地震下结构抗倒塌要求。

5)重复以上过程，直至性能点上的位移与加速度响应满足允许误差。

基于上述流程，本文计算了该桥在多遇地震和罕遇地震作用下纵桥向与横桥向桥梁响应。经过Pushover分析将能力曲线、需求曲线以及反应谱曲线按照A-D格式画在同一张图中，如图4与图5所示。

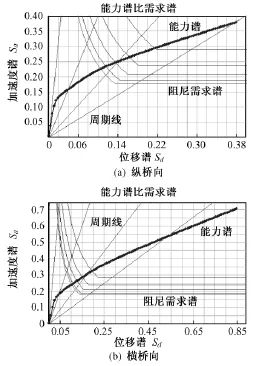
图5 Ⅸ度罕遇地震下桥墩能力曲线

4 结语

静力弹塑性分析方法是近年来发展较快的抗震性能评估方法，该方法既能对结构在多遇地震下的弹性设计进行校核，也能确定结构在罕遇地震下潜在的破坏机制，从中找出相对薄弱环节，设计者可以依此局部加强或修复。

［1］中华人民共和国铁道部.GB50111—2006 铁路工程抗震设计规范［S］.北京:中国铁道出版社，2009.

［2］卓卫东.桥梁延性抗震设计［M］.北京:人民交通出版社，2001.

［3］王克海.桥梁抗震研究［M］.北京:中国铁道出版社，2007.

［4］北京金土木软件技术有限公司.Pushover分析在建筑工程抗震设计中的应用［M］.北京:中国建筑工业出版社，2010.

［5］邱顺东.桥梁工程软件 MIDAS Civil常见问题解答［M］.北京:人民交通出版社，2009.