基于逐步回归分析的大坝变形分析模型研究

张洁洁,陈天伟,陈凯华

(桂林理工大学土木与建筑学院测绘工程系,广西桂林541004)

0 引 言

我国水资源贫乏,但是我们水能资源却十分丰富,为了开发利用这些水资源和水能资源,我国迄今已经修建了约8.4万座堤坝,是世界上建坝最多的国家,这些水利工程在防洪、灌溉或供水、发电和航运等方面产生了巨大的社会经济效益。

但同时据水利部和国家电力公司对所属大坝的安全定期检查发现[1],大坝安全管理和安全检测的任务十分艰巨。设置安全监测系统,通过长期坚持观测和资料分析,及时对工程进行加固,以避免事故发生十分重要,因此,监测数据应得到及时的分析评价[2]。

1 逐步回归分析的基本步骤

综合筛选预报因子的统计检验和矩阵的基本运算公式[3],可将逐步回归计算的全过程分为下列基本步骤:

1)计算相关矩阵

为提高计算结果的精度,用二次均值算法代替一次均值算法,用标准化的相关矩阵rij代替Sij,扩展为(k+1)阶矩阵,y用n表示,即

标准化的法方程式:

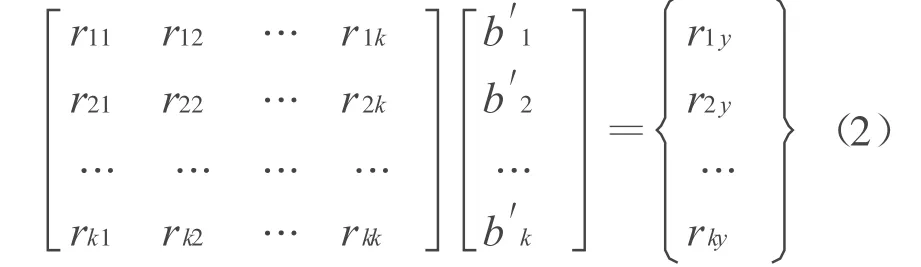
2)因子筛选和消元变换

在逐步回归分析中,第1,2步引入因子分别在因子集合¯G(0)与¯G(1)中,选择对y作用最显著的因子引入回归方程。注意:G(0)、G(1)分别表示第0步和第1步逐步回归方程中所有包含因子的集合;¯G(0)、¯G(1)分别表示第0步和第1步不在逐步回归方程中的所有包含因子的集合。从第3步开始,先剔后引,即首先剔除在当时回归方程中的不显著因子,然后引入当时回归方程以外对y作用显著的因子进入回归方程,引入和剔除因子都要进行F检验,并求出各步回归方程的回归系数、复相关系数以及剩余标准差。

经过上述变换后,引、剔因子所用特征值的计算公式:

1)偏回归平方和Q(m)j

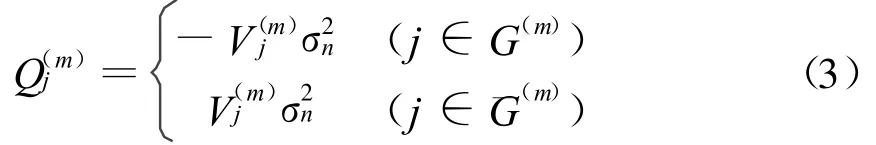
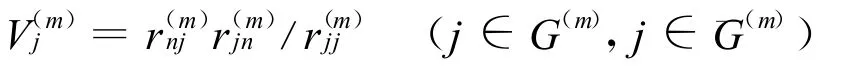
2)第m步回归方程的剩余平方和Q(m)

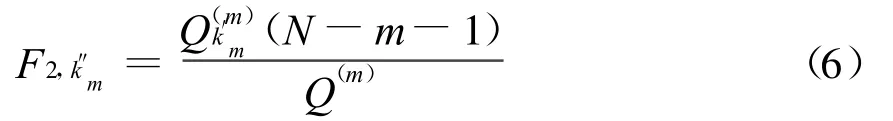
当F2,k′m≤F2时,从回归方程中剔除;F2,k′m>F2时,不剔除。

4)引入因子xkm+1的检验

在第m步回归方程以外的因子中,选择对y作用最明显的因子,即其偏回归平方和为最大的因子

当F1,km+1>F1时,接纳xkm+1因子;否则不接纳。

5)第m步的回归系数、复相关系数和剩余标准差

2 逐步回归分析的应用实例分析

宜昌市尚家河水库位于宜昌市夷陵区分乡镇境内,是黄柏河东支流域梯级开发群中的最后一级。离西北口水库坝址9 km,距宜昌市50 km,系宜昌市东风渠灌区渠首取水工程。

尚家河水库溢流坝加高工程于2002年元月15日动工,2002年3月28日竣工,2002年4月30日投入使用。2002年4月29日首次测量偏距为初始值;水平位移正负号规定:向下游为正,向上游为负,如表1所示。

图1为从2009年4月29日起的水平位移、气温以及库水位的示意图。

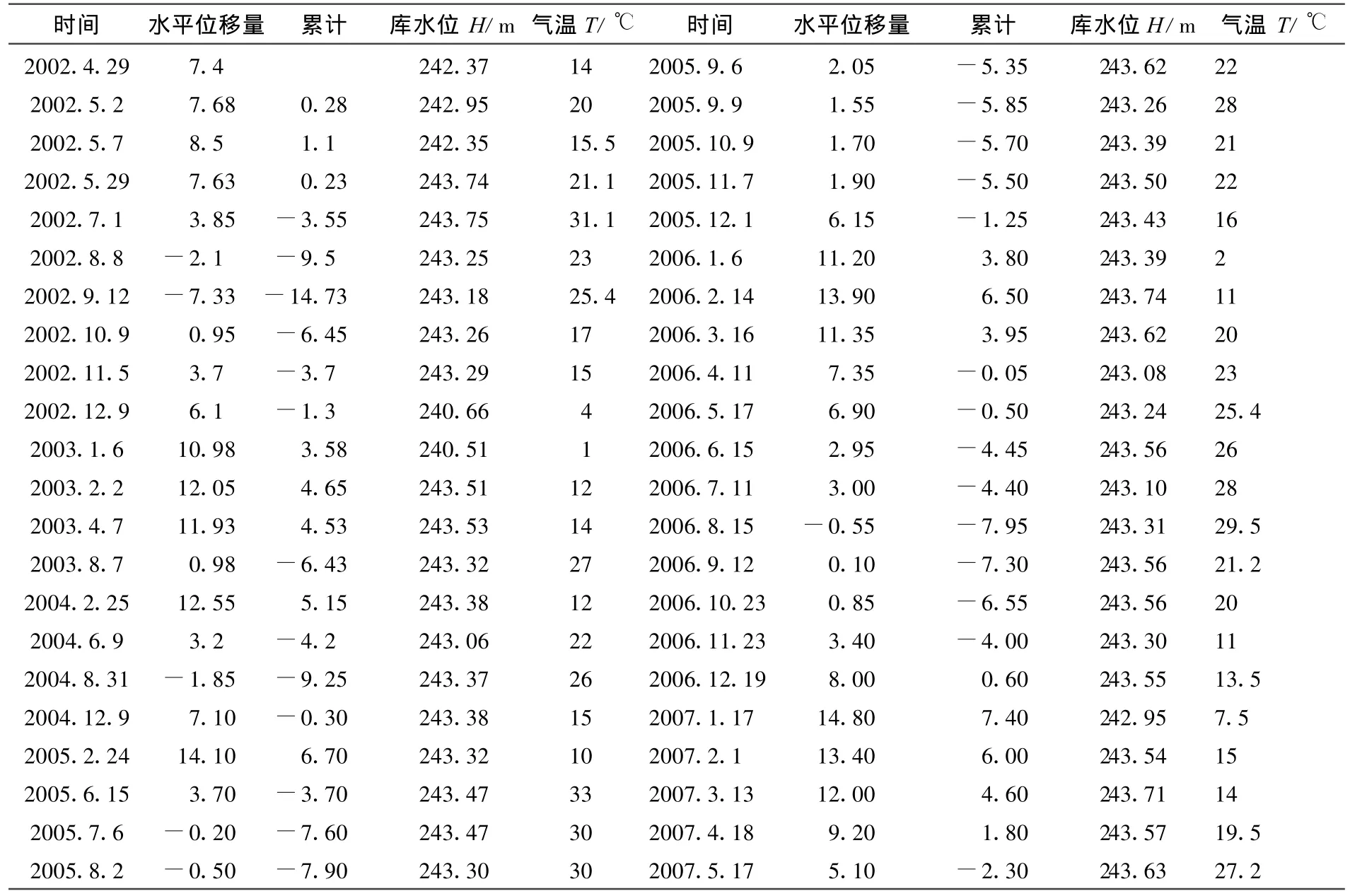
表1 尚家河水库溢流坝(水平位移量、库水位、气温)观测值

图1 2009年4月29日起的水平位移、气温以及库水位的示意图

根据此坝的外部观测资料,我们选用2002年8月8日-2007年6月21日间的观测值作为子样资料,共40组。蓄水初期的资料未采用,主要是考虑初期坝体尚有残余水化热等因素,致使其变形规律未必与以后规律一致,而对于坝的安全运行而言,更需要摸清的是近期的变化规律[4]。

引起大坝变形的因子比较多,与大坝变形有关的效应量通常分为库水位,时效和温度三个,我们选用以下因子。

1)库水位

库水位H采用当天的测值,选取 H、H2、H3为水位位移因子,即水位位移:

2)时效变形时效变形^δθ值,以月为单位。对于第一月测值 θ1=0,第二月测值θ2=1,依次类推。

3)温度T

坝内温度与气温密切相关[5],并取决于气温。因为该坝未测量坝内温度,而这部分的温度变化对坝顶水平位移有较大的印象,因此采用 T15、T30、T60、T90四个温度因子。T30是从观测日期回溯30天,并将该30天的日平均温度加以平均而得到的。

如果模型选用完全八个因子进入回归模型,建立回归模型1

由社会科学统计程序(SPSS)数理统计软件可求得回归方程为

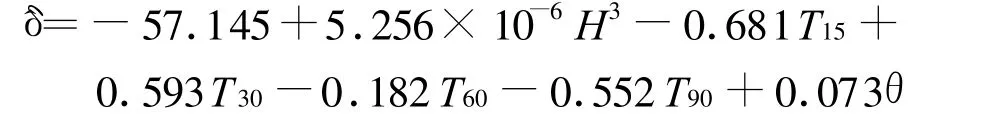
复相关系数 R=0.928,R2=0.861

标准差 Sδ=2.20435 mm

F检验 F=34.021

由此模型对观测值的预测见图2和表2。

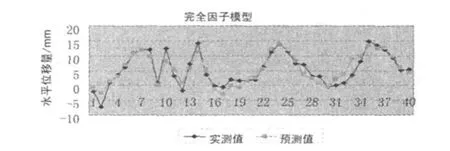
图2 完全因子模型

表2 模型1对观测值的预测

计算结果表明:

1)在40个点中,残差超过2 mm的有14个(最大为5.38934 mm)。在1～2 mm之间的有7个,其余19个小于1 mm,且正负交替,分布比较均匀。复相关系数R=0.928。由此可见,其拟合还是比较令人满意的。同时说明所选择因子的正确性。

运用逐步回归原理对上述模型依次剔除变量H3、T30、T60,得到最优回归子集模型2。

再由SPSS数理统计软件求得最优回归方程为

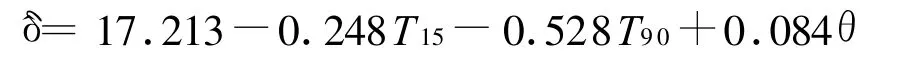
复相关系数R=0.922,复决定系数R2=0.850,而全模型的复决定系数R2=0.861。

F检验 F=67.988

用此模型预测的结果如图3和表3所示。

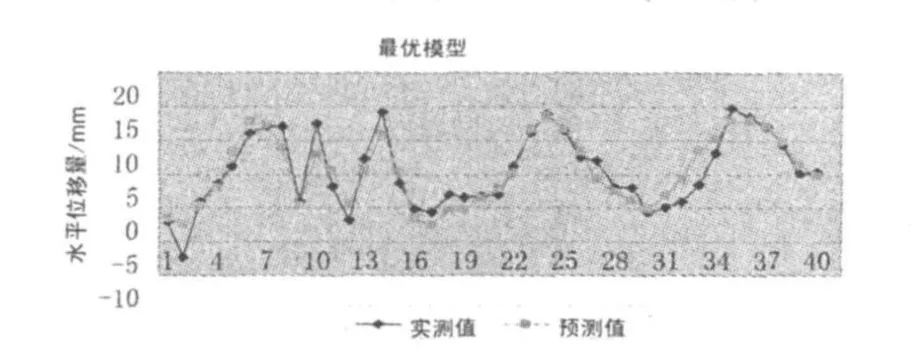
图3 最优模型

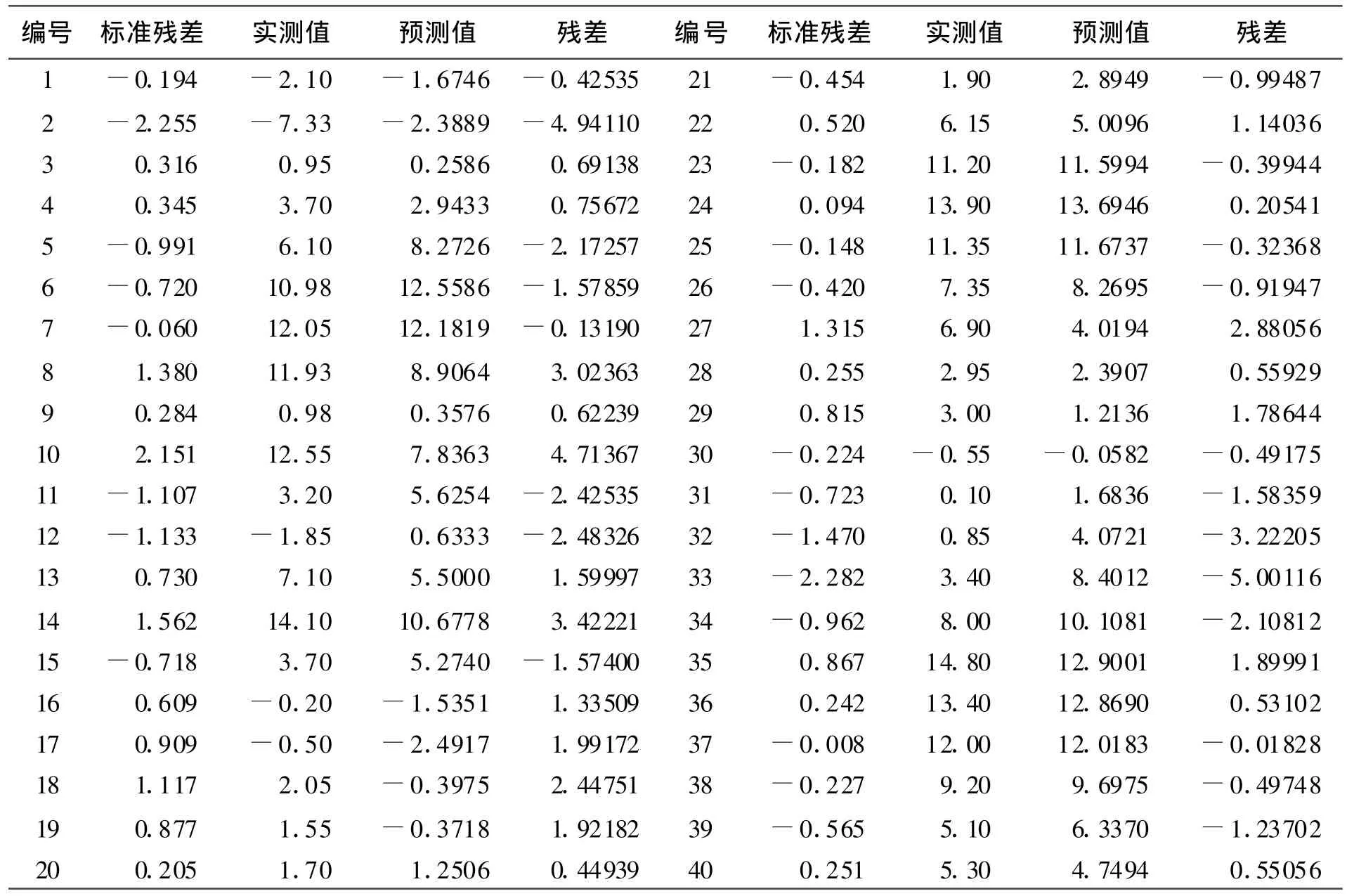
表3 模型2对观测值的预测

计算结果表明:预测值与实测值残差超过2 mm的有12个(最大为5.00116 mm)。残差在1～2 mm的有11个,其余17个都小于1 mm,且正负交替。复相关系数R=0.922,其拟合程度较好,虽然残差小于1 mm的数目比全模型要少,但在剔除三个因子之后同样达到了比较理想的预测目的,使模型更加简单[6]。

如图4所示,从残差比较可以看出最优模型要优于完全模型,但不是很明显,这可能与观测数据较少有关。总体来说,所建立的逐步回归模型是合理的[7],可以达到预测的目的。

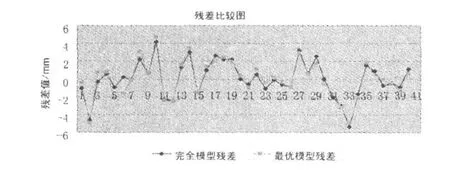
图4 残差比较图

4 结 论

引起大坝变形的因子比较多,因子的选择是回归分析中一个重要环节,大坝变形因子是结合了大坝理论力学和以往经验进行的选择。

研究发现通过对所建回归模型的分析,可以直观的看出引起大坝变形的因子在其中所起的影响程度,这样更有利于指导大坝安全检测工作,保证大坝的安全运行。但回归模型属于统计模型中的一种,很多解释都来自于数学理论和已往的监测经验[7],所以回归模型在大坝监测上面理论基础不强,不过随着科技的不断发展,确定模型与统计模型的结合将越来越成熟。

[1] 吴中如.水工建筑物安全监控理论及其应用[M].北京:高等教育出版社,2001.

[2] 方卫华.对大坝安全监测的几点认识[J].北京:大坝与安全,2004(6):26-28.

[3] 王孝仁,王松桂,编译.实用多元统计分析[M].上海科学技术出版社,1990:195-264.

[4] 陈永奇,吴子安,吴中如,等.变形监测分析与预报[M].北京:测绘出版社,1998.

[5] 徐培亮.大坝变形预测方法的扩展[J].测绘学报,1987,16(4):280-290.

[6] 邓跃进,董兆伟,张正禄.大坝变形失稳的尖点突变模型[D].武汉测绘科技大学学报,1998,24(2):170-175.

[7] 何晓群,刘文卿.应用回归分析[M].2版.北京:中国人民大学出版社,2003.