有源电力滤波器延时效应分析与补偿次数设定

董天兵,程汉湘,何满润

(广东工业大学 自动化学院,广东 广州 510006)

1 引言

有源电力滤波器(APF)是未来谐波治理的主要电力装置。有源滤波器的理论和应用研究取得了极大进展,进入工程应用攻坚阶段,有一些问题尚待解决[1],如IPM模块保护,提高补偿效果等,有源滤波器的研究工作仍在积极进行中。许多企业推出了自己的有源滤波器产品,并在技术参数中标称了“谐波补偿次数”。从理论上讲,有源电力滤波器可以补偿任意次谐波,但是由于电流互感器、开关频率和数字低通滤波等导致的一系列延时,使得APF谐波补偿次数受到限制,很少论文涉及这方面内容。现有的少数产品中,仅说明了谐波补偿次数,而未对最高补偿次数以上的高次谐波处理,对降低谐波畸变率有一定影响。本文针对APF系统延时进行建模分析,探讨了如何针对设计好的APF系统确定最高补偿次数,并通过设计安装低通滤波,使补偿效果改善,总谐波畸变率降低,从而为APF设计和工程应用提供有效的指导。

2 延时分析

APF在进行采样滤波信号处理到逆变输出过程中,由于采样间隔延时、互感器相位延迟和信号处理延时等,使得补偿电流与电网电流会有一定的相位差,会对高次谐波补偿效果造成影响,甚至放大高次谐波。以某次谐波相对于基波的百分含量来衡量,若某次谐波补偿后百分比高于补偿前的百分比,显然没必要进行补偿。这个谐波次数就是APF可以补偿的最高次数。

APF延时包括互感器延时、A/D转换延时、数字低通滤波、注入电路延时和逆变开关动作延时等[2],如图 1所示。

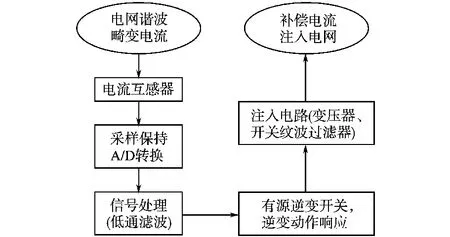
图1 有源滤波器信号处理流程图Fig.1 Signal processing flow chart of APF

根据国家电流互感器标准GB 1208-1997可知[3]:0.5级精度的电流互感器,其相位延时误差会达到 30′～ 90′,即 0.5°～ 1.5°。取其平均值1°,对应基波电流延时为

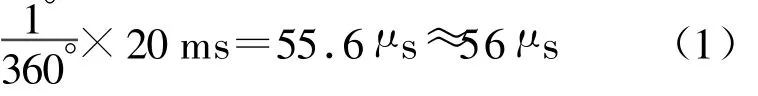
采样保持器集成在A/D转换器内部,因此可将采样保持器和A/D转换器引起的延时作为整体讨论,即数据采样延时。高速A/D转换芯片,从数据采样保持,到微处理器(以DSP为例)接收到转换结果(三相数据)只需几,选用TMS320F2812的高速集成A/D芯片数据采样引起的延时小于 10 μ s,以 10 μ s 计算 。

数字信号处理阶段引起的延时主要指微处理器完成计算任务需要的时间,选用快速DSP芯片,耗时相对来说较短。如选用 TI公司的TMS320F2812DSP快速处理芯片,每秒可执行150 M条指令(MIPS),单就谐波检测算法而言,若采用ip,iq算法计算电网谐波电流,那么从读取采样结果到发出三相PWM脉宽数据大约需要450条指令,需要3μ s的时间,如果用C语言程序效率低一点,最多也只需要10～20 μ s的时间,以20 μ s计算 。

有源逆变动作响应时间。英飞凌公司的IGBT模块FF300R17ME3,开通延时和关断延时总共不超过2 μ s,几乎可以忽略不计。

由上可知,DSP采样以及补偿指令计算时间TP≈30μ s。在10 kHz采样频率下,采样间隔时间为TS=100 μ s。(TS+TP)表示最大延迟时间,TP表示最小延迟时间,所以数字控制等效平均延迟时间[2]为

再加上电流互感器延时,注入电路延时等约为140 μ s。即从电网或者负载电流检测开始,到补偿电流注入电网,一个采样点从输入到逆变输出需要经过140 μ s(未包括低通滤波器响应时间)延时。

上述估算得到140 μ s的延时,使有源电力滤波器达不到严格意义的实时补偿,虽然延时仅为工频周期(20 ms)的 0.7%,造成 2.52°的相位延迟角。但是,这段延时对于13次(650 Hz)、19次(950 Hz)谐波相位延迟角分别为32.76°,47.88°。随着这些延时的增大,补偿谐波次数的升高,补偿效果将会变得很差,甚至起不到补偿作用,造成谐波放大[4]。

由以上分析可知,数字控制器控制信号离散化是引起数字控制器误差的主要原因,互感器采样延时也是造成补偿效果不理想的主要原因,它们可以统一看作补偿的延迟。虽然这样的延迟可以通过互感器相位补偿、提高采样频率、换用高速数字信号处理器等方法减小,但是无法避免,它必然对高次谐波的补偿带来误差。

3 建模仿真得出最高补偿次数

APF仿真系统过于复杂,多模块多参数相互影响,难以通过仿真研究单纯延时对补偿效果的影响。为此,根据APF系统延迟电流补偿,构建简易模型,来研究单纯性延时对补偿效果的影响。如图2所示,建立三相桥式不可控整流电路模型,提取其a相电流信号作为非线性负载电流,取一个与三相不可控整流负载电流基波幅值相同的正弦信号,相位角均为零;负载电流信号和正弦波信号相减,作为APF的补偿电流。补偿电流信号经过140 μ s的延时环节,与负载电流信号相加,得到补偿后的电流I。通过对补偿后的电流和负载电流信号做傅里叶分析,进行高次谐波含量对比,确定最高补偿次数和采样截止频率。Matlab仿真模型如图2所示。

利用Powergui模块对负载电流IL和I进行快速傅里叶分析,最大分析频率设置为3 000 Hz(60次谐波)。与Sine相位均为0,Delay模块中“Time delay”设定为“140e-6”。仅延时对补偿波形的影响如图3所示,13次以上典型谐波FFT分析见表1。

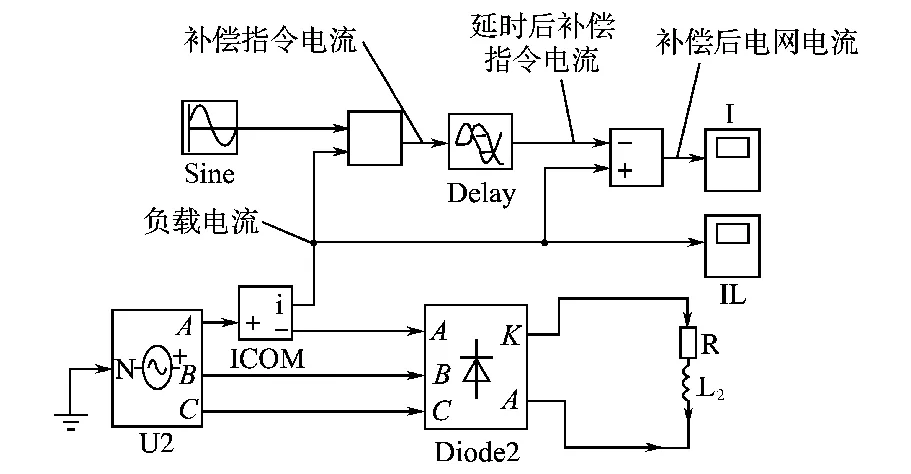
图2 APF系统延时简易模型Fig.2 Simple simulation model of APF system time delay

图3 APF延时补偿效果Fig.3 Compensation effect chart of APF time delay

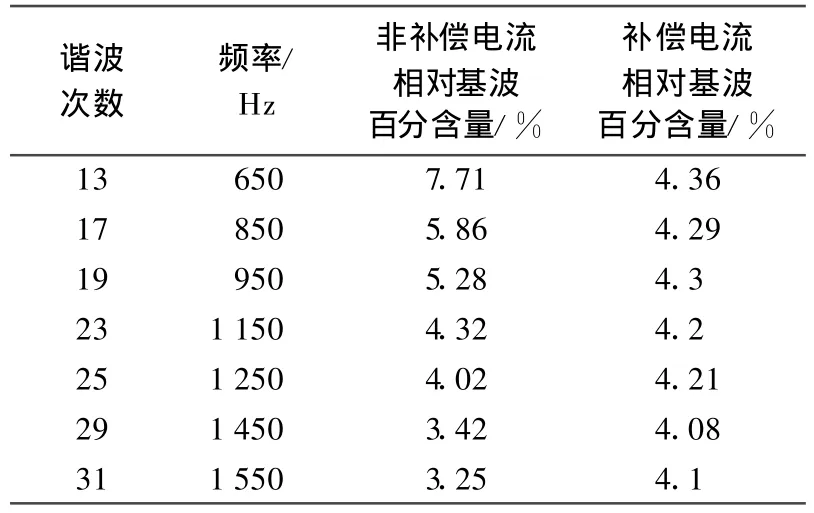
表 1 FFT分析结果(140 μ s延时)Tab.1 FFT analy sis result(140μ s time delay)

由表1可知25次以上的谐波被放大了,而且放大倍数随着谐波次数的增加而增加,在这样的系统延时条件下,最大谐波补偿次数为25次。电流总谐波畸变率补偿前后分别为30.16%,17.4%,补偿效果并不理想。不同场合的负载有不同的补偿要求,如电弧炉等非线性负载谐波频谱非常丰富,最高25次的谐波补偿和补偿后17.4%的谐波畸变率远远不能满足要求,需要设法减小延时,提高补偿次数。

电流互感器延时较大,如果换用0.2级或0.1级的电流互感器,延时误差会达到15′以下,相位延迟误差仅为0.25°,延时时间为

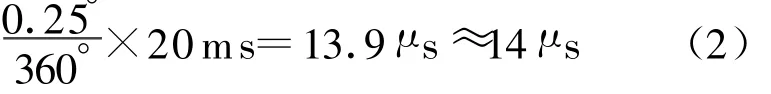
另外采样频率提高至16 kHz,TS=62.5 μ s,那么数字控制等效平均延迟时间τ=(TS+2TP)/2=61.125 μ s。这样总延时约为 75 μ s,基波对应相位延迟角为1.35°。

重新设置U1与Sine相位均为0,Delay模块中“Time delay”设定为“75e-6”。13次以上典型谐波FFT分析见表2。

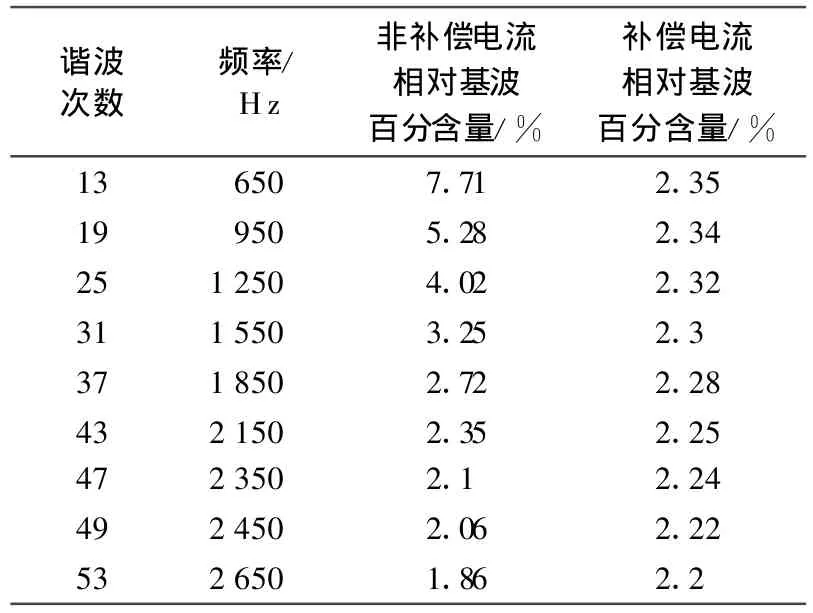
表2 FFT分析结果(75μ s延时)Tab.2 FFT analy sis result(75μ s time delay)

由仿真实验结果可知,最高谐波补偿次数可以达到47次,电流总谐波畸变率补偿前后分别为30.16%,9.97%,补偿效果相对理想。

由仿真实验可得:延时越小,可以补偿的谐波次数越高。

如果要求更高的场合,可以进行互感器相位补偿[5],改用更高速的DSP数字处理芯片等方法。以上虽然是针对信号处理延时做的理论分析和简易模型仿真,但是实际工程应用可以此估算,作为确定补偿次数的依据,有极大的参考价值。

4 补偿次数的设定

首先尽可能采取一切手段减小系统延时。在无法减小信号处理延时的情况下,为了得到更好的补偿效果,必须对补偿次数进行限制,使高次谐波不注入电网。

在DSP处理器的A/D采样之前加一前置低通滤波,将高频分量衰减。电流采样信号经过低通滤波器滤除高次谐波后,再参与谐波电流的检测运算。一阶RC低通滤波器会产生延时,通过仿真分析,前置低通滤波虽然可以有效地抑制高次谐波放大,但是网侧电流总谐波畸变率T HD迅速上升,使得这种抑制谐波放大的方法没有实际意义[6]。

高次谐波采样输入端限制无法实现,可以采用输出端LC或者LRC[7]低通滤波电路进行高频电流输出限制。本文采用3阶LC作为输出逆变器的滤波器[8],如图4所示。

图4 LC低通滤波结构Fig.4 Structure of LC LPF

通过延时估算,图2的简易仿真模型分析,得到补偿最高次数,确定逆变输出的截止频率。在图4输出滤波作用下,使输出电流只补偿截止频率以下的谐波电流,对APF注入电网截止频率次数以上的谐波电流通过LPF滤除[8- 9]。

巴特沃斯3阶低通滤波归一化传递函数[10]:

将截止频率带入进行反归一化得到巴特沃斯系统函数:

系统等效电路如图5所示。

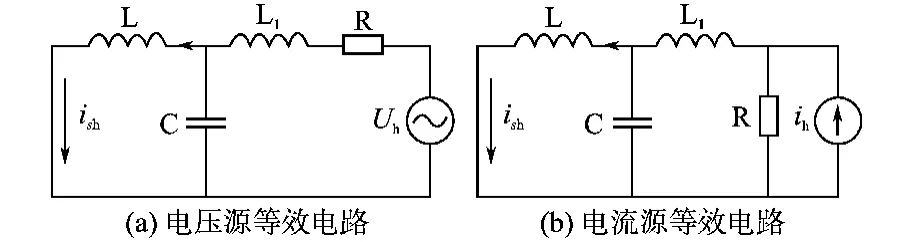
图5 LC低通滤波等效电路Fig.5 Equivalent circuit of LC LPF

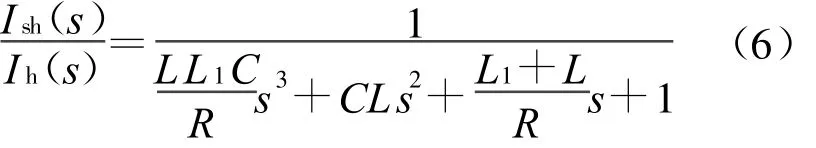
由式(5)和式(6)可得:

逆变器等效内阻和线路阻抗之和假设为3 Ω,这样可以计算得到:

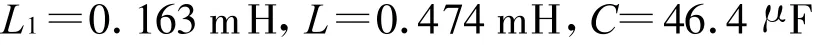
构建APF系统仿真模型见图6。

图6 APF系统仿真模型Fig.6 Simulation model of APF

加入低通滤波前后网侧电流波形及其频谱分析见图7、图8。

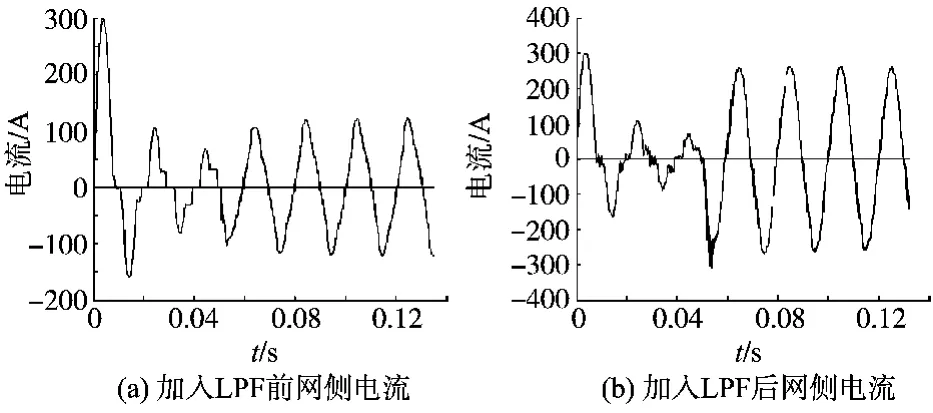
图7 加入 LPF低通滤波前后波形图Fig.7 Wavefo rms before and after adding LPF

从频谱分析可以看出,加入LPF后网侧电流畸变率从16.45%降低到5.71%,从频谱图上看,虽然低次谐波(1 000 Hz以下)没有大幅度减小,但是高次谐波(1 000 Hz以上)基本不存在,取得了较好的效果。

在实际APF装置中,连接电感、滤波电容等相关参数,需要结合现场实际情况和其他因素给予适当调整和优化,使APF达到最佳工作状态。

图8 加入 LPF低通滤波前后频谱图Fig.8 Spectrum before and after adding LPF

5 结论

APF延时对其补偿效果造成巨大影响,尤其是高次谐波放大。本文通过对APF进行延时分析,构建建议模型,初步确定APF系统可以补偿的最高谐波次数。通过在APF与电网连接处并联电容,构成LC低通滤波器,使APF系统只输出补偿低次谐波,实现补偿谐波补偿次数设定,通过仿真验证,取得了较好的效果。

在实际装置中,需要根据不同的负载类型,结合APF补偿效果,反复试验,调整低通滤波参数,同时需要避免滤波电容引起的系统震荡。

[1] 王兆安,杨君,刘进军.谐波抑制与无功功率补偿[M].北京:机械工业出版社,2006.

[2] 肖红霞,范瑞祥.有源电力滤波器延时分析[J].电气传动,2006,36(10):33-36.

[3] GB 1208-1997.电流互感器国家标准[S].

[4] 钟洪浩.新型混合有源电力滤波器研究[D].杭州:浙江大学,2005.

[5] 阳靖,周有庆,刘琨.电子式互感器相位补偿方法的研究[J].电力自动化设备,2007,27(3):45-48.

[6] 鞠建勇.并联有源滤波器工程应用关键技术的研究[D].杭州:浙江大学,2009.

[7] 武健,何娜,徐殿国.三相并联有源滤波器输出滤波器设计方法研究[J].电力电子技术,2004,38(6):16-19.

[8] 陈允平,丁凯,丁建军.并联型有源电力滤波器与电网连接低通滤波器的设计[J].电力系统自动化,2005,29(3):65-68

[9] 史伟伟,蒋全,胡敏强.串联型电力有源滤波器中低通滤波器的设计参数及优化[J].中国电机工程学报,2001,21(11):74-78.

[10][日]远坂俊昭.测量电子电路设计——滤波器篇[M].北京:科学出版社,2006.