GPS软件接收机精确载波频率捕获算法分析与实现*

刘 宁,刘雪瑞

(61365部队,天津300142)

0 引 言

随着软件无线电技术的发展,基于软件结构的GPS接收机正越来越受到人们的重视。与硬件接收机相比,软件接收机成本低,灵活性好,开发周期短,具有高度的可配置性。要利用GPS卫星信号进行导航定位,接收机首先要捕获GPS卫星信号。本文讨论了GPS软件接收机数字中频信号的快速捕获原理,分析了初始捕获后精确载波频率的获取方法,并对该方法进行了改进,提高了软件接收机捕获模块中载波频率的精度。

1 基于FFT的并行码相位搜索捕获原理

GPS信号的捕获是一个二维的搜索过程,需要复现本地C/A码和载波,然后和输入信号作相关获取最大值[1-2]。基于快速傅里叶变换(FFT)的并行码相位搜索捕获方法是对码相位进行并行搜索。首先通过傅立叶变换使处理过程由时域变为频域,使时域中的相关运算变换到频域中的乘法运算,然后再通过逆傅立叶变换得到时域的相关运算结果。此方法称之为循环相关法,其数学模型如式(1)所示:

式中:y[m]表示接收的信号数据;CA[m]表示本地复现的信号;DFT和IDFT分别表示快速傅里叶变换及逆变换;*表示取复数的共轭;R[m]表示相应的接收信号与本地复现信号间的相关值。找出所有R[m]幅值中的最大值,如果这个最大值大于预先设定的门限值,那么信号就捕获成功。

2 精确载波频率获取算法

由1 ms数据捕获得到的频率分辨率大约是1 kHz,这对于跟踪环来说过于粗糙,需要的频率分辨率应当在几十赫兹以内[3]。采用长的数据进行捕获,可以提高频率分辨率,但长数据的FFT运算量大,非常耗时,而且长数据段内C/A码发生相移的可能性相对要高。

通过相位关系可以得到精确载波频率[4]。为了将C/A码从输入信号中剥离掉,根据捕获得到的C/A码初始相位和载波频率(1 kHz分辨率)生成本地复现信号,并与输入信号相乘(即作DFT运算),输出信号可以表示为

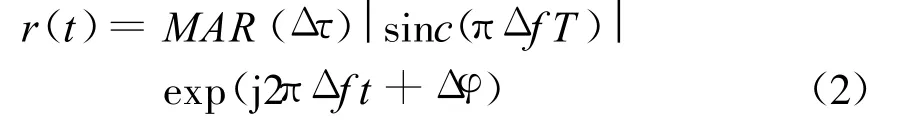
式中:M为累加的采样值点数;A为信号的幅度;R(◦)为PRN码的自相关函数;Δ τ为输入信号与本地复现信号C/A码相位偏差;T为积分累加时间;Δ f为输入信号与本地复现信号的频差;Δ φ为初始相位差。此时,C/A码已从输入信号中剥离掉,输出信号r(t)为cw信号,通过相位关系就可以求得精确频差 Δ f.

如果m时刻的输入信号与本地复现信号相乘,输出信号r(t)在m时刻的初始相位可由式(3)得到

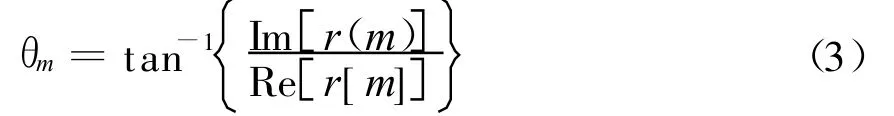
式中,Im和Re分别表示复数的虚部和实部。因为在短时间内输入信号的频率变化不大,忽略短时间内的频率变化,相同的初始捕获频率,对应的频差Δ f可以看作是定值。在m时刻之后间隔不长的n时刻,输出信号r(t)在n时刻的初始相位为

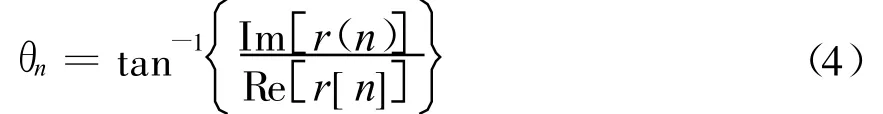
利用这两个相位角可得到精确的频差[5]

由此式得到的频率分辨率比DFT得到的要精确得多。为了保证得到的频差不模糊,相位差θnθm必须小于2π,即相位差不能存在整周模糊度。如果用间隔1 ms的两段数据求取精确频差,捕获得到的载波频率与输入信号的频率之差就应小于1 kHz。

但是,实际问题要复杂一些。因为在两组相邻数据中,导航数据可能会引起180°的相移,这时就不能把输出信号看作cw信号。这就会将1 ms时延数据的模糊带宽限制在 250 Hz。如果频偏±250 Hz,1 ms时延对应的相位差是±π/2。如果频偏+250 Hz,对应的相位差是+π/2,然而,由导航数据产生的π相移将把相位角变为-π/2(+π/2-π),这对应于频偏-250 Hz的情形。如果在确定精确频率时不考虑相位跳变的话,结果会有500 Hz的频偏。为了避免这种情况,最大频差必须小于250Hz.如果最大频差限制在±200 Hz,相应的相位差就是±2π/5,若存在 180°相移,相差就是3π/5,大于2π/5。因此,相差可用来在不产生误差频移的情况下,确定精确频率[1]。

3 算法改进

从以上分析可以看出,要获得精确载波频率,首先要将载波频率的分辨率从1 kHz提高到400 Hz,即使频率精度保持在200 Hz以内。文献[1]中的方法是对同1 ms数据进行两个DFT操作(信号相乘),一个比初始捕获频率值低400 Hz,另一个高400 Hz.然后将三个输出幅值中最大值所对应的频率作为新的载波频率。由于噪声的影响,三个幅值中的最大值很可能并不对应频差最小的频率,此时的频率偏差将大于400 Hz,得到的相位差大于2π/5,并且越修正越大。为了使频率精度精确地保持在200 Hz以内,本文采用对同一连续5 ms的数据进行相干积分,然后取累加后的三个幅值中的最大值所对应的频率作为新的载波频率。由于采用了相干积分,消弱了噪声的影响,使得载波频率能够精确地保持在200 Hz以内。

4 捕获实例及结果分析

4.1 模拟数据仿真算例

实验首先用模拟的两组GPS信号来实现基于FFT的并行码相位搜索捕获,并用上述算法进行频率精化。仿真产生GPS中频数据的主要参数为:卫星号为21,采样率5 MHz,中频1.25 MHz,多普勒频移-1455 Hz,C/A码初始相位为2151。为了分析算法性能,模拟产生两组GPS信号,一组为加高斯白噪声的弱信号;一组为不加噪声的强信号。捕获采用的数据长度为1 ms,图1为捕获结果。

图1(a)为弱信号得到的捕获结果,噪声很大,效果不明显;图1(b)为强信号得到的捕获结果,噪声很小,峰值高出图1(a)很多,效果明显。

模拟信号采样率为5 MHz,1 ms对应5000个数据点。考虑到接收机的实时性,为了减少捕获过程中的运算量和实现的复杂度,采用的捕获方案不直接对5 MHz的数据点做FFT,而是先以2.048 MHz对数据进行二次采样,变成一个点数较少的,为2的n次幂的点序列,以便于进行基2的FFT运算。此时,1 ms对应2048个数据点。二次采样后,C/A码仍然具有良好的自相关性,保证了捕获的顺利进行[2],但捕获灵敏度会有所降低。在图1中,捕获的C/A码初始码相位为881,对应于 5 MHz的原始数据为2151(881×5/2.048)。表1列出了捕获过程得到的初始载波频率和频率精化后的载波频率:

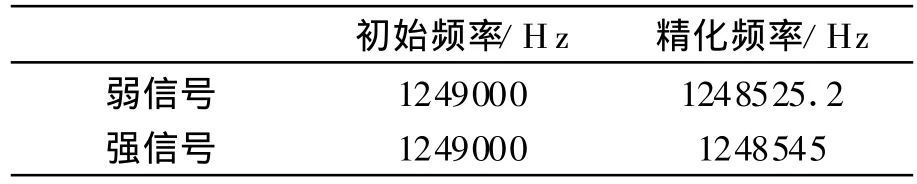
表1 模拟信号捕获及频率精化结果

从表1中可以看出,捕获得到的初始载波频率与精确载波频率(1248545 Hz)差-455 Hz.对于弱信号,经频率精化后的载波频率与精确频率差19.8 Hz;对于强信号,频差为0 Hz,得到了精确的载波频率。由此可见,根据相位关系的频率精化方法可以将捕获的载波频率精度提高到几十个赫兹以内,符合一般信号的跟踪需求。

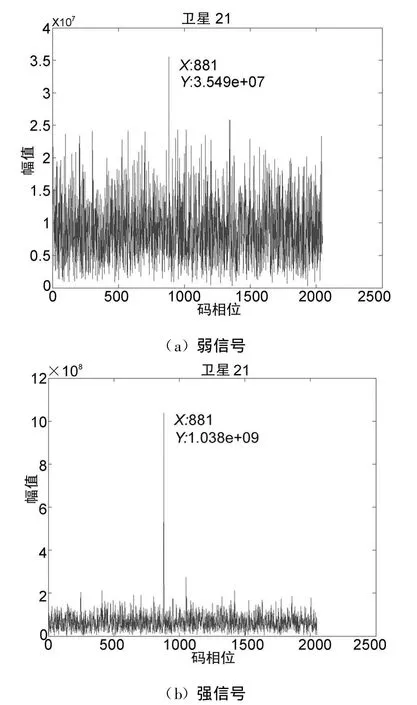
图1 模拟GPS信号捕获结果对比

4.2 实测数据捕获实验以及结果分析

本实验处理的数据来自于由前端硬件采集的实测数据,采样频率为38.192 MHz,中频(IF)为9.548 MHz,总共有8颗可见卫星。下面以其中的两颗卫星来进行捕获实验,分别为18号星和21号星。捕获采用的数据长度为1 ms.同样,捕获过程中对中频信号进行了二次采样,由每毫秒38192个数据点重采样成2048个数据点进行捕获。图2为两颗星的捕获结果:

从图2的对比中可以看出,21号星受到噪声的影响比18号星大一些,信噪比要比18号星低。表2列出了初始捕获后得到的C/A码初始码相位和初始载波频率以及进行频率精化后得到的载波频率:

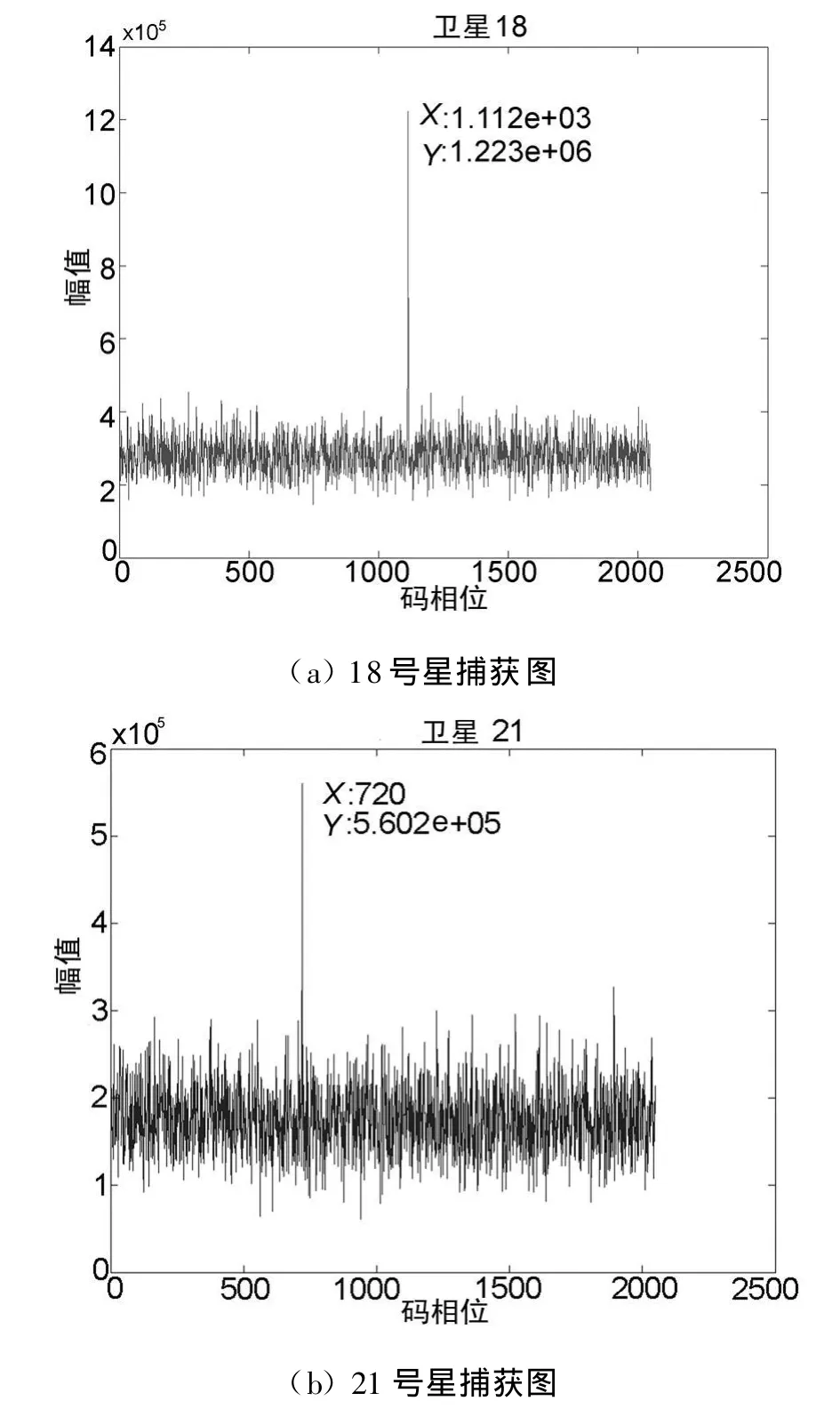
图2 实测数据捕获结果对比

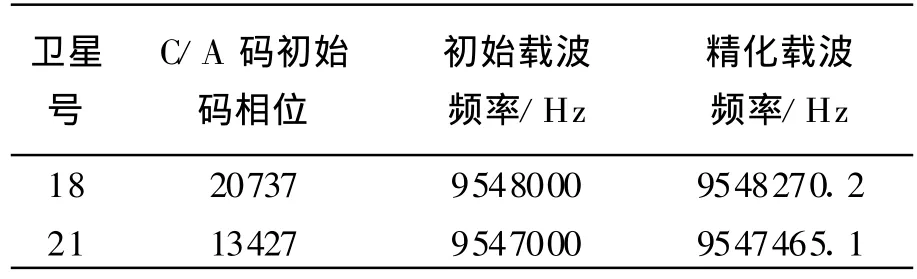
表2 实测数据捕获及频率精化结果

从表2中可以很直观地看到精确的载波频率和初始的载波频率相差多达几百赫兹,可见初始捕获得到的载波频率是不满足后续跟踪模块要求的。

为了检测经频率精化后得到的载波频率是否符合信号跟踪模块的需求,本文以精化后的载波频率作为跟踪模块的输入,分别对18号星和21号星进行了跟踪实验,图3为起始600 ms的跟踪输出结果:

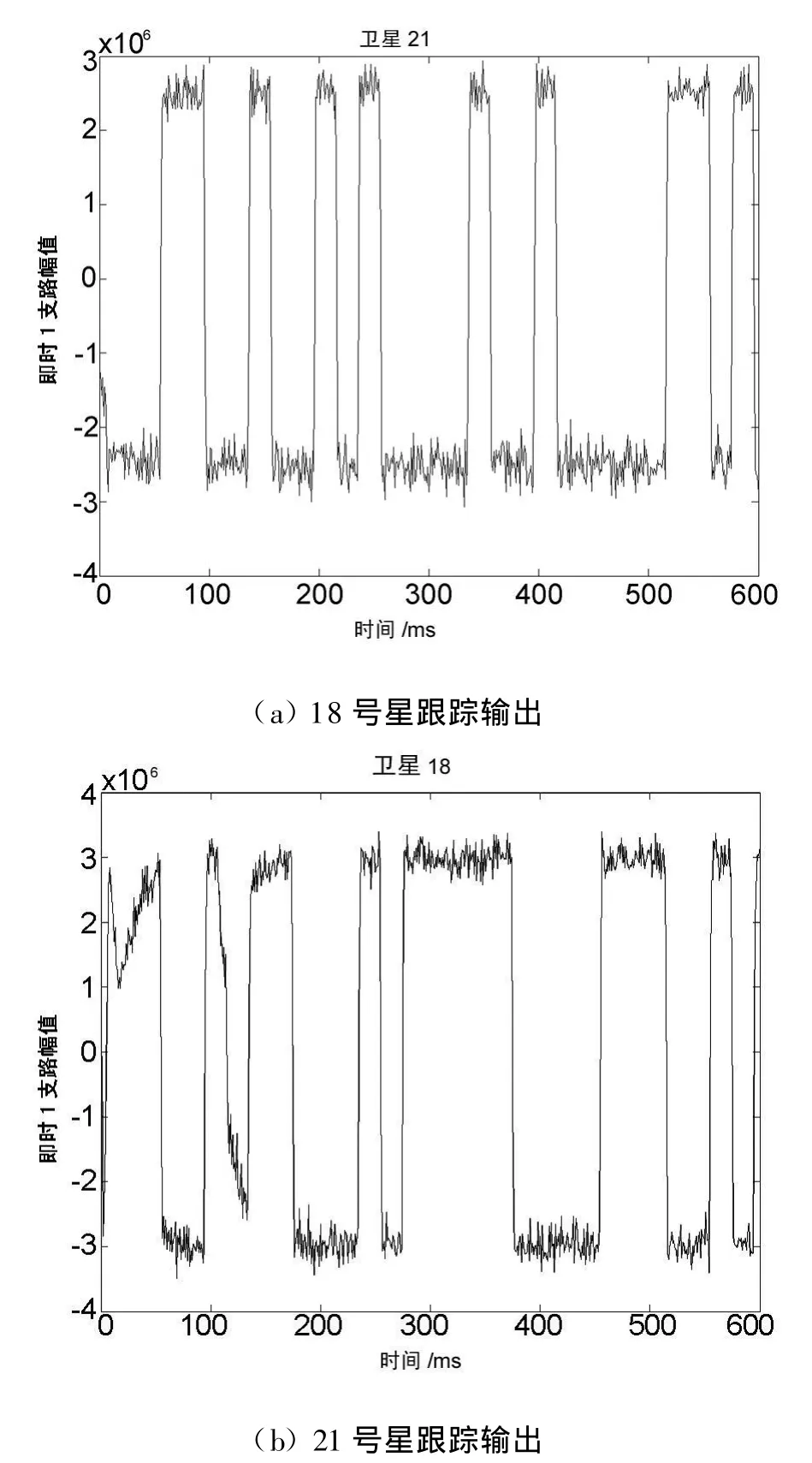
图3 实测数据跟踪输出对比

从图3中可以看出,跟踪模块以频率精化后得到的频率作为输入,成功地跟踪上了18号星和21号星的信号,说明经频率精化后得到的精确频率满足跟踪模块的需求,以上述方法对初始捕获后得到的载波频率进行精化的方法是可行的。图3中18号星和21号星跟踪输出的差异在于18号星从一开始就平稳地跟踪上了,而21号星虽然开始也跟踪上了,但跟踪输出有些波动,随后才趋于平稳。这是因为21号星信号噪声比18号星要大些,在噪声的影响下,频率精化得到的载波频率精度没有18号星的载波频率精度高。

5 结 论

基于FFT的并行码相位搜索捕获算法可以快速地捕获到GPS信号。在获得C/A码初始相位和载波频率后,通过相位关系可以得到精细频偏,从而获得更精确的载波频率,可以满足GPS跟踪模块对一般信号的跟踪需求。

[1] James Bao-Yen T.Fundamentals of global positioning system receivers:A software approach[M].2 ed.John Wiley&Sons.Inc,2005.

[2] 唐 斌.卫星导航软件接收机关键技术研究[D].北京:装备指挥技术学院,2007.

[3] 李作虎.GPS软件接收机技术仿真实验研究[D].郑州:信息工程大学,2008.

[4] 徐卫明,刘雁春,朱穆华.GPS中频信号快速捕获技术分析[J].测绘科学,2007,32(5):98-100.

[5] 高洁雯,柳林涛,杨 光.基于软件实现GPS信号捕获以及获取精确载波频率[J].测绘科学,2007,32(5):14-16.