精密单点定位估计GPS卫星的P1-C1码偏差及稳定性分析*

唐 龙,张小红,吕翠仙,高 攀

(武汉大学测绘学院,湖北 武汉430079)

0 引 言

利用GPS进行测量时,在一些情况下(如使用单频接收机C1/X型和C1/P2型接收机),必须考虑仪器偏差(有的文献也称为硬件延迟)的影响[1-2]。不同类型的测距码以及不同频率的载波所引起的仪器偏差不同,C1、P1、P2对应的仪器偏差分别为:BC1、BP1、BP2[2]。绝对偏差往往无法得到,通常所求的是它们之间的相对值—P1-C1和P1-P2码偏差(diffe-rential code bias,DCB)。文献[3]在选择一个参考卫星的条件下,通过星间差分求出每颗卫星与参考卫星的相对DCB,进而求出每颗卫星的DCB。欧洲定轨中心(Center for Orbit Determination in Europe,CODE)自1057 GPS周便开始计算卫星和接收机的仪器偏差,计算方法与文献[3]类似,只是参考基准不同,其基准为所有卫星的DCB之和为零[4]。

目前,精密单点单位(precise point positioning,PPP)技术已比较成熟,可实现静态mm到cm的定位精度[5]。而且由于采用非差观测值,考虑了各种误差的影响,使得PPP不仅可以用来定位,还可以进行各种数据分析。基于这种思想,文献[4,6]提出了利用PPP估计DCB的方法。笔者在T riP软件平台的基础上研制了估计P1-C1码偏差的处理模块,通过大量的数据处理分析,给出了利用PPP技术估计P1-C1码偏差的精度及指标。

1 PPP估计P1-C1码偏差的数学模型

利用IGS发布的卫星和钟差产品,并考虑其它可精密模型化的误差改正后,基于P1、P2观测值的精密单点定位无电离层组合观测方程可简化为

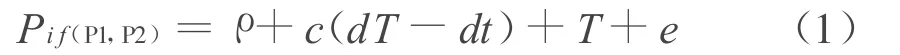
式中:Pif(P1,P2)是无电离层组合伪距观测值;ρ为卫星与接收机之间的几何距离;c为光速;dT为接收机钟差;dt为卫星钟差;T为对流层延迟;e为观测噪声及其它残差。

1)式中没有考虑卫星码偏差,其原因是IGS在估计卫星钟差时也采用相同的观测方程[1,4,6],此时偏差可以认为包含在卫星钟差里面。如果利用C1码观测值来代替P1码观测值,组成无电离层组合观测方程,就需要考虑P1-C1码偏差,此时的观测方程为

式中:Pif(C1,P2)为C1、P2无电离层组合伪距观测值;为卫星的P1-C1码偏差。

需要说明的是,式(1)和式(2)都没有考虑接收机的码偏差。这是因为,在非差定位时,接收机的码偏差被接收机钟差吸收了。

采用传统的PPP模型,可以精确求得ρ、dT以及T,dt可以利用精密钟差文件内插得到。那么就可以得到估计BP1-C1的观测方程:

由(3)式可知,只需一个观测方程便可以确定每颗GPS卫星的P1-C1码偏差。对多个观测值可采用最小二乘原理进行平差求解:

式中:^BP1-C1是平差值;B为设计矩阵;L为观测值矢量;P为权矩阵。

2 数据处理与分析

CODE每个月发布一次卫星的DCB数据,为了使结果具有可比性,本文对 BRUS、GODE、SHAO和NIST四个IGS跟踪站2010年10月份全月的观测数据(年积日274～304)利用上述方法估计P1-C1的码偏差。四个站分布在欧洲、亚洲和美洲,位于中低纬地区。

2.1 P1-C1码偏差随时间的变化规律

分别利用四个站的观测数据计算所有观测弧段超过4个小时的观测卫星的P1-C1码偏差,结果如图1所示。

图1 四个站所算卫星P1-C1码偏差

从图1可以看出,每颗卫星的P1-C1码偏差在一个月内变化比较平缓,GODE站计算的码偏差变化幅度略大,这可能与观测数据质量有关。由此说明,以每个月的平均值作为仪器偏差改正数是合理的,这也和CODE每个月发布一次卫星的DCB数据是一致的。

我们分别计算了四个站求得的卫星P1-C1码偏差一个月的平均值,结果如图2所示。

从计算结果看,卫星的P1-C1码偏差达到分米级。因此,在精密定位中,必须加以考虑。

2.2 不同测站计算P1-C1码偏差的差异

为了比较不同测站所算卫星P1-C1码偏差的差异程度,选取这四个站均能观测到,且观测时间大致相同的卫星进行比较,结果如表1所示(以SHAO站为参考站)。

图2 四个站所算卫星P1-C1码偏差一个月的平均值

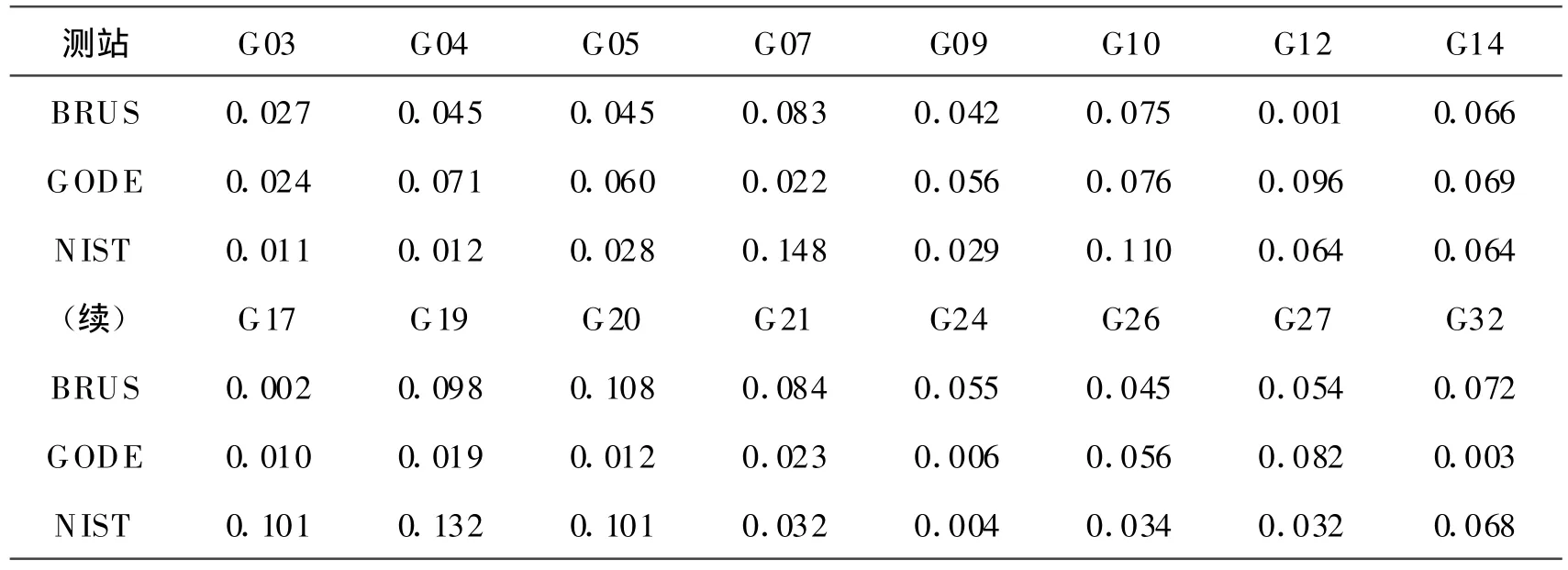
表1 不同测站计算卫星P1-C1码偏差值比较

从表1可以看出,四个站所算卫星的P1-C1码偏差值比较接近,大部分数据偏差在0.1 m之内。这说明卫星的P1-C1码偏差值依赖于卫星,与接收机无关。事实上,卫星的P1-C1码偏差是由于编码在卫星L1载波上的信号不一致产生的。当然由于不同接收机观测数据质量不尽相同,对解算结果会有一定的影响。

2.3 与CODE发布DCB结果的比较

为了评价利用PPP技术解算得到的卫星P1-C1码偏差值的精度,可以将其与CODE提供的卫星P1-C1码偏差进行求差比较。图3显示了二者比较结果。

从图3可以看出,二者差值主要分布在5个cm左右,大部分差值均位于1 dm以内。这表明利用PPP技术解算的结果与CODE提供的值吻合的比较好。若将CODE提供的卫星P1-C1码偏差值作为参考真值,计算每个站估算的P1-C1码偏差的RMS值,结果见表2.若我们进一步取四个站相同卫星的平均值作为相应卫星的估算值,以CODE提供的卫星 P1-C1码偏差值作为参考真值,RMS可降至0.039 m.

图3 基于PPP解算的P1-C1码偏差值与C ODE结果的比较

表2 不同测站估算结果的RMS值

这表明:单站解算P1-C1码偏差的精度可优于1 dm,利用多个站求解P1-C1码偏差的精度要比单个站解算的精度高。如果利用全球的IGS站观测数据来计算卫星端的P1-C1码偏差,其精度有望达到cm级,结果也将更可靠。

3 结 论

通过对BRUS、GODE、SHAO以及NIST四个跟踪站2010年10月份的观测数据进行处理,采用基于PPP的方法估计了卫星的P1-C1码偏差,并对处理结果进行了深入分析,得出了如下结论:

1)每颗卫星的P1-C1码偏差在一个月内变化比较平缓。

2)不同站求得的卫星P1-C1码偏差差距不大,说明卫星P1-C1码偏差只与卫星有关,与接收机无关。

3)采用基于PPP的方法估计的卫星P1-C1码偏差,单个站算得的精度优于1 dm。可以采用多个站联合求解的方法,来提高解算精度和可靠性。

因此,采用PPP估计卫星的P1-C1码偏差的方法是可行的。

[1] Le A Q,Christian T.Single-frequency precise point positioning with optimal filtering[J].GPS Solutions,2007(11):61-69.

[2] 张小红,李星星,郭 斐,等.GPS单频精密单点定位软件实现与精度分析[J].武汉大学学报◦信息科学版,2008,33(8):783-787.

[3] Gao Y,Lahaye F,Heroux P.Modeling and estimation of C1-P1 bias in GPS receivers[J].Journal of Geodesy,2001(74):621-626.

[4] Leandro R F.Precise point positioning with GPS:A new approach for positioning,atmospheric studies,and signal analysis[D].New Brunswick:University of New Brunswick,2009.

[5] Kouba J,Heroux P.Precise point positioning using IGS orbit and clock products[J].GPS Solutions,2001,5(2):12-28.

[6] Leandro R F,Langley R B.Estimation of P2-C2 biases by means of precise point positioning[C]∥Proceedings of ION,2007:225-231.