数控机床大推力永磁同步直线电机控制方法
王 潇
(北京信息科技大学机电工程学院,北京 100192)
传统的传动机构如齿轮、蜗轮、皮带、丝杠、滚珠丝杠、联轴器、离合器等中间传动机构,容易产生很多如:较大的转动惯量、弹性形变、反向间隙、摩擦、振动、磨损等问题,所以不仅减小了传动效率,而且还增加了成本,降低了系统的可靠性。虽然这些传动机构性能已经得到了改善,但是其间接传动的本质不能从根本上解决。于是“直接驱动”概念应运而生,直接驱动是指不使用任何中间传动机构,直接将动力源与负载相连进行驱动。这种传动具有结构简单、动态响应快、速度和加速度大、精度高、振动和噪声小等优点。
直线电机就是直接驱动的装置,其中控制技术是直线电动机设计和应用的重点。PID调节是最早出现的一种自动控制方法,控制简单而且效果显著。尤其是在高精度运动控制中,运用多闭环控制已经越来越广泛,伺服系统一般是三环系统,外环为位置环,内环依次为速度环、电流环。电机三环控制框图如图1所示。但是传统的PID控制算法不能对摩擦力、负载扰动等外界干扰及时消除,直线电机对负载扰动、摩擦力敏感,极易产生较大的稳态误差,降低了控制精度。基于以上问题,提出抗干扰较强的PID+前馈算法,并用实验验证这种控制方法可以提高控制精度[1-2]。
1 直线电机运动控制原理
直线电机进给机构采用闭环控制,使用Renishaw高精度直线光栅尺作为位置反馈元件,安装于电机平台底部,与平台固定为一体,由于没有与电机直接接触,不会对直线电机运动产生磨擦力。光栅反馈信号首先进入放大器编码器输入端口,并由放大器的等量输出端口反馈到PMAC卡,组成双闭环反馈,根据光栅尺反馈的脉冲信号即可计算直线电机当前位置,由控制器的PID调节器根据目标位移与实际位移的差值自动调节电机的控制参数,完成所需的进给。闭环控制原理,如图5所示[3]。

图1 三环伺服系统控制框图

图2 闭环控制原理图
PMAC控制的直线电机伺服系统是一个高速动态系统,复杂的控制算法无法在如此短的时间内完成伺服计算,所应该采用计算量比较小的伺服算法。传统的PID环节是偏差控制器,被控制量需要偏离设定值才能通过偏差进行控制,存在一定的滞后性;由于系统受到扰动,再加上系统本身结构和参数的变化而产生的误差,不能在闭环系统中消除,所以需要对系统进行补偿,抵消扰动对系统的影响,即所谓的扰动补偿。控制框图如图6所示[4]。

图3 带前馈补偿PID闭环控制
图3为带前馈的控制结构框图,其中,R(s)为系统输入;E(s)为系统误差;C(s)为系统的输出;G(s)为PID控制器传递函数;Gp(s)为被控对象的传递函数;F(s)为前馈环节的传递函数。得出带前馈的系统误差传递函数

式(1)说明,当前馈函数满足F(s)=Gp(s)-1时,误差函数为0,则C(s)=R(s)。说明无论输入信号如何变化,系统的误差始终为0。前馈补偿比只按误差控制的闭环系统效果好。通常前馈微分阶次为2时即可获得满意的控制效果。
PMAC在传统PID控制算法的基础上增加了速度和加速度的前馈控制,其中,速度前馈用于减小由于微分增益的引入所引起的跟随误差,加速度前馈用于减小系统惯性所带来的跟随误差。PMAC嵌入的PID和前馈控制的控制算法如图4所示[5]。

图4 PMAC算法控制框图
图4中,Kp比例增益,为系统提供刚度;Kd微分增益,提供系统稳定需要的阻尼;Kvff速度前馈增益,减小因阻尼引起的跟随误差;Ki积分增益消除稳态误差;Kaff加速度前馈增益减小系统惯性带来的跟随误差。
其控制算法的实际公式如下

其中,DACout(n)为16位的伺服周期输出命令转换成-10~+10 V;Ix08为电机x的一个内部位置放大系数;Ix09为电机 x速度环的一个内部放大系数;FE(n)是伺服周期n内所得的跟随误差,即为该周期内命令位置和实际位置的差值;AV(n)是伺服周期n内的实际速度,即为每个伺服周期最后两个实际位置的差值;CV(n)是伺服周期n内的指令速度,即为每个伺服周期最后两个指令位置的差值;CA(n)是伺服周期n内的指令加速度,即为每个伺服周期最后两个指令速度的差值;IE(n)是伺服周期n的跟随误差的积分,大小为
2 实验用直线电机简介
该电机应用于龙门五轴加工中心立柱上,最大推力12000 N,低速可至1 m·min-1,最高速度可达1 m/s。具有大推力、速度范围宽特点,是提供直线进给的优良系统,电机实物如图4所示。

图5 永磁同步直线电机实物图
直线电机底部为次级板,其结构呈U型,次级长1.32 m,宽0.26 m,高0.17 m,材料由ZG35铸造而成,表面镀锌,N级磁钢和S级磁钢交替贴在次级表面时,并且要使同一极板两侧极性相反,同一侧的两片相邻磁钢用分隔条隔开,用胶粘牢固后,灌环氧树脂密封成整体。

图6 永磁同步直线电机结构简图
直线电机的初级是由两块安装板并联在一起,长1.4 m,宽0.36 m,高0.22 m,由铸铁35铸造而成,经过加工后,表面镀白锌,水冷板介于次级线圈与安装板之间,由铸铝制成,内嵌有铝管,用于通水为初级线圈冷却。
3 直线电机的测试实验
PMAC执行程序Pewin提供了调节PID参数的工具PMAC Tuning Pro,可以方便地调节PID参数。打开Pewin首先调节系统的开环特性,开环特性调节完毕后,调整系统的稳态特性,分别调节PID参数中的比例增益、微分增益、积分增益,使系统阶跃响应曲线稳态误差为0,并且超调量不要过大,得到良好的误差曲线。最后调节系统的动态特性,以正弦信号为输入调节系统的跟随误差,根据正弦响应曲线调整适当的速度、加速度前馈系数,使系统的跟随误差最小,得到较好的动态响应曲线。
经反复调试比较,得到图7的阶跃线响应曲线。从图中可以看出,系统有较好的阶跃响应曲线,证明PMAC卡对直线电机的控制具有良好的效果。

图7 阶跃响应曲线
图8为稳态时给定速度为10 m·min-1时,给定速度与实际速度的比较曲线。
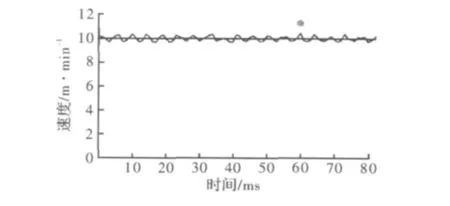
图8 速度对比曲线
速度波动

速度波动在误差允许范围之内。
图9为系统的动态响应曲线,从曲线上可以看出,最大的跟随误差为420 μm。

图9 动态响应曲线
4 结束语
依据直线电机的伺服特点,提出了前馈+PID算法的控制策略,运用该控制策略使直线电机具有良好的速度稳定性以及较小的跟随误差。伺服算法嵌入到Turbo Pmac Clipper中,利用PMAC Tuning Pro2可以方便地对系统的控制参数进行调节,为以后直线电机朝着高速度、高精度的方向发展提供了支持。
[1] Delta Tau.Turbo PMAC usual manual[M].USA:Delta Tau Data System,Inc,2008.
[2] 叶云岳.直线电机的原理与应用[M].北京:机械工业出版社,2000.
[3] 黄笑天,张建明,庞长涛,等.微铣削系统中直线电机的应用研究[J].航空精密制造技术,2007,43(2):21-23.
[4] YUSUF A.数控技术与制造自动化[M].罗科学,译.北京:北京化学工业出版社,2002.
[5] 郭庆鼎,孙宜标,王丽梅.现代永磁电机交流伺服系统[M].北京:中国电力出版社,2006.

