利用平面GPS高程拟合法求均值的讨论
张想平
(兰州市城市建设设计院,甘肃兰州 730030)
利用平面GPS高程拟合法求均值的讨论
张想平∗
(兰州市城市建设设计院,甘肃兰州 730030)
主要讨论了利用平面GPS高程拟合法求均值的原理和方法,并引用实例对拟合高程与四等水准高程进行了比较,就比较结果进行了讨论。
高程拟合;平面;求均值
1 前 言
近年来,GPS技术在测绘领域得到了广泛的应用。特别是在控制测量方面,由于其平面测绘成果精度高、观测方法简便、两点之间不需要通视和全天候观测等优点而成为现代测绘技术的主要手段。我们知道,利用GPS定位技术获取的测量成果经过三维约束平差后,我们能够获取得到在当地坐标系下精度较高的点位平面坐标值。但是,GPS观测所得到的是大地高,大地高也称为椭球高,是以参考椭球面为基准面的高程系统。某点的大地高是该点到通过该点的参考椭球的法线与参考椭球面的交点间的距离,是一个纯几何量,不具有物理意义。同一个点,在不同的基准下,具有不同的大地高。而在实际的应用中,我们采用的是正常高。正常高是以似大地水准面为基准的高程系统。某点的正常高是该点到通过该点的铅垂线与似大地水准面的交点之间的距离。大地高与正常高之间有如下几何关系:H=Hγ+ζ。ζ为高程异常。为了确定出正常高,需要求出高程异常数据。求解高程异常数据的方法通常有等值线图法、地球模型法、高程拟合法等多种方法。高程拟合法是比较常用的GPS高程求解方法。
2 高程拟合法基本原理
所谓高程拟合法就是利用在范围不大的区域中,高程异常具有一定的几何相关性这一原理,采用数学方法,求解正常高或高程异常。利用高程拟合法求解高程异常通常有以下三种方法。
(1)常数法,也叫零次多项式法:ζ=a0
(2)平面拟合法,也叫一次多项式法:

(3)曲面拟合法,也叫二次多项式法:

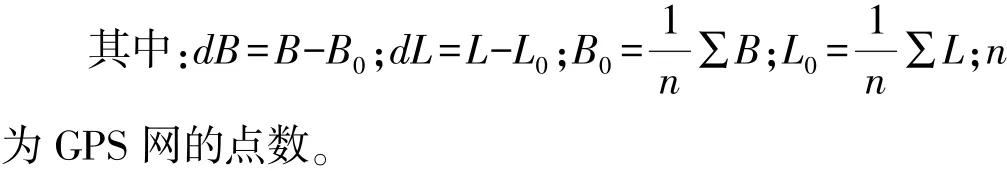
利用公共点上GPS测定的大地高和水准测量测定的正常高计算出该点上的高程异常ζ,存在一个这样的公共点,就可以依据上式列出一个方程:
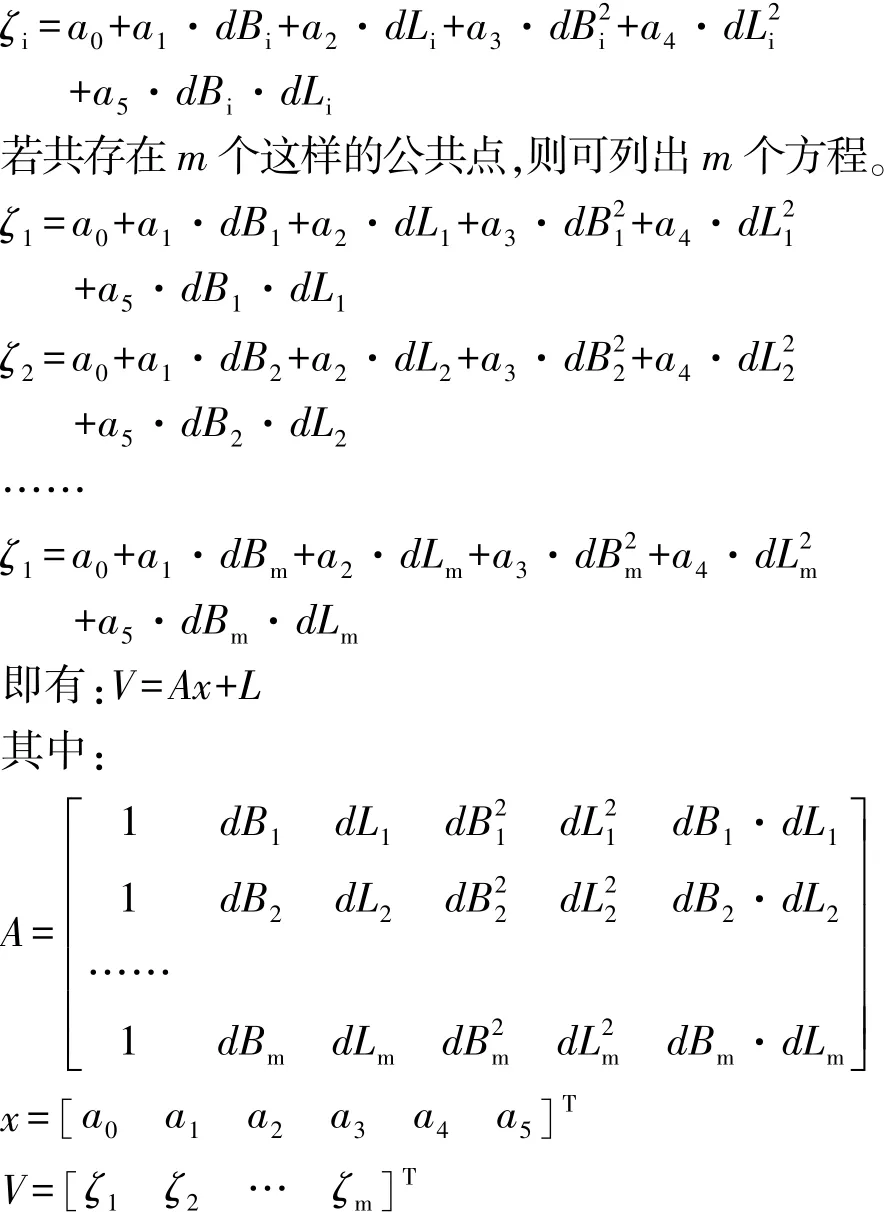
通过最小二乘法可以求解出多项式的系数:

其中:P为权阵,它可以根据水准高程和GPS所测得的大地高的精度来加以确定。
3 选择平面拟合法求均值的原理和优点
(1)选择平面拟合法求均值的原理
选择平面拟合法求均值就是在进行高程拟合的区域内,先选择适当的3个或4个已知高程点确定进行高程拟合的平面,利用已知高程点的大地高和正常高求解出一组已知高程点的高程异常特征值ζ,根据ζ=a0+a1·dB+a2·dL的原理,解算出式中的α0、α1、α2,在将α0、α1、α2代入ζ=a0+a1·dB+a2·dL中,从而解算出高程拟合区域内其他GPS观测点的高程异常值ζ,在利用正常高和大地高的关系式H=Hγ+ζ解算出高程拟合区域内其他GPS观测点的一组正常高。(上述计算原理较为复杂,但在GPS观测数据的解算软件中都有高程拟合的步骤,可以任意的选择高程拟合的方式,因此,利用GPS观测数据的解算软件进行高程拟合的解算十分简单,只需在解算软件中输入已知高程点的高程而已。)利用同样的办法,进行高程拟合的区域内再选择另外的3个或4个已知高程点(可以选择一到两个与前次相同的已知高程点,这样可以减少所需要的已知高程点的数量。)确定进行高程拟合的另一个拟合平面,从而解算出高程拟合区域内另外一组GPS观测点的正常高。诸如此类,我们可以利用高程拟合区域内所有的已知高程点解算出高程拟合区域内好几组GPS观测点的正常高,通过比较同一GPS观测点的几组正常高值,剔除掉同一GPS观测点中较差比较大的一两组正常高,再将剩余几组GPS观测点的正常高取平均值作为最终的高程拟合值。
(2)选择平面拟合法求均值的优点
首先,我们知道,GPS高程拟合的方法是一种纯几何的方法。因此,普通的高程拟合方法(尤其是选择常数法)一般仅适用于高程异常变化较为平缓的地区(如平原地区),其拟合的准确度可达到一分米以内。对于高程异常变化剧烈的地区(如山区),其准确度有限,这主要是因为在这些地区,高程异常的已知点很难将高程异常的特征表示出来。而利用求均值法可以有效消除高程异常变化剧烈而带来的高程异常不确定的问题。
其次,选择合适的高程异常已知点的问题:所谓高程异常的已知点的高程异常值一般是通过水准测量测定正常高、通过GPS测量测定大地高后获得的。在实际工作中,一般采用在水准点上布设GPS点或对GPS点进行水准联测的方法来实现,为了获得好的拟合结果要求采用数量尽量多的已知点,它们应均匀分布,并且最好能够将整个GPS网包围起来。由于常数拟合法的可靠性较低,我们一般不采用该方法。采用平面拟合法要确定3个参数,需要3个以上的已知点,最好每次拟合选用4个已知点,这样我们就可以将两个已知点选择在高程拟合区域内的中间,两个已知点选择在高程拟合区域内的两头即保证了已知点的分布均匀,又能够将整个GPS网包围起来,更重要的是需要已知点高程点数不多,(6个已知点就可以选择5种以上不同的拟合方案。)大大减少了GPS点进行水准联测的工作量。而曲面拟合则不同,该方法要求确定6个参数,则需要6个以上的已知点,要保证已知点均匀分布且能够将整个GPS网包围起来,则已知点必须分布在整个拟合曲面内,这大幅度增加了GPS点进行水准联测的工作量。
4 应用实例
(1)南山路是兰州市政府规划的铁路以南的一条项重要道路,该路是兰州市政府规划的贯穿整个兰州市的四条东西大通道之一,也是铁路以南唯一一条东西走向的道路。该路的建成将对铁路以南地区的经济发展起到极大的带动作用。去年9月,兰州市城市建设设计院受兰州市城投公司的委托,对该工程布置了大型的GPS控制网。该控制网东西向长约35 km,南北向长约0.8 km,最大高差100 m左右。笔者就该控制网利用部分已知水准点应用平面拟合法求均值的方法进行了拟合,拟合时每次选用分布在测区东面的N1、N2、N3三个已知点中的两个点、分布在测区中间的已知点N6、分布在测区西面的已知点N17或N19四点构成拟合平面并用南方GPS平差软件进行数据解算,然后用Excel电子表格格式导出解算结果,最后取5次解算结果的均值作为高程拟合的最终结果,结果如表1所示。
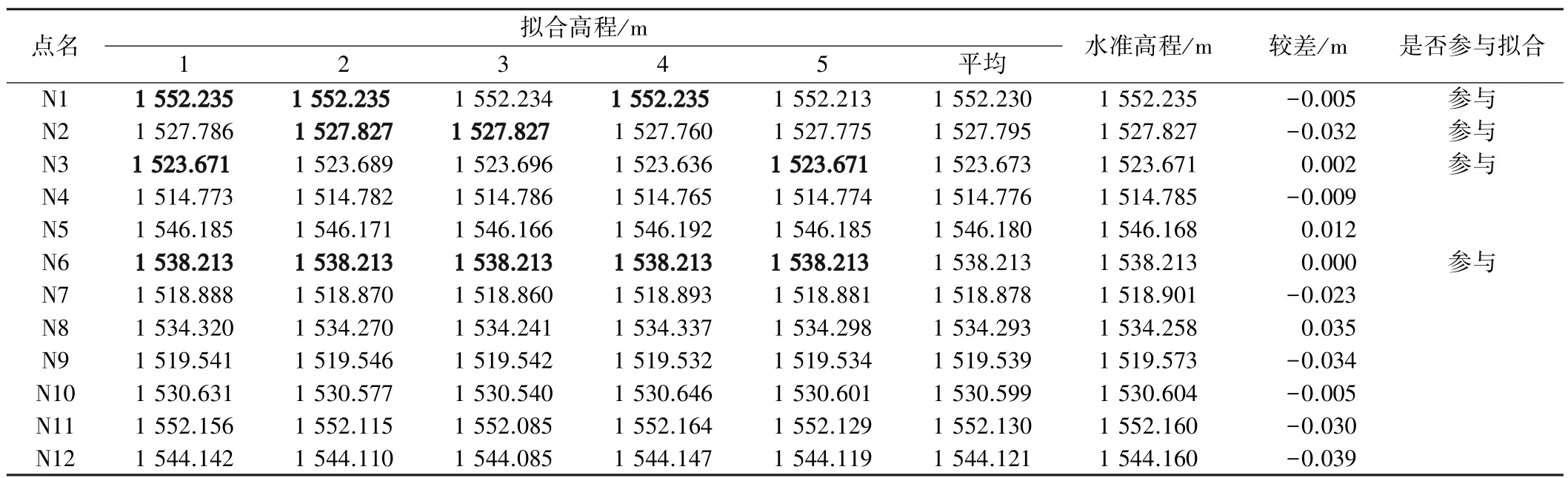
兰州市南山路工程GPS高程拟合成果表 表1

备注:表中每列粗体字为本次拟合参与解算高程点。
(2)彭家坪地区四条道路工程:兰州市彭家坪地区是兰州市政府新批准的高新开发区,是未来兰州市城市规划的第八城市组团,其基础设施建设特别是城市道路的建设,对该地区的经济发展起到极大的带动作用。彭家坪地区四条道路工程正是为了适应这一形势的发展而启动的。去年8月,我们对该工程布置了一个小型的GPS控制网和水准网。笔者就该控制网利用已知水准点应用平面拟合法求均值的方法进行了拟合,并就拟合结果和四等水准结果进行了比较,结果如表2所示。

兰州市彭家坪路网工程GPS高程拟合成果表 表2
5 结 论
通过以上两表的比较可以发现,笔者只选择了5种不同的拟合方案,而且每个工程只有6个或7个已知水准点参与拟合,应用平面拟合法求均值的方法进行高程拟合,绝大部分点的拟合高程与四等水准高程的较差在±30 mm左右,甚至有许多点的较差达到了10 mm以下,只有一个点的拟合高程与四等水准高程的较差在59 mm左右,如果选择的拟合方案更多些,其精度会更高些。我们还发现,就单次拟合高程而言,绝大部分点的拟合高程与四等水准高程的较差是个不确定值,总是在四等水准高程左右摆动,这充分说明,应用平面拟合法求均值的方法进行高程拟合,能够很好消除高程异常变化剧烈而引起高程异常不确定所带来的误差,而且选择的拟合方案越多,其效果越明显。这说明,如果高程拟合的区域不大,点位选择适当,高程拟合方案较多(10种左右),应用平面拟合法求均值的结果完全可以达到四等水准的水平。
[1] 魏二虎,黄劲松编.GPS测量操作与数据处理.武汉:武汉大学出版社,2004
[2] 北京合众合拓普科技发展有限公司.TOPCON/JAVAD GPS测量系统工程测图放样软件操作手册.
[3] CJJ73_97.全球定位系统城市测量技术规程.
A Discussion of Converting a GPS Height Into a Normal Height by Planes and Averaging
Zhang XiangPing
(Lanzhou Urban Construction Design Institute,Lanzhou 730030,China)
The attention is concentrated on the principles ang methods of converting a GPS height into a normal height by planes and averaging,then compare the consequence with converting a GPS height into a normal height and four equivalent level height by examples.
converting a GPS height into a normal height;planes;averaging
1672-8262(2011)01-73-03
P228
B
2010—03—17
张想平(1974—),男,工程师,从事工程测量工作。

