软件无线电信道处理中FIR滤波器设计研究
庞爱茹
(南昌大学信息工程学院,江西南昌330031)
1.引言
软件无线电[1]被看成是无线通信领域继模拟到数字、固定到移动的第三次革命。它使得无线通信新系统、新产品的开发将逐步转到软件上来,系统的升级基于软件,代价小,同时不同系统容易兼容和互联。
软件无线电具有极好的应用前景,例如3G中采用智能天线技术(smart antenna)、多用户检测技术(MUD)等,使软件无线电技术在3G系统中有着广泛的应用空间。在4G众多关键技术中,软件无线电技术是通向未来4G的桥梁。
软件无线电中实现对不同信道的信号接收是十分重要的工作。而数字信号处理技术[2]是这项工作的基本技术,它对软件无线电的实现是至关重要的。本论文采用数字信号处理技术对软件无线电信道处理进行了研究,提出了软件无线电中信道处理中FIR滤波器的设计研究。
2.软件无线电技术概述
2.1 软件无线电的概念
软件无线电的基本思想[1]是以一个通用、标准、模块化的硬件平台为依托,通过软件编程来实现无线电台的各种功能,从基于硬件、面向用途的电台设计方法中解放出来。功能的软件化实现要求减少功能单一、灵活性差的硬件电路,尤其是减少模拟环节,把数字化处理(A/D和D/A变换)尽量靠近天线。
2.2 软件无线电基本结构
软件无线电可分为三大组成部分,其组成部分如图1。
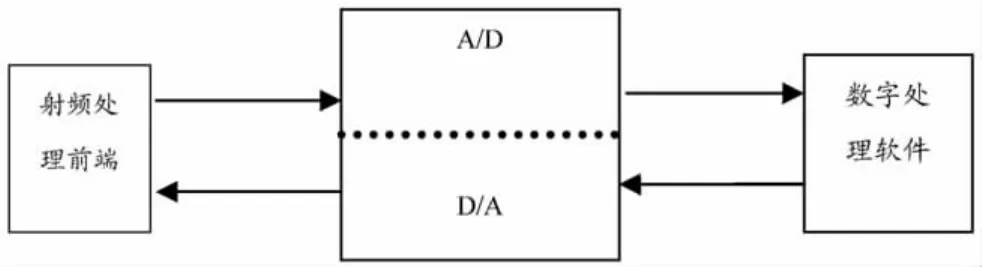
图1 软件无线电的组成部分
基于采样方式的不同,软件无线电的组成结构可以分成以下3种:
1)射频全宽带低通采样软件无线电结构(如图2);
2)射频直接带通采样软件无线电结构(如图3);
3)宽带中频带通采样软件无线电结构(如图4)。
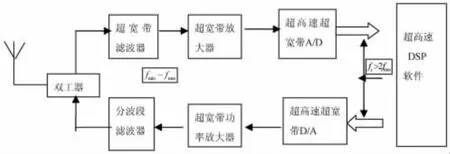
图2 射频全宽带低通采样软件无线电结构

图3 射频直接带通采样软件无线电结构
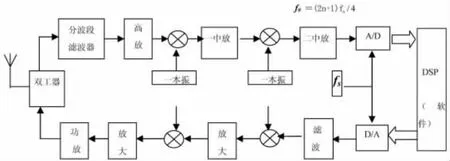
图4 宽带中频带通采样软件无线电结构
2.3 软件无线电接收机的数学模型
软件无线电接收机比较复杂,下面介绍两种接收机数学模型。
1)单通道软件无线电接收机数学模型
如图5是其数字混频法的实现。
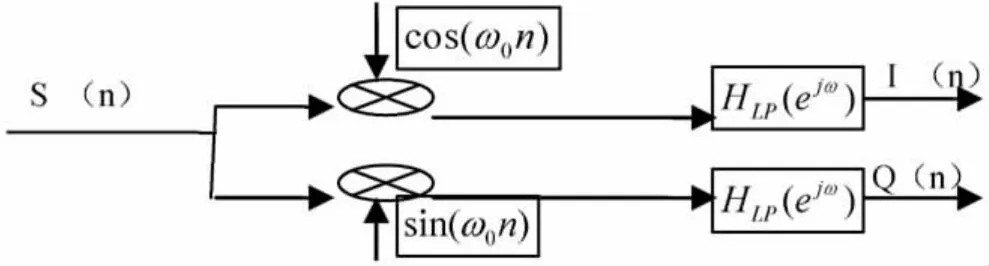
图5 单通道软件无线电接收机数字混频法实现模型
图中的低通滤波器主要用来滤除I(n)和Q(n)频谱分量以外的不需要的信号。低通滤波器的通带截止频率应为I(n)和Q(n)频谱分量中对应的最高频率,而滤波器的阻带截止频率应小于信道间隔的一半,以消除邻道干扰的影响。
2)并行多通道软件无线电接收机数学模型
通常,软件无线电采用宽带带通采样,采样的数据包含多个信道的信息,如何同时处理这些信息?因此提出并行多通道软件无线电接收机,其数学模型如图6所示。
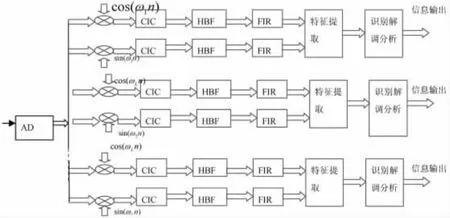
图6 并行多通道软件无线电接收机数学模型
3.软件无线电信道处理中FIR滤波器的设计
3.1 软件无线电信道处理中选用FIR滤波器的必要性
通常,软件无线电采用宽带带通采样,采样的数据包含多个信道的信息,要同时处理这些信息就要用到并行多通道软件无线电接收机,而在此接收机中要处理不同信道的信息,其中的关键技术在于构建不同频段的数字滤波器。
对于数字滤波器,一般可分为FIR(有限长单位脉冲响应)滤波器和IIR(无限长单位脉冲响应)滤波器。它们具有不同的特点,在工程中就要实际正确选用,王世一[3]和丁玉美[4]都曾对这两类滤波器进行了较详细的比较。
下面对IIR和FIR滤波器作一简单比较:
1)IIR滤波器可用较低的阶数获得高选择性,但这是以相位的非线性为代价的。相反FIR滤波器却可以得到严格的线性相位,但阶数比IIR滤波器高五到十倍。
2)FIR滤波器可以用非递归方法实现[5],误差比IIR滤波器要小得多。IIR滤波器必须注意稳定性问题。再者,FIR滤波器运算速度快得多。
3)IIR滤波器计算工作量比较小,对计算工具要求不高。大多数设计FIR滤波器的方法都需要借助计算机辅助设计。
3.2 FIR滤波器的设计思想
通过上面的分析可知,软件无线电信道处理模型中为一组FIR滤波器,而对于数字信号处理中的FIR滤波器设计而言,不管FIR滤波器数量多少,其算法都是相同的。
FIR滤波器的设计问题在于寻求一系统函数H(Z),使其频率响应H(ejω)逼近滤波器要求的理想频率响应Hd(ejω),其对应的单位脉冲响应hd(n)。
FIR滤波器的设计都要基于一定的性能指标,有窗函数设计法、频率采样设计法和最优化设计法等多种设计方法。下面介绍用窗函数设计FIR滤波器的基本方法。
设计思想:从时域从发,设计h(n)逼近理想hd(n)。设理想滤波器Hd(ejω)的单位脉冲响应为hd(n)。以低通线性相位FIR数字滤波器为例。

hd(n)一般是无限长的,且是非因果的,不能直接作为FIR滤波器的单位脉冲响应。要想得到一个因果的有限长的滤波器h(n),最直接的方法是截断h(n)=hd(n)w(n),即截取为有限长因果序列,并用合适的窗函数进行加权作为FIR滤波器的单位脉冲响应。按照线性相位滤波器的要求,h(n)必须是偶对称的。对称中心必须等于滤波器的延时常数,即

用矩形窗设计的FIR滤波器的幅度函数在通带和阻带都呈现出振荡现象,且最大波纹大约为幅度的9%,这个现象称为吉布斯(Gibbs)效应。为了消除吉布斯效应,一般采用其他类型的窗函数。
3.3 FIR数字滤波器的MATLAB设计
MATLAB信号处理工具箱提供了各种窗函数、滤波器设计函数和滤波器实现函数,楼顺天[6]等提出了MATLAB在系统分析与设计的具体方法,从中可见MATLAB对于系统分析与设计具有重要意义。
本文将针对一个含有0.2Hz、0.5Hz和0.8Hz的混和正弦波信号,设计一个FIR带通滤波器,参数要求:
通带边缘频率:ΩP1=0.45π,ΩP2=0.65π,通带峰值起伏αP≤1[dB]:。
阻带边缘频率:ΩS1=0.3π,ΩS2=0.75π,最小阻带衰减:αS≥40[dB]。
设计及滤波程序如下

其运行结果如图7、图8所示。
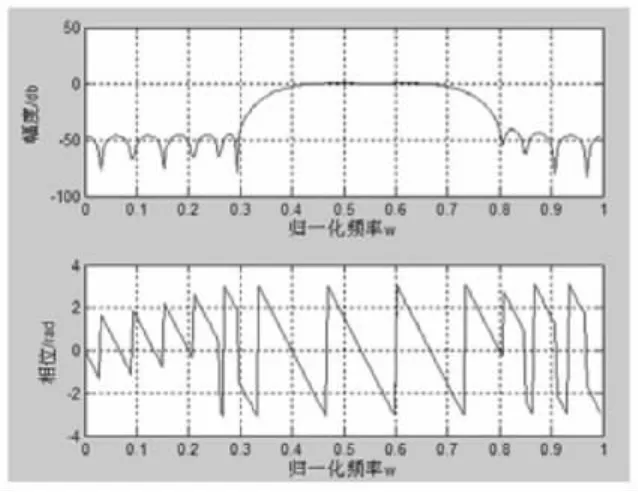
图7 滤波器幅频特性和相频特性
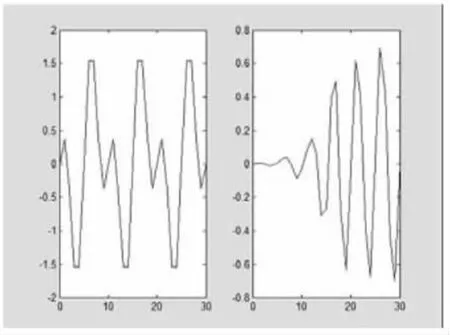
图8 滤波前后的波形
由图8可以看出,带通滤波器使输入信号s中频率为0.5hz的正弦波信号通过,而将频率为0.2hz和0.8hz的正弦波信号大大衰减。
由于MATLAB具有强大的接口功能,仿真后的结果可以很方便的移植到DSP、CPLD或FPGA等器件中。在实际应用中,只需按要求修改滤波器参数,并对程序作较少的改动,即可实现不同截止频率的FIR滤波器,实用性较强。
4.结束语
软件无线电提高了业务质量和信道接入灵活性,减轻了对硬件资源的要求。因此注定要在无线电通信领域中大放异彩。而随着超大规模集成电路技术和计算机技术的飞速发展,数字信号处理技术在软件无线电中的应用也越来越广泛,运用数字信号处理技术可方便地对接收频段、调制解调方式、滤波器特性等进行编程控制,极大地提高了通信设备的性能和设计的灵活性。而MATLAB的数字信号处理工具箱包含了各种经典和现代的数字信号处理技术,所以在实际软硬件模拟系统之前,可以先根据工程实际的需要,选择MATLAB中的窗函数来求得滤波器的系数,并编写相应的程序来检验所求得的系数是否符合最终的要求,以此来缩短设计周期,减少工作量,提高设计效率。
[1]杨小牛,楼才义,徐建良.软件无线电原理与应用[M].北京:电子工业出版社,2001.
[2]胡广书.数字信号处理:理论、算法与实现[M].北京:清华大学出版社,1997.
[3]王世一.数字信号处理(修订版)[M].北京:北京理工大学出版社,2006.
[4]丁玉美.数字信号处理[M].西安:西安电子科技大学出版社,2001.
[5]程佩青.数字信号处理教程[M].北京:清华大学出版社,2003.
[6]楼顺天,李博菡.基于MATLAB的系统分析与设计[M].西安:西安电子科技大学出版社,2001.

