模糊自适应PID控制器在水轮机调节系统中的应用

李 均

（中国南方电网调峰调频发电公司海南抽水蓄能电站项目部，海口 570105）

水轮机调节系统是一个集水力、机械、电气为一体的复杂的闭环自动调节控制系统［1］。水轮机调节系统的基本任务是根据电力系统负荷的变化不断调节水轮发电机组的有功功率输出，并维持机组转速（频率）在规定的范围内。水轮机调速器作为水电站机组主要控制设备直接影响到电力系统的安全、经济和优质运行，而水轮机调速器的性能主要取决于硬件平台以及所选用的控制策略。对于一个确定时段而言，硬件平台的选择往往受到当时技术水平的限制，因此选择合适的控制策略，充分利用调速器硬件资源是提高水轮机调速器控制性能的首要途径。

1 模糊自适应PID控制

PID控制是最早发展起来的控制策略之一，由于其算法简单、鲁棒性强和可靠性高，被广泛应用于过程控制和运动控制中，也是目前水轮机调速器中使用最广泛、技术最成熟的一种控制策略。但由于水轮机调节系统的时变、非线性特性，当水头、负荷、转速等偏离额定点时，模型的参数会发生变化，因此使用常规PID控制方式难以保证系统在所有工况都具有良好的特性，甚至可能在某些工况下还会出现不稳定现象。

针对常规PID控制存在的不足，本文拟采用模糊自适应PID控制方法，根据水轮机调节系统实际，自主设计了模糊自适应PID控制器。模糊控制的优点就是不要求掌握受控对象的精确数学模型，而是根据人工控制规则或最佳的实验实时过程来组织控制决策表，然后由该表决定控制量的大小。将模糊控制和PID控制两者结合起来，扬长避短，使其既具有模糊控制灵活而适应性强的优点，又具有PID控制精度高的特点。这种Fuzzy-PID复合型控制器，对复杂控制系统和高精度伺服系统都具有良好的控制效果。

1.1 模糊自适应PID控制原理

模糊自适应PID控制（FAPID）是用模糊数学的基本理论和方法，把规则的条件、操作用模糊集表示，并把这些模糊控制规则作为知识存入计算机知识库中，然后计算机根据控制系统的实际响应情况，运用模糊推理，即可自动实现对PID参数的最佳调整。

模糊自适应PID控制器，结构如图1所示，由两部分构成：模糊控制器和PID控制器。

模糊控制器以偏差e和偏差变化ec作为输入，运用模糊推理得到PID控制器三个预整定参数即 kp、 ki和 kd的修正参数 kp′，ki′和 kd′，通过对PID控制器的三个参数进行在线修改就可以满足不同偏差e和偏差变化ec对控制参数的不同要求，从而使被控对象具有良好的动、静态特性。

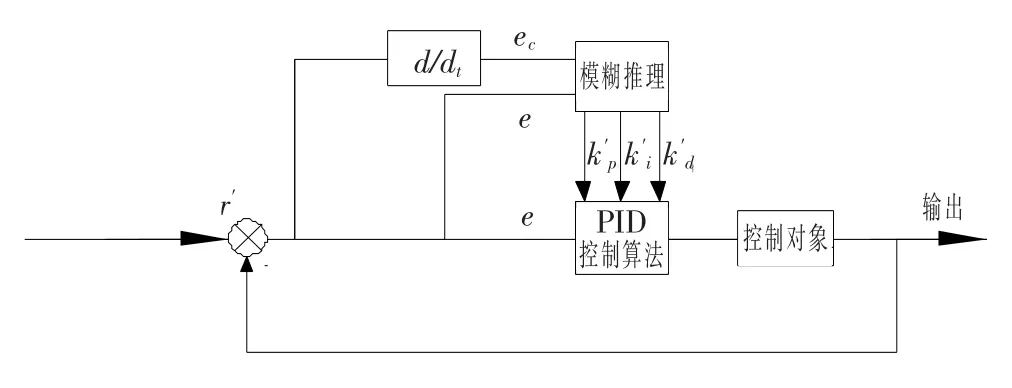
图1 模糊自适应PID系统结构

1.2 模糊自适应PID控制器的设计

1.2.1 预整定PID参数的确定

确定PID控制器的预整定参数的目的主要有以下两方面：确定模糊自适应PID控制参数变化的范围；通过对预整定PID参数的优化，为研究模糊自适应PID控制器的性能提供合适的比较对象。本文根据国内陈村水电站实际数据，确定预整定PID参数kp、 ki和kd。

1.2.2 模糊PID参数整定器的设计

确定模糊控制器的结构也就是确定模糊控制器的输入变量和输出变量（即控制量），本文采用一个二输入三输出的Mamdani模糊推理系统，结构如图2所示：

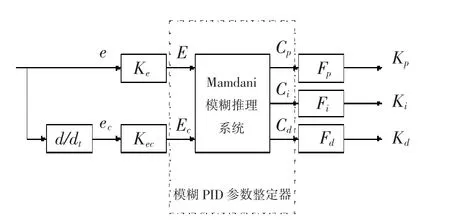
图2 模糊PID参数整定器结构框图

1.2.3 模糊控制规则的优化

控制规则的设计是设计模糊控制器的关键，常规模糊控制器的控制规则往往是从操作者的经验中提取的，因此在建立控制规则时往往需要大量的试验，耗费大量的时间，而且效果得不到保证。鉴于如上所述的缺陷，本文采用 PSO［2］（Particle Swarm Optimization）算法生成控制规则。

（1）控制规则的编码

运用计算机程序进行分析计算，首先需要将所研究的问题用数字方式进行描述，也就是编码。本文所设计的模糊推理系统共有25条规则，由于系统有三个输出量（Cp、Ci、Cd），所以编码的总长度（即PSO算法中的向量长度）将达到25×3＝75，这样需要寻优的规则太多，无疑会大大增加PSO算法寻优的计算量（时间）。下面对水轮机调节系统进行分析，在此基础上对需要寻优的规则的数量进行精简。通过过频率扰动下水轮机调速系统的响应曲线与PID参数变化规律的分析可以精简需要寻优的规则的数量。水轮机调节系统的频率扰动响应曲线如图3所示：

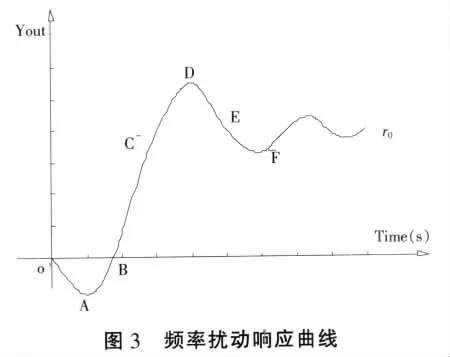
图3中，频率扰动响应曲线根据偏差和偏差的变化率可以分为OA，AB，BC，CD，DE，EF等几段。以新的平衡位置为参考，先不考虑偏差值和偏差变化率值的大小，仅考虑符号，可以发现CD与OA、EF是对称的，CD段偏差为负，偏差变化率为负，OA与EF段偏差为正，偏差变化率也为正。此时，系统的响应过程均是远离系统的平衡位置，只是偏离的方向不同而已，若偏差的绝对值和偏差变化率的绝对值相同，那么对PID三个参数的调节过程应该是完全相同的，即PID参数调整使系统逐渐靠近新的平衡位置。利用PID参数调节时所具有的对称性，可以对需要寻优的规则数进行精简。每个输出变量的规则数可以由25条减至15条，这样编码的总长度就可以缩短至3×15＝45，大大缩小了寻优的空间。

（2）模糊推理系统C语言实现

模糊推理系统的实现是仿真程序的核心，为了使利用MATLAB模糊逻辑工具箱开发的模糊推理系统能够独立于MATLAB环境，MATLAB模糊逻辑工具箱提供的两个C语言源文件fismain.c和fis.c可以实现C语言环境下对模糊推理系统的功能调用。通过两个文件中的函数调用可以读取模糊推理系统的磁盘文件，并读取输入数据文件来执行模糊推理。本文在这两个C语言源文件的基础上编写了独立于MATLAB环境的C语言应用程序来实现模糊推理系统。此外为实现模糊控制规则的优化，需要访问fis->rule_list[][]数组动态修改模糊控制规则。有关函数及数据结构的详细信息参见文献［3］。

2 仿真分析

下面就以国内安徽省陈村水电站为例，电站的基本参数如下：水流惯性时间常数Tw=0.805s，机组惯性时间常数Ta=5.72s，接力器时间常数Ty=0.3s。机组在某工况点运行的参数见表1。

表1 机组在某工况点运行的参数

取Tb=0.24·Ta=1.37，eg=0.5，则被控对象的数学模型为：

采用SIMULINK仿真比较模糊自适应PID控制器和常规PID控制器在2.5HZ频率扰动下的动态性能。利用MATLAB6.5中的模糊逻辑工具箱建立模糊系统的仿真模型，在模糊编译窗口中进行输入输出变量以及隶属度函数的设定，在模糊规则编辑器中设定经优化的控制规则，最后利用SIMULINK模糊工具集中的Fuzzy Controller组件将建立的模糊控制系统导入仿真模型中，实现与被控系统的无缝连接。模糊自适应PID控制器仿真框图如图4所示。

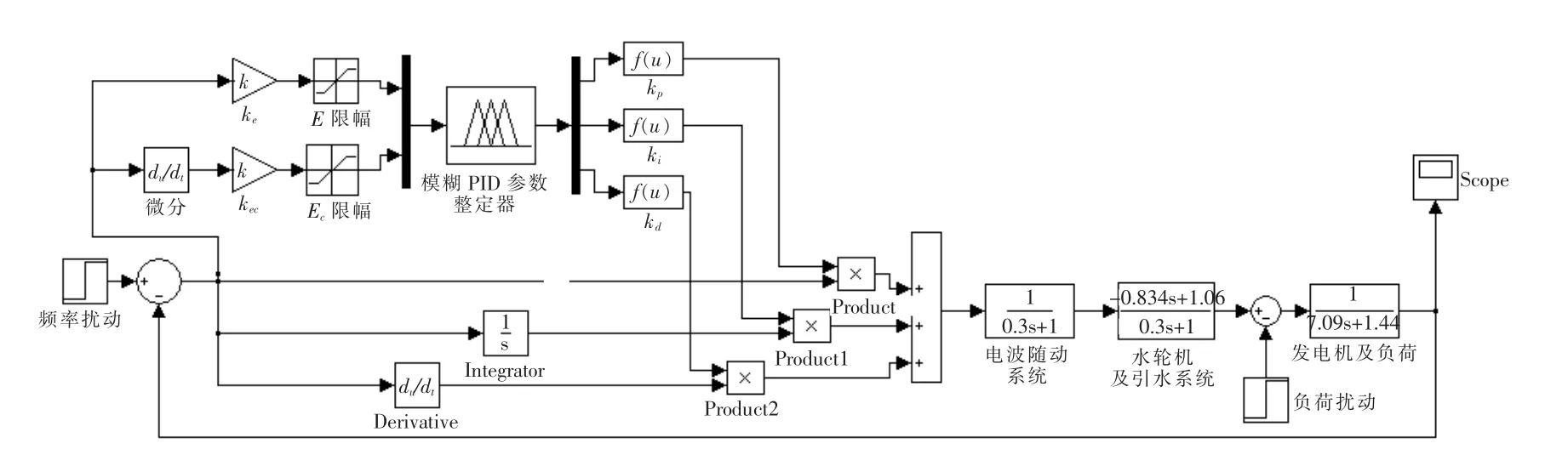
图4 模糊自适应PID控制器仿真框图

2.1 优化工况下的仿真结果分析

对水轮机调节系统施加2.5HZ的频率扰动，分别记录采用模糊自适应PID控制与常规PID控制的水轮机调节系统在优化工况下的频率响应曲线如图5所示（虚线为常规PID控制器，实线为模糊自适应PID控制器）：

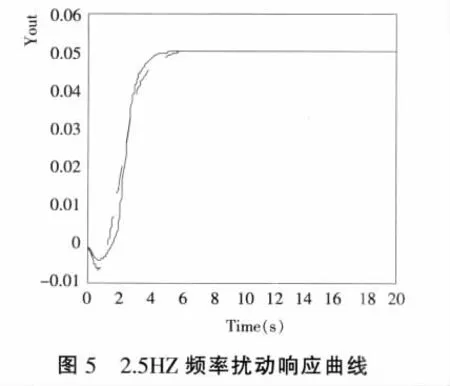
经过PSO算法优化的常规PID控制器的瞬态响应指标为：上升时间tr＝3.94s，最大过调量MP＜2%，最大下调量Mu=14%，调整时间ts=5s（稳态误差以2%计），而采用PSO优化规则的模糊自适应PID控制器的瞬态响应指标为：上升时间tr＝3.45s，最大过调量MP＜2%，最大下调量Mu=11%，调整时间ts=4.1s（稳态误差以2%计），显然模糊自适应PID控制器具有更好的动态性能。

2.2 工况变化时的仿真结果分析

为了比较模糊自适应PID控制器与常规PID控制器对工况变化的敏感程度，在以下的对比实验中将对不同工况下的频率扰动响应情况进行仿真研究。

以陈村水电站为例，取四种不同工况，由给定数据计算得到机组在不同工况点运行的参数见表2：

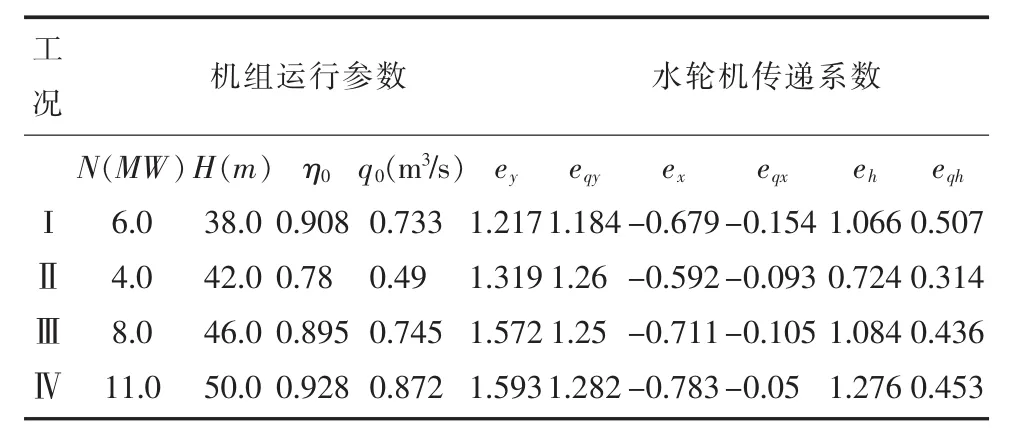
表2 不同工况点的运行参数

对水轮机调节系统施加2.5HZ的频率扰动，分别记录采用模糊自适应PID控制与常规PID控制的水轮机调节系统在四种不同工况下的频率响应曲线如图6、7、8、9所示 （虚线为常规PID控制器，实线为模糊自适应PID控制器）：

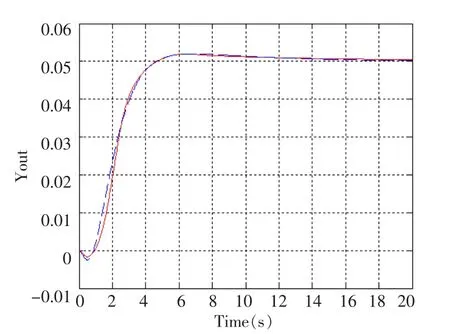
图6 工况Ⅰ 2.5HZ频率扰动响应

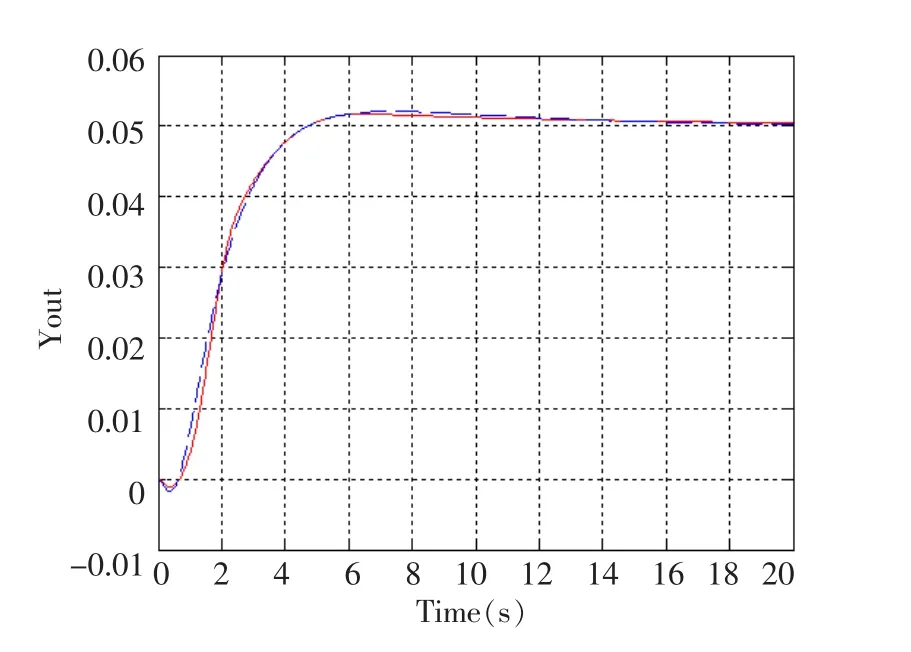
图7 工况Ⅱ 2.5HZ频率扰动响应

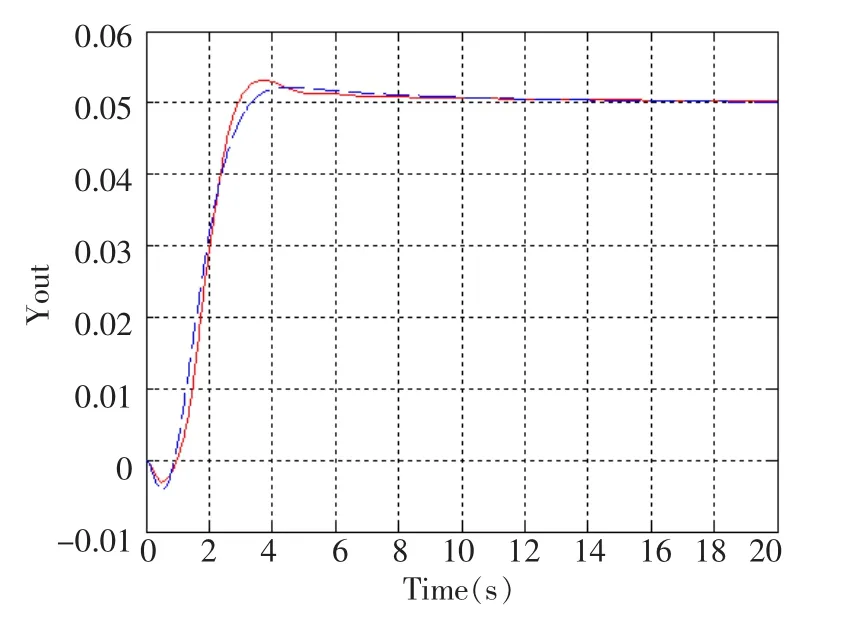
图9 工况Ⅳ 2.5HZ频率扰动响应

模糊自适应PID控制器和常规PID控制器的各项动态性能指标对比见表3。

从表3中可以看出，与常规PID控制器相比，当工况发生变化时，模糊自适应PID控制上升时间均小于常规PID控制，超调量和调整时间亦小于常规PID控制，因此模糊自适应PID控制效果明显优于常规PID控制。

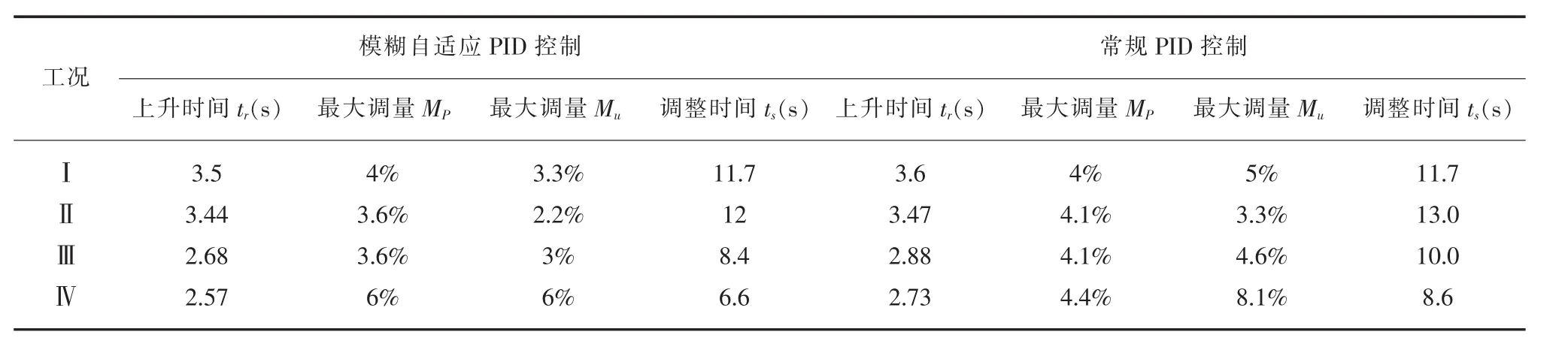
表3 2.5HZ频率扰动时的动态指标对比表

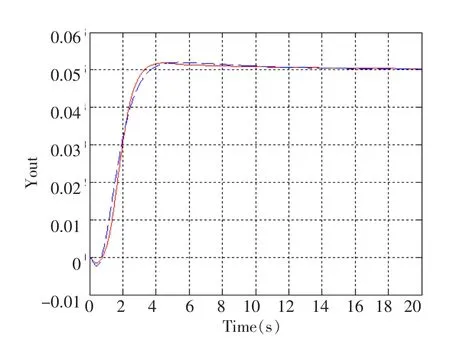
图8 工况Ⅲ 2.5HZ频率扰动响应

3 主要结论

上述仿真对比试验表明，采用经过规则优化的模糊自适应PID控制器，不仅可以在优化工况下达到比优化PID控制更好的控制效果，而且当被控对象的模型参数发生变化时，模糊自适应PID控制器仍然保持了较好的控制效果，具有较强的鲁棒性。因此，对水轮发电机组这类时变、非线性的复杂系统而言，将模糊自适应PID控制器应用到调速器的控制算法中，初步验证可以较好地改善控制系统的性能，用于实际生产还有待进一步验证。

[1]沈祖诒.水轮机调节[M].北京：水利水电出版社，1998.

[2]方红庆，沈祖诒.基于改进粒子群算法的水轮发电机组PID调速器参数优化 [J].中国电机工程学报，2005，25（22）：120-127.

[3]吴晓莉等.MATLAB辅助模糊系统设计[M]，西安：西安电子科技大学出版社，2002.