联合卡诺图在时序逻辑电路设计中的应用

卢容德 （长江大学电子信息学院，湖北 荆州434023）

时序逻辑电路经典的设计方法——驱动表法，是在完成状态编码的工作后，根据编码后的状态转换图和选择的触发器类型，列出对应的驱动表，再根据驱动表写出驱动函数和输出函数的卡诺图，用卡诺图化简法得出最简的驱动函数和输出函数表达式，得出设计电路。然后根据电路中各触发器的次态方程，用计算法求出电路无效状态的次态，检查电路是否具有自启动功能。如果电路不能自启动，还要适当修改设计，最后完成电路的设计任务[1-3]。这种方法在驱动函数的确定和自启动功能的检验等方面，使用起来都显得比较繁琐。采用次态卡诺图法，直接根据分离的次态卡诺图得出最简的次态函数，再根据次态方程确定驱动函数，可以使确定驱动函数的过程简化，但仍然不能改善自启动功能检验的不足[4-5]。为此，笔者直接根据次态联合卡诺图确定次态函数，提出了异步时序逻辑电路设计的驱动函数法和翻转模式法，并举例说明次态联合卡诺图在同步和异步时序逻辑电路设计中的应用。

1 同步时序电路的设计

1.1 设计方法

联合卡诺图设计法与经典的设计步骤完全相同，其不同点是直接根据次态联合卡诺图确定最简次态函数。文献[6]指出，时序逻辑电路的次态联合卡诺图，既是1个二维的状态转换表，又是1个表格式的状态转换图。所以，按照经典的设计方法，只要完成了状态编码的工作，就可以直接得出次态联合卡诺图。所以，采用次态联合卡诺图的同步时序逻辑电路的设计步骤为：①逻辑抽象，得出描述对象过程的原始状态转换图；②状态化简；③状态赋值，也叫状态编码；④作出次态联合卡诺图；⑤确定触发器，直接用次态联合卡诺图得出最简次态函数，在化简的过程中同时考虑自启动的问题；⑥将次态函数与触发器的特性方程相比较，确定各触发器的驱动函数；⑦根据输出要求确定输出函数；⑧画出逻辑电路。

1.2 设计举例

以文献[4]讨论的例题为对象，说明联合卡诺图在同步时序逻辑电路设计中的应用，设计1个带有进位输出的同步13进制加法计数器，要求电路具有自启动功能。

本例为计数器的设计，故直接进入同步时序逻辑电路的设计步骤③。按照8421码编码，得出13进制加法计数器的状态转换图，如图1所示。图1中，C为进位信号。

图1 13进制加法计数器状态转换图

根据状态转换图，可以得出13进制加法计数器的次态联合卡诺图，如图2（a）所示。为了使卡诺图清晰可辨，图2中没有标出输出函数。如果对8421码加法计数器的状态编码比较熟悉，可以不用状态转换图，直接写出次态联合卡诺图。

图2 例1的次态联合卡诺图

选用JK触发器实现电路的功能时，根据图2（b）中的卡诺圈，确定最简次态函数如下：

画卡诺圈时，不能将次态函数对应的现态变量消去。如化简Q3的次态函数时，不得利用无关项m15。根据卡诺图中无关项圈了为1，不圈为0的规则，很容易判别该设计是否具有自启动功能。根据图2（b），无效状态1101、1110、1111的次态分别为0010、0010、0000，电路能自启动，故可以根据上述次态方程确定驱动函数。

根据状态转换图不难得出进位信号表达式（即输出函数）：

由此得到满足设计要求的8421码同步13进制加法计数器逻辑电路，如图3所示。文献[6]将已经作出的联合卡诺图拆开，再用卡诺图法求出最简次态函数表达式。检验自启动功能时，将无效状态对应的编码代入次态函数表达式中计算次态，每个无效状态要计算4次，而根据联合卡诺图检验自启动，无需计算，因为次态联合卡诺图完整地描述了现态与次态的转换关系。

图3 同步13进制加法计数器逻辑电路图

2 异步时序电路的设计

2.1 设计方法

异步时序逻辑电路的联合卡诺图设计法与同步时序电路基本相同，其不同点在于触发器时钟信号的确定及由此产生的次态方程描述方式的变化。

与同步时序逻辑电路相比，异步时序逻辑电路的设计比较困难，但实现同一个逻辑功能，异步型时序电路比较简单。采用次态联合卡诺图进行异步时序逻辑电路设计，其过程十分简捷。

描述异步时序逻辑电路的次态方程为：

式中，Xj（j＝1，2，…，m）表示输入信号；Qi（i＝1，2，…，n）表示第i个触发器的现态表示第i个触发器的次态。

式（4）揭示了如下2个基本关系：①无CP时（CP＝0），触发器的次态保持原来的状态不变。②有CP时（CP＝1），触发器的次态由电路的输入信号和现态的组合以及触发器的特性方程决定。因而上述次态方程是异步时序逻辑电路联合卡诺图设计法的理论基础。

设计异步时序逻辑电路的方法包括驱动函数法和翻转模式法。

驱动函数法的要点是在完成状态编码工作后，首先作出次态联合卡诺图，再确定各触发器的时钟脉冲，然后写出卡诺图中时钟有效区内电路的次态函数，最后将次态函数与触发器的特性方程相比较，得出驱动函数的表达式，在时钟有效区内，该方法与同步电路设计过程相同。

翻转模式法的要点是在作出次态联合卡诺图后，首先圈出各次态的变化区（即翻转区），再确定满足驱动各触发器的时钟脉冲。按该种方法设计，触发器工作在“翻转”（即计数）方式，故驱动电路简单。

驱动函数法是先确定CP，然后求驱动函数，而翻转模式法是先确定驱动函数（即按照翻转模式驱动），然后求CP。

例如，在图4（a）所示的次态联合卡诺图中，Q0的负跳区完全覆盖Q2的变化区，在Q0的负跳区外，Q2的次态不变。如果采用驱动函数法，则Q2可以选择负边沿触发的触发器，将Q0作为Q2的CP；如果采用翻转模式法，则只需在Q2的翻转区选择CP。下面用负边沿触发的JK触发器来加以说明。

采用驱动函数法时，取CP2＝Q0，Q2次态函数的卡诺圈如图4（b）所示。在画卡诺圈时，要注意以下2点：①在CP有效区内见“1”必圈；②在CP有效区外，所有最小项都是无关项，只要化简需要，见 “0”也可以圈。

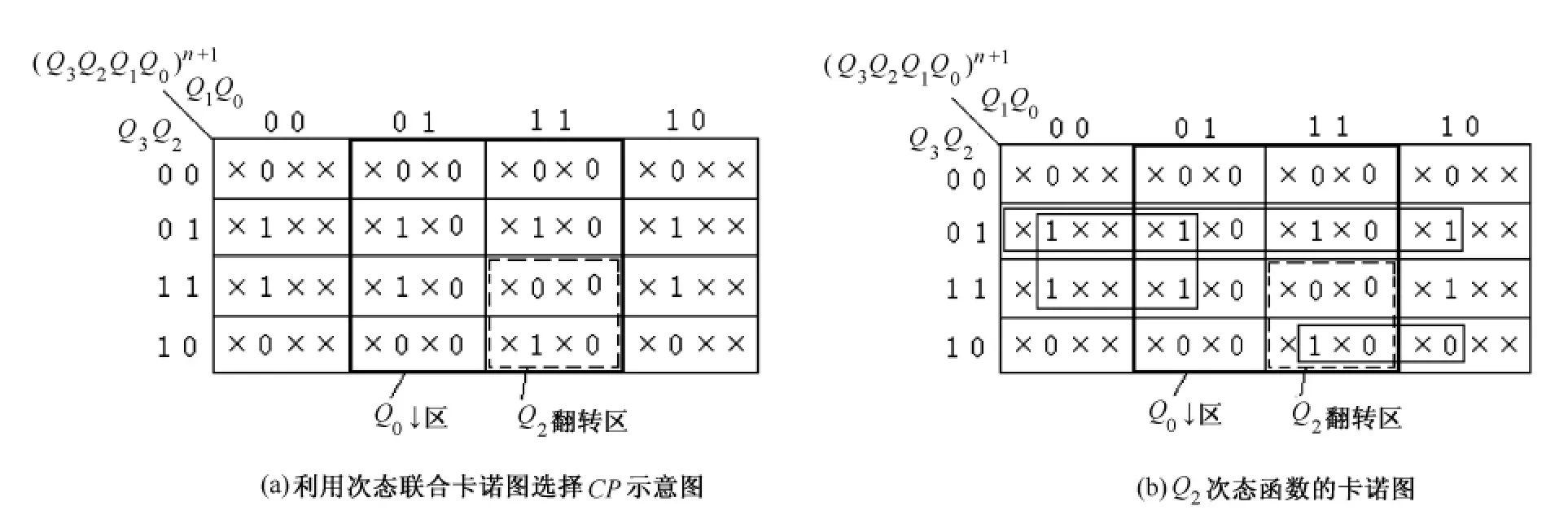
图4 次态联合卡诺图在异步时序电路设计中应用

按驱动函数法得出的Q2的次态方程如下：

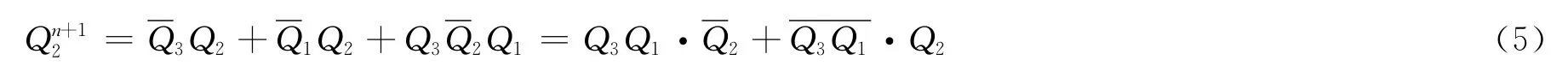
其驱动方程为：

按翻转模式法得出Q2的时钟方程如下：

其驱动方程为：

翻转模式法实际上就是CP“使能”法，即让覆盖范围较大的CP仅仅在触发器的翻转区起作用，此处就是让Q0↓ 在∑m（11，15）有效。

观察JK触发器的内部电路发现，上述2种方法设计的驱动电路完全相同，这是因为JK触发器的JK信号与CP信号就是逻辑与的关系。

异步时序逻辑电路设计中，选择CP的原则如下：①翻转最频繁的触发器用外接CP驱动，对于计数器，该触发器是电路的最低位。②高位触发器的CP由低位触发器提供，低位触发器提供的CP称为内部时钟脉冲。③当低位触发器不能满足高位触发器CP的要求时，则该高位触发器由外接CP驱动。④直接由外接CP驱动的触发器，其驱动函数确定的方法与同步时序逻辑电路的方法相同。⑤当内部时钟脉冲恰好覆盖高位触发器的翻转区时，则该触发器接成翻转模式即可。⑥当内部时钟脉冲覆盖的范围大于高位触发器的翻转区时，则该触发器的驱动设计有驱动函数法和翻转模式法。⑦内部时钟脉冲的选择，可以直接在次态联合卡诺图中用观察法确定；也可以用波形图 （时序图）进行辅助分析[4]。

2.2 设计举例

具体要求是设计1个具有自启动功能的8421码异步十进制减法计数器。

按照8421码编码后，十进制减法计数器的状态转换图如图5所示，图中，B为借位信号。其次态联合卡诺图如图6所示。

图5 例2的状态转换图

图6 例2的次态联合卡诺图

选用负边沿触发的JK触发器。首先，确定外接CP直接驱动触发器FF0，直接利用联合卡诺化简Q0的次态函数。化简时考虑到无关项，不难得出：

由于Q0工作在翻转模式，故有：

故触发器FF1驱动方程为：

接着，标出Q1的负跳区，如图7（b）所示。按照Q2在Q1的负跳区内翻转、在Q1的负跳区外保持的原则，标出Q2无效状态的逻辑值，如图7（b）所示。不难发现的负跳区恰好覆盖Q2的翻转区，故可以作为触发器FF2的时钟脉冲并且FF2工作在翻转模式，因此有：

这里，化简时利用了无关项m1。

FF3的驱动方程为：

根据状态转换图得出借位信号表达式（即输出函数）：

图7 利用次态联合卡诺图的设计过程

最后，得到满足设计要求的8421码异步10进制减法计数器逻辑电路，如图8所示。

根据图7（b）所示的次态联合卡诺图及卡诺圈，考虑的无关项的逻辑值被圈为1、未圈为0，很容易验证电路的自启动性能。完整的状态转换图如图9所示。

图8 8421码异步10进制减法计数器逻辑电路

图9 完整的状态转换图

3 结 语

设计时序电路的关键是如何确定触发器的驱动函数，使用次态联合卡诺图可以使确定驱动函数的过程简化，而驱动函数法和翻转模式法为时序电路设计的难点，它们为异步时序电路的设计提供了简便有效的方法。对于时序电路自启动功能的检查，无论涉及到同步时序电路还是异步时序电路，次态联合卡诺图法都具有其独特优势。

[1]蒋立平.数字逻辑电路与系统设计[M].北京：电子工业出版社，2008.

[2]曹汉房.数字电路与逻辑设计[M].武汉：华中科技大学出版社，2004.

[3]欧阳星明.数字电路逻辑设计[M].北京：人民邮电出版社，2011.

[4]阎石.数字电子技术基础[M].北京：高等教育出版社，2006.

[5]任骏原.基于次态卡诺图的J、K激励函数最小化方法及时序逻辑电路自启动设计[J].浙江大学学报 （理学版），2010，37（4）：425-427.

[6]卢容德.联合卡诺图在逻辑电路分析中的应用[J].长江大学学报 （自然科学版 ），2009，6（4）：N61-65.