Simpson指数和Shannon-Wiener指数若干特征的分析及“稀释效应”

许晴,张放,许中旗,贾彦龙,尤建民

（1.河北农业大学林学院,河北 保定 071000；2.河北省木兰围场国有林场管理局,河北 围场 068400）

物种多样性能够表征生物群落和生态系统的结构复杂性,体现群落的结构类型、组织水平、发展阶段、稳定程度和生境差异,具有重要的生态学意义[1-2]。所以,众多生态学家都对多样性的研究给予了极大的关注,在全球范围内针对不同的生物群落类型进行了广泛的物种多样性的评估工作[3],并相继提出了很多定量描述多样性的模型[4-7],这些模型的提出极大地推动了物种多样性的研究工作。目前来看,描述群落物种多样性的两种α多样性指数——Simpson指数和Shannon-Wiener指数能够对群落物种组成的丰富度及均匀度进行综合评价,而且数据易于获取,使用灵活、方便,因此,是目前应用最为广泛的两个数量指标。尽管对于两种多样性指数应用很广,但是对于两种多样性指数的特征及其局限性的认识并不深入,因此,在两种多样性指数的使用及解释方面存在一定的局限性。对于Simpson指数和Shannon-Wiener指数的特点,一些生态学家曾进行过论述,如马克平等[8]指出,Shannon-Wiener指数与丰富度的关系最密切,而Simpson指数则与丰富度关系较远；Simpson指数对于富集种更加敏感,而 Shannon-Wiener指数对于稀疏种更为敏感[9]。对于这些特征的论述多是从具体的研究实例出发,缺乏具体的论证,而且有的是一种定性的判断,缺乏具体的定量描述,如划分稀疏种和富集种的具体标准是什么。针对这些问题,本研究以一种假设的群落条件及情景变化为基础对两种多样性指数的特征进行分析,包括两种多样性指数与丰富度和均匀度的关系、富集种的划分标准等。希望通过这些问题的研究,促进人们对于这两种多样性指数的认识、使用和解释。

1 研究方法

1.1 多样性指数对均匀度的敏感性分析在物种丰富度不变的情况下,均匀度变化必然会使Simpson指数和Shannon-Wiener指数发生相应的变化。由于两者对均匀度的敏感性不同,在均匀度变化相同时,两种多样性指数的变化率必然有所差异。根据此原理,首先设计多个不同的群落,每个群落都含有两个物种,分别为物种1和物种2,保证每个群落的两种丰富度指数S指数和Margalef指数不变,使群落由最不均匀变化至均匀,从而达到丰富度不变、均匀度逐渐变化的目的。具体做法如下:设置50个群落,每个群落含有两个物种,假设从群落1到群落50,物种1及物种2的相对多度分别按0.99,0.98,…,0.50及0.01,0.02,…,0.50的变化规律发生变化（表1）。分别计算每个群落的Shannon-Wiener指数、Simpson指数以及 Pielou（si）均匀度[7]指数值,然后,进一步计算相邻群落的均匀度指数的变化率及Shannon-Wiener指数、Simpson指数值的变化率,从变化率的高低可反映出两种多样性指数对均匀度的敏感性。计算公式如下:

Shannon-Wiener指数:

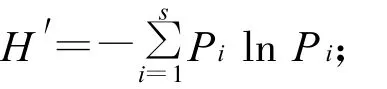
Simpson指数:

Pielou（si）均匀度指数:

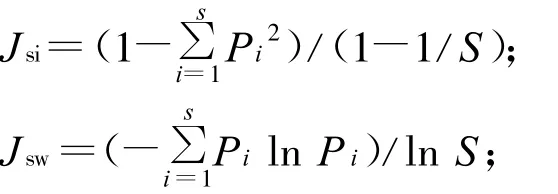
Shannon-Wiener指数的变化率:

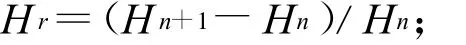
Simpson指数的变化率:

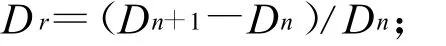
Pielou（si）均匀度指数的变化:

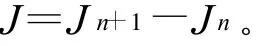
式中,n为群落编号；Hn、Dn、Jn分别为n群落的Shannon-Wiener指数、Simpson指数和 Pielou（si）均匀度指数；Jsi为基于Simpson指数计算的均匀度指数；Jsw为基于 Shannon-Wiener指数计算的Pielou均匀度指数。

表1 丰富度相同而均匀度不同的50个群落

1.2 多样性指数对物种丰富度的敏感性分析设计两个群落组A和B,每组各有15个群落（如表 2）。假设,A 组中的各群落A1、A2、A3、A4、A5…A15的物种数分别为 1、2、3、4、5…15；B 组中各群落B1、B2、B3、B4、B5 …B15的物种数分别为 30、29、28、27、26…16。同时假设,两组中的各群落所包含物种的个体数都为50（也可以是其他数值）,以保证各群落的均匀度都相等（均匀度都为1）。分别计算两组中各群落的 Simpson指数和 Shannon-Wiener指数。然后,分别计算A组中各群落与B组中相应群落的丰富度及两种多样性指数的差值和变化率,以此考察在均匀度不变的情况下,多样性指数随丰富度指数的变化率,从变化率的高低可反映出两种多样性指数对丰富度的敏感性。

Shannon-Wiener指数的变化率:

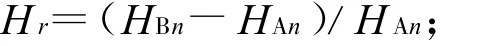
Simpson指数的变化率:

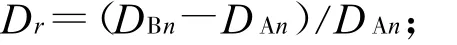
丰富度的变化:

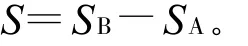
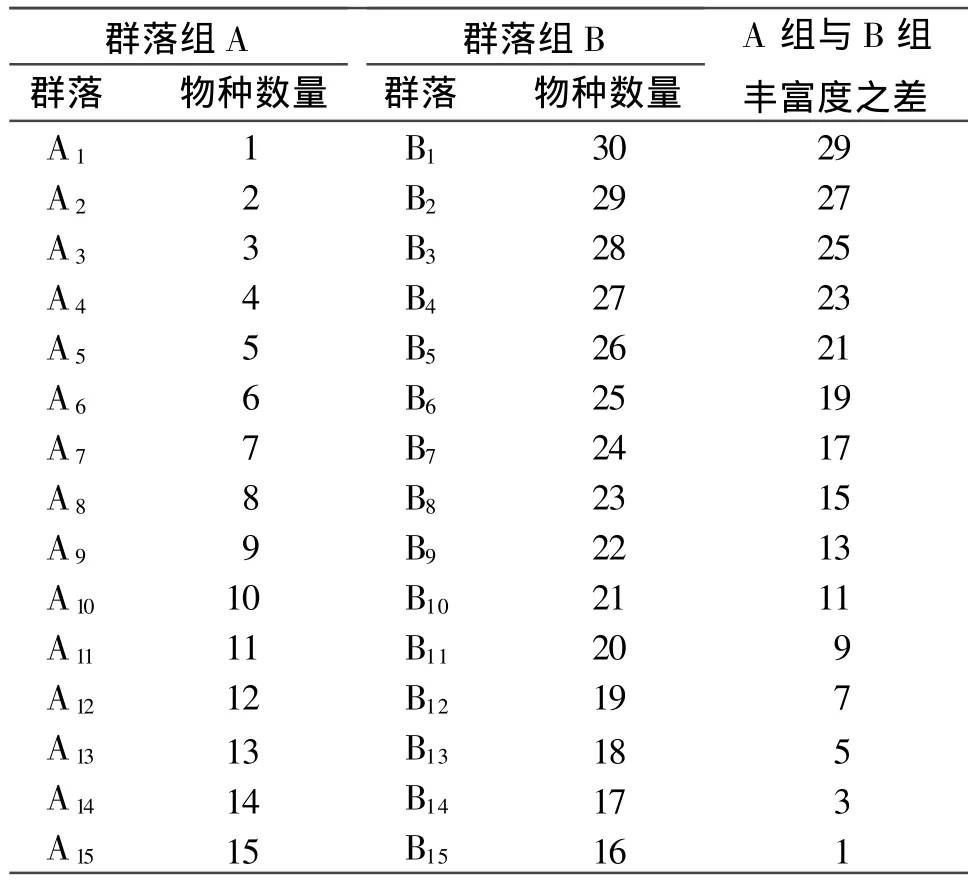
表2 均匀度相同而丰富度不同的两组群落

1.3 富集种的确定根据Magurran[9]的观点,Simpson指数对于富集种更加敏感,而 Shannon-Wiener指数对于稀疏种更为敏感,即当不断加入一个富集种时,Simpson的变化率应该大于Shannon-Wiener指数,而加入一个富集种时,Shannon-Wiener指数的变化率应该大于Simpson指数。基于这样一种认识,假设一群落含有a、b两个物种,各含有50个个体,然后引入第3个物种c,让物种c按0,1,2,…,1 000的数量逐步引入,在此过程中,物种c逐渐从稀疏种向富集种变化。在该过程中,计算每次加入物种c后,群落的Simpson指数和 Shannon-Wiener指数的变化及相对原始群落的变化率。基于Magurran[9]的观点,即:Simpson指数对于富集种更加敏感,而Shannon-Wiener指数对于稀疏种更为敏感,在物种c逐渐由稀疏种转变为富集种的过程中,在某一时刻之前,Simpson指数的变化率应该低于 Shannon-Wiener指数的变化率,而后,Simpson指数的变化率应该高于Shannon-Wiener指数的变化率,该时刻物种c的相对多度可以看作是富集种和稀疏种的划分标准。该时刻在坐标系中表现为两条多样性指数变化曲线的交点。

2 结果与分析

2.1 多样性指数对均匀度的敏感性分析在Pielou（si）均匀度指数的变化逐渐增加的过程中,Simpson指数的变化率始终大于Shannon-Wiener指数,而且随着均匀度指数变化的增加,两种指数的变化率的差值也有逐渐增加的趋势（图1）。说明在丰富度不变的情况下,Simpson指数比Shannon-Wiener指数对均匀度的敏感性更强。进一步利用清西陵地区油松林侧柏林群落的实地调查数据进行验证（表3）。侧柏林和油松林的两个样方的物种丰富度S和Margalef指数均相同,分别为8和1.27,Simpson指数变化率为0.17,Shannon-Wiener指数的变化率为0.11,前者大于后者。该结果验证了前面的结论:与Shannon-Wiener指数相比,Simpson指数对均匀度更为敏感。

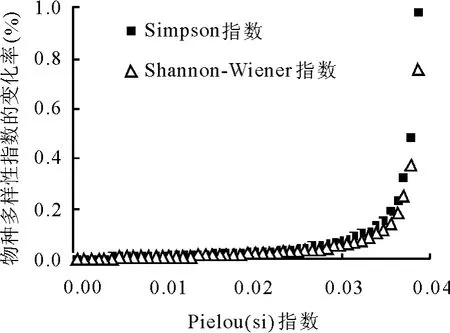
图1 Simpson指数和Shannon-Wiener指数对均匀度敏感性

表3 清西陵地区油松林和侧柏林物种多样性的比较

2.2 多样性指数对丰富度的敏感性分析随着物种丰富度S的变化值逐渐增大,Simpson指数和Shannon-Wiener指数的变化率均逐渐增大,在变化过程中,Shannon-Wiener指数的变化率始终大于Simpson指数的变化率（图2）,说明在均匀度变化程度相同的情况下,Shannon-Wiener指数的变化率高于Simpson指数,即Shannon-Wiener指数对丰富度的敏感性更强。

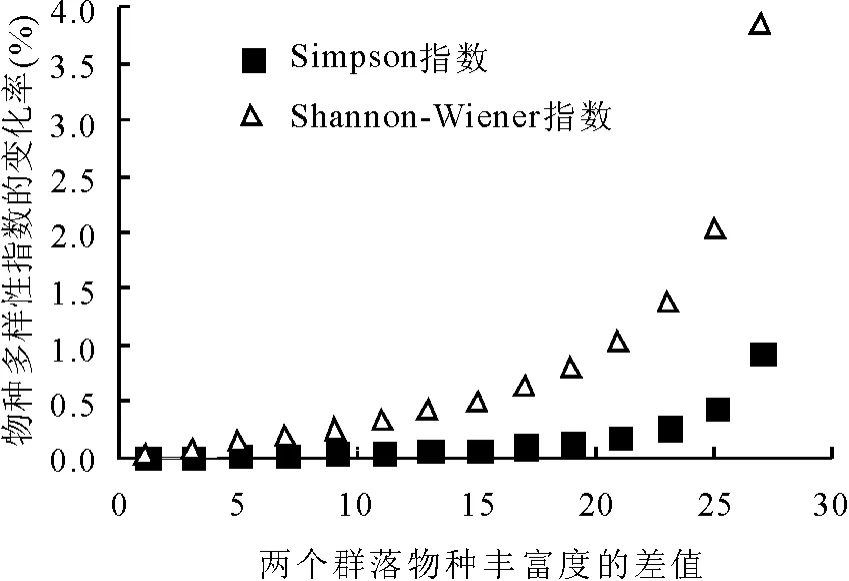
图 2 Simpson指数和Shannon-Wiener指数对丰富度的敏感性

2.3 富集种标准的确定如图3a所示,当新加入物种c的相对多度小于0.72时,Simpson指数和Shannon-Wiener指数的变化率均大于0,说明两种多样性指数均在增加,同时,Shannon-Wiener指数的变化率一直大于Simpson指数的变化率,说明在新加入物种的相对多度较低（0.72）时,Shannon-Wiener指数的变化率大于Simpson指数的变化率,即Shannon-Wiener指数对稀有种的敏感性更强,而当物种c的相对多度大于0.72时则正好相反,Simpson指数的变化率大于Shannon-Wiener指数的变化率,说明Simpson指数对富集种的敏感性更强。

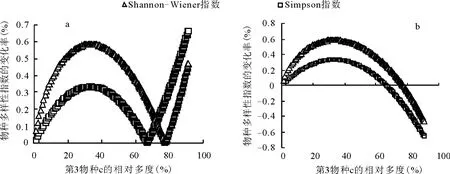
图3 随物种c相对多度的变化Simpson指数和Shannon-Wiener指数的变化率的比较

另外,笔者发现,在物种c的数量增加到一定程度以后,群落的物种多样性指数不但不增加反而会有所下降,即此时的多样性指数低于原有的未增加物种c时的多样性指数（图3b）。好像物种c的加入使群落物种多样性受到“稀释”一样,可称之为“稀释效应”,即当新增加物种的相对多度超过一定范围时,多样性指数不但不增加,反而会有所下降。对于Simpson指数来说,此时物种 c的相对多度约为0.67；对于 Shannon-Wiener指数来说,物种c的相对多度约为0.77。

3 讨论

本研究通过假设的几种简单的群落条件和物种多样性的变化情景,对两种多样性指数的几个特征进行了分析和论证。证明两种多样性指数对于物种丰富度和均匀度的敏感性是不同的,Simpson指数对于均匀度的敏感性高于Shannon-Wiener指数,而Shannon-Wiener指数对于物种丰富度的敏感性高于Simpson指数。对于这种现象,许多生态学家在研究中已经注意到了,如马克平等[8]在对北京东灵山地区植物群落多样性进行研究时也提出了多样性指数中Shannon-Wiener指数与丰富度的关系最密切,而Simpson指数和种间相遇几率则与丰富度关系较远。如陈廷贵和张金屯[10]在用关帝山89个样地植被数据对15个物种多样性指数进行比较研究时认为,受丰富度影响较大的多样性指数依次为Shannon-Wiener指数、Simpson指数,受均匀度影响较大的多样性指数依次为Simpson指数、Shannon-Wiener指数。这种现象都是从各自的具体研究结果中发现的,并未给出相应的证明,本研究通过假设的几种简单的群落条件和物种多样性的变化情景证明了这一规律具有一定的普遍性。该结论对于两种多样性指数的选择具有一定的指导意义。在对物种丰富度接近而均匀度不同的群落进行比较时,采用Simpson指数可能效果更好,而对均匀度接近、丰富度差别较大的群落进行比较时,Shannon-Wiener指数的效果更好。

另外,根据 Magurran[9]的观点,即 Simpson指数对于富集种更加敏感,而Shannon-Wiener指数对于稀疏种更为敏感,但是,他并未给出稀疏种和富集种的一个确定的判断标准。本研究通过一个简单的试验设计计算出,相对多度0.72可以看作物种是否是富集种的判断标准。即新加入物种的相对多度低于0.72时,物种为稀疏种,而大于 0.72时,该物种为富集种。最后将A、B两物种的个体数设为8、100、1 000后进行平行试验,通过计算发现,同样存在上面的特征,只是数值上稍有偏差,但都在0.72左右,故这一数值的提出是有意义的,可作为富集种的初步判定标准。

根据多样性指数的变化规律提出了“稀释效应”的概念,即在一个群落中增加新的物种时,当新增加物种的相对多度超过一定的范围时,群落的物种多样性指数不但不会增加,反而会有所下降。“稀释效应”的存在说明Simpson指数和Shannon-Wiener指数在描述群落多样性的变化时,存在一定的局限性。岳天祥等[11]也曾发现类似的现象,他指出Shannon模型变化率为0的点约为0.37,该值与本研究的0.77结果的差别较大,其原因可能是岳天祥等[11]分析的是Shannon模型H′≈-∑PilnPi中的核心函数f（x）=xlnx,忽视了模型中求和对于结果的影响。

本研究通过简单的试验设计对两种多样性指数的若干特征进行了分析,结果将有助于对两种多样性指数的认识、使用和解释。但是,其对于更复杂群落的适用性还需进一步的分析和证明。

[1]马克平.论述生物多样性的概念[J].生物多样性,1993,1（1）:20-22.

[2]赵惠勋.群体生态学[M].哈尔滨:东北林业大学出版社,1990.

[3]Faith D P.Global biodiversity assessment:integrating global and local values and human dimensions[J].Global Environmental Change,2005,15（1）:5-8.

[4]MaIntosh R P.An index of diversity and relation of certain concepts to diversity[J].Ecology,1967,48:392-404.

[5]Whittaker R H.Evolution and Measurement of species diversity[J].Taxon,1972,21:213-251.

[6]Hurlbert S H.The Non-concept of species diversity,a critique and alternative parameter[J].Ecology,1971,52:577-586.

[7]Pielou E C.Ecological Diversity[M].New York:Wiley-Interscience,1975.

[8]马克平,黄健辉,于顺利,等.北京东灵山地区植物群落多样性的研究[M].生态学报,1995,16（3）:225-234.

[9]Magurran A E.Ecological diversity and measurement[M].New Jersy:Princeton University Press,1988.

[10]陈廷贵,张金屯.十五个物种多样性指数的比较研究[J].河南科学,1999,17（增刊）:55-57,71.

[11]岳天祥,周成虎,李振清,等.生物多样性模型的理论分析[J].地球信息科学,1999,1（1）:19-25.