基于标签信息分组的射频识别防碰撞算法*
李波
(华南理工大学电子与信息学院,广东广州510640)
射频识别(RFID)技术作为一种新的自动识别技术,以其快速、实时、准确采集的特点在众多领域得到广泛应用[1-2].RFID系统主要由阅读器、标签和数据处理3部分组成,其中阅读器和标签之间采用非接触工作方式交互信息.在RFID系统中标签有3种类型:主动、被动和半主动[3-5].文中主要讨论被动类型的标签.被动标签本身是无源的,其工作所需的能量是靠阅读器传输给它的[2],且标签之间不能交互,多个标签同时发送数据会导致阅读器读取数据冲突.防碰撞算法就是用来避免这种情况的发生、协调标签之间顺序工作的.目前主要有两种防碰撞算法:二叉树算法和ALOHA算法[6-7].
ALOHA算法是标签在每个时隙开始时竞争信道,竞争到信道的标签发送数据,没有竞争到的会随机地等待一段时间后再次竞争信道[5,8].Deng等[9]提出一种可以自适应调整时隙的算法,该算法能够根据未识别的标签数量调整时隙的数量,使得识别吞吐量达到最大值.二叉树算法中,阅读器通过要求标签不断地选择0和1来使标签有序地发送数据.这两种算法虽然能解决标签的冲突问题,但交互过程过多,且随机性很强,当标签数量较多时,识别效率会严重下降[1,5,8,10-11].邓辉舫等[12]对二叉树算法进行了改进,使算法保持后退式二进制树形搜索算法的后退机理,实现标签的有序读取.在这两种算法的基础上,Wang等[13]提出了一种基于ALOHA的分组识别算法.该算法先利用循环过程来预识别所有的标签,然后将所要识别的标签进行分组,分组结束后再利用ALOHA算法识别各组中的标签.
为减少可读取标签的数量并自适应地改变标签应答时隙的数量以提高系统的识别效率,文中依据概率统计理论和代数理论提出了基于标签信息分组的防碰撞算法.
1 算法描述
电子标签是识别对象的数据承载体,存储识别对象和标签的信息,并在数据写入标签后对这些数据序列生成一个循环冗余校验(CRC)码,用于在数据通信中校验序列[14].分组识别算法就是以标签的CRC码作为分组依据.算法中利用这些已生成的CRC码再生成更低位的CRC码值作为每个标签的组号,而每个组中的标签以自身的标签序号作为随机算法的种子,生成随机数并作为它占用的时隙序号,其中每个组的时隙总数为2l,l为标签序号的位数.然后,阅读器按照分组顺序依次识别这些标签,在组内按照标签所选择的时隙号依次读取数据.
1.1 标签状态的迁移
标签在识别的过程中处于不同的状态,根据阅读器的请求命令从一个状态迁移到另一个状态.文中算法定义了标签在识别过程中的5种状态:
(1)激活状态标签选择了一个时隙,正在与阅读器进行交互.
(2)休眠状态标签已选择了时隙,在等待阅读器的唤醒请求.
(3)已识别状态标签已被成功读取,处于该状态的标签不再响应任何阅读器命令.
(4)等待状态处于该状态的标签表示该标签所在的组还没有被阅读器选中并进行识别,在等待阅读器的REQ-Start请求.
(5)冲突状态当标签所选择的时隙与其它标签相同时所具有的状态.
标签状态迁移过程如图1所示.所有的标签在识别开始时全部处于激活状态,分组结束后,没有被选择识别的组迁移到等待状态,而被选中的标签组则保持激活状态,完成时隙选择后迁移到休眠状态,直到阅读器唤醒标签开始识别.所有冲突的标签在一次轮询识别结束后响应阅读器的请求返回激活状态,重新开始选择时隙,直到被成功读取,响应REQ_Kill请求迁移到已识别状态.其它保持等待状态的标签要在被识别的组中的所有标签都迁移到已识别状态后,才会被阅读器唤醒.
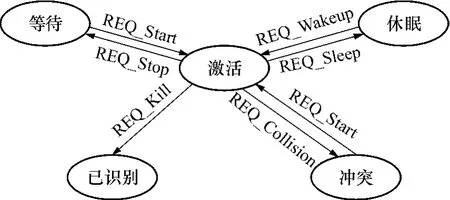
图1 标签状态迁移示意图Fig.1 Schematic diagram of state transition of tag
1.2 标签分组与时隙选择
现有的RFID标准中一般采用16位的CRC码作为校验码,故文中以16位CRC为例进行讨论.当阅读器检测到有新标签进入其射频场后,先锁定标签,并在后续识别过程中只识别这些锁定的标签,防止有新的标签进入时扰乱正在进行的识别过程.标签收到开始识别的请求后,提取自身的16位CRC码值,采用模2除法去除4位CRC码,生成多项式G(x)=x4+x+1[15],并求得4位CRC码,这样每个标签所在组即被唯一确定.4位CRC码值可表示的范围是0~15,所以所有的标签被分配到16个组中.
在识别过程中每个组有2n(2≤n≤l/2)个时隙供标签进行选择,其中n的值取决于每次轮询结束后冲突时隙、空时隙和成功读取时隙的统计结果.标签采用伪随机数生成(PRNG)算法生成一个随机数作为该标签选择的时隙号码.但要求RNG生成的随机数序列是均匀分布的,以保证标签不会过度集中地选择某个时隙.线性同余算法是一种简单可行的随机数生成算法,在参数正确设置的前提下,它所产生的随机序列分布均匀,其形式如下:

式中:r为随机数;I为随机算法的种子;λ为整数乘子;c为整数常量;m为每次轮询的时隙总数,m=2n.由文献[16-19]可知,式(1)中的参数按如下设置时所产生的随机序列具有很好的分布性:(a)λ和m互为质数;(b)如果λ-1是质数p的倍数,那么p是λ-1和m的公约数.
由于标签采用线性同余的方法产生一个随机数作为时隙号码,而不是产生一个序列,因此种子I决定了每组中标签选择时隙的分布情况.从式(1)可知,当两个标签选择的种子相同时,生成的时隙号码是相同的.文中采用标签序号作为随机算法的种子源,其中s表示种子位数,s等于本次轮询时隙总数2n的幂,则取种子步骤如下:
1)第1次轮询时,直接取标签序号的后s位作为种子;
2)在第k次轮询时,按顺序从后向前取k串s位的子串,将这k串子串的异或值作为种子;
3)若k-1,则按第1次轮询时的方法取种子.
1.3 轮询识别过程
阅读器中设置3个计数器,分别记录没有被选中的时隙(es计数器)、成功读取的时隙(ss计数器)、发生冲突的时隙(cs计数器).在轮询之前,3个计数器均初始化为0,当一次轮询结束后,阅读器可以根据这3个计数器的情况判断是否将当前组内的标签读取完毕,以及是否调整下一轮轮询中标签的可选择时隙范围.
在标签选择完时隙后,阅读器开始对这一组的2n个时隙进行轮询识别.当有标签选择的时隙与其它标签相同时,碰撞就会发生,此时阅读器不作处理,继续识别后面的时隙.所有2n个时隙识别完毕后,若有碰撞发生,则请求标签重新计算种子,然后开始下一次轮询.一次轮询算法的步骤如下:
1)发送REQ_Query请求,其中包括阅读器所要读取的时隙号码.
2)如果收到ACK_Query响应且没有冲突发生,则读取成功,转步骤3);如果收到ACK_Query响应且有冲突发生,则转步骤4);如果没有任何响应,表明该时隙没有标签被选中,则es计数器(空时隙计数器)加1,转步骤5).
3)发送REQ_Kill请求,将被成功读取的标签锁死,ss计数器(独占时隙计数器)加1,转步骤5).
4)cs计数器(冲突时隙计数器)加1.
5)阅读器中时隙计数器加1,准备读取下一个时隙,返回步骤1).
一次轮询识别结束后,阅读器根据3个计数器的结果进行估计判定,调整时隙总数,然后读取该组剩下的标签,判定准则如下:
1)如果cs计数器为0,则表示当前这一组所有标签读取完毕,准备读取下一组标签.
2)如果cs计数器不为0,有以下2种情况,其中r表示上一次轮询的时隙总数.
(a)当es=0时,若cs>ss,则表明冲突严重,若n=32则时隙总数保持不变,否则在下一次轮询时时隙总数设为2n+1;若cs≤r/2,则时隙总数保持不变.
(b)当es≠0时,若cs>es+ss,则时隙总数保持不变;若cs≤r/2且n=2,则时隙总数保持不变,否则时隙总数设为2n-1.
算法分组过程如图2所示.两种准则分别根据碰撞情况调整时隙总数,从而提高系统的识别效率.
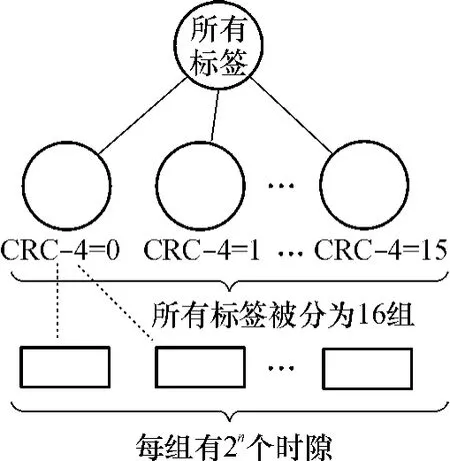
图2 分组示意图Fig.2 Schematic diagram of splitting
2 算法分析
文中算法最关键的两个步骤是标签分组和时隙选择,因为算法是基于标签自身携带的信息进行划分的,而所有的信息是不可预知的,那么所有的标签是否可以利用CRC码进行分组?在每个小组中标签是采用线性同余法选择时隙,是否会出现某个时隙无限重复被选的情况?文中分别讨论这两个问题.
2.1 分组效率问题
文中讨论分组识别算法时,以标签中携带16位CRC码为例,利用生成多项式G(x)=x4+x+1产生4位CRC码.
随机均匀地产生t个标签,令X1,X2,…,Xt分别表示它们所携带的16位CRC码,则Xi∈{0,1,…,216-1},i=1,2,…,t,且Xi以等概率取值.令RXi表示Xi对G(x)求模取得的余数,则RXi∈{0,1,…,24-1},且以等概率取值.在算法中,RXi是各个标签的分组号,因此各个标签被分配到16个组中,且被分配到其中一个组的概率相同.可见文中算法可以将所要识别的标签相对均匀地分配到16个组中.
分组过程是在标签接收到阅读器的分组命令后开始的.所有的标签接收到阅读器的分组命令后,同时开始进行除法运算产生分组号,因此所有标签的分组过程所消耗的时间等于一个标签进行除法运算的时间,即分组过程的算法复杂度相当于一次除法运算的算法复杂度.求取CRC的移位除法运算的复杂度为O(d),即分组过程的复杂度为O(d)[15],其中d为被除数的位数,在分组过程中用16位CRC产生4位CRC码,因此d为16.
2.2 时隙分配问题
由式(1)可知,若参数确定,线性同余算法产生的随机数是由种子I确定的,并且若I是周期m内的一个整数,那么产生的随机数是由种子唯一确定的.也就是说,假如一个标签采用的种子与其它标签不同,则该标签占用的时隙也与其它标签不同.假设第k次轮询时种子位数为s位,那么第k次轮询的种子是标签序号中从后向前取k个s位长的子串的异或值.

设X1和X2分别表示同一组中任意两个标签的l位长的序号(由0、1组成的混合序列),且X1≠X2,S1和S2分别是它们的种子,位数为s.设这两个标签的序号具有以下形式:

其中“×”表示一个s位子串,共有⎿l/s」个子串.X1中第i-1和i个子串分别是a和b,X2中第i-1和i个子串分别是c和d.若在前i次轮询中这两个标签产生的种子一样,由式(2)可知,X1和X2的前i个s位子串必是式(3)-(6)所示的4种形式之一,其中设两个标签的后l-si位任意取值,令和分别表示两个标签的第j个s位子串表示对子串求反,P(i)表示第i(i=1,2,3,4)种情况的概率.



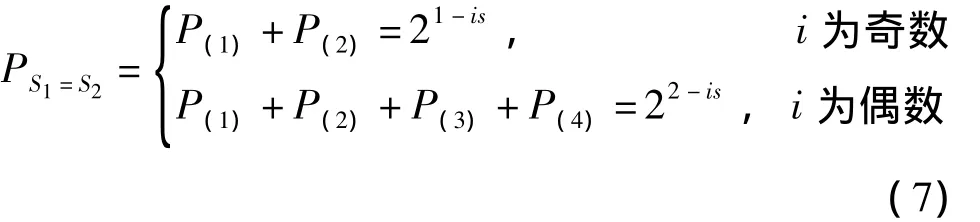
当i=n/l时,第2种情况中X1=X2,由于序号的唯一性,所以第2种情况不会导致两个标签无限地产生同样的种子;在第3和第4种情况中,由于只有当i为偶数时才有,当i为奇数时两个标签不会冲突,所以也不会导致两个标签始终产生同样的种子.
对于第1种情况,当i=l时,标签的两个序号且X1≠X2.由于第1次轮询是直接取序号的后s位作为种子,若第1次轮询时这两个标签均不能被识别,则由式(2)可以知道在后续的轮询中这两个标签产生的种子是一样的,出现无限选择同一时隙的情况,那么对于任意两个标签序号其不能被识别的概率为

文中是假设标签序号为32位进行讨论的,则PX1=¯X2=2-32.在现有的RFID标准中标签大多采用64位或更高的序号,因此不能被识别的概率更低.可以通过减少有效射频范围内标签数量的方法来避免标签无法被识别的情况发生.
3 仿真实验
是否可以识别所有的标签和识别的快慢是判断算法好坏的两个关键指标.由于仿真环境与真实的识别环境有区别,所以文中将识别过程中阅读器与标签之间发送、接收的命令数量作为判断算法识别效率的依据.文中算法利用16位的CRC码进行分组识别,因此在仿真过程中主要是利用随机算法产生均匀分布的16位数据来模拟标签中的16位CRC码.仿真用14组标签数据,标签数量逐步增加,每组标签数量为100k',k'为组号.王铖岑[5]和江岸等[7]已对ALOHA算法和二叉树算法的性能进行了比较,结果表明二叉树算法优于ALOHA算法,因此仅将文中算法与二叉树算法的性能进行对比.
从1.3节的算法步骤可知,时隙分配时初始的时隙数为2n(n与标签ID有关),在识别过程中每次轮询结束后,阅读器会根据3个计数器(es,ss,cs)来调整时隙数,那么在第1次轮询时的初始时隙数(即最小时隙)会影响算法的识别效率:若最小时隙设置偏小,则当标签数量较多时冲突时隙出现的概率较大,增加轮询的次数而消耗更多的时间;若最小时隙设置偏大,则当标签数量较少时空置时隙出现的概率较大,降低了算法的识别效率.文中仿真使用的数据标签最大达到1400个,若设置很大的初始时隙势必造成更多的空闲时隙,因此最大初始时隙设为64.文中利用上述14组标签数据对最小时隙为4、8、16、32、64时的5种情况分别进行仿真计算,结果如图3所示.
从图3中可以看到,当标签数量较少时,最小时隙较小的识别过程识别的速度较快,这是因为在标签数量较少而最小时隙较大时,空时隙的数量会比较多,此时算法在空时隙上会花费较多的时间.随着标签数量的增多,碰撞发生的概率也随之增加,所以最小时隙较小的识别过程会越来越慢.当标签数量增加到一定程度时,最小时隙大的识别过程明显地比最小时隙小的识别过程要快很多.Deng等[9]也指出了类似的情况,即在时隙数量较少时,随着标签的增加,折线发散得较快,因此在算法应用中可以根据实际情况设定最小时隙.从图3中还可以看到,不同的最小时隙需要几乎相同的命令数量,如在标签数量达到600时,最小时隙4和最小时隙8的命令数量相当.这可能是标签在每次轮询前选择时隙后空时隙或冲突时隙较多,算法不断调整时隙总数,导致命令数量增加.
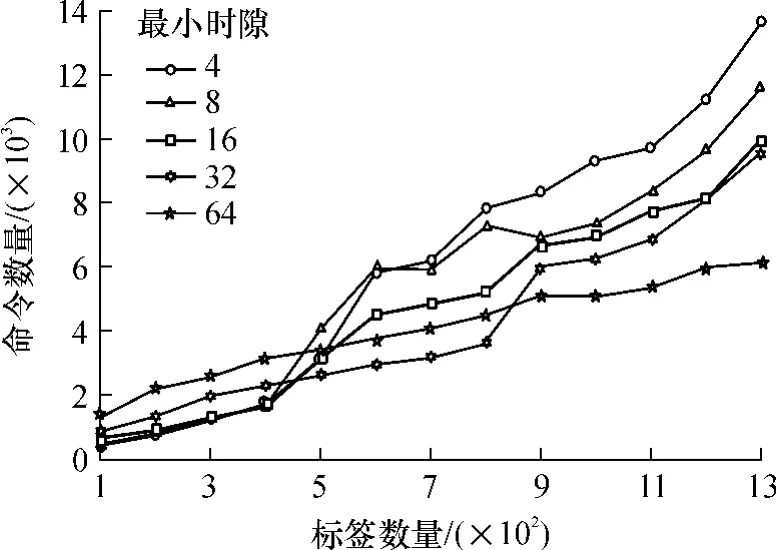
图3 不同最小时隙下文中算法的仿真结果比较Fig.3 Comparison of simulation results obtained by proposed algorithm with differentminimum slots
综上所述,当需要识别的标签较多时,可以增大最小时隙;当标签较少时,可以减小最小时隙以提高识别效率.
以相同的标签数据对二叉树算法和文中算法进行仿真,结果如图4所示.其中二叉树算法的实验结果是多次仿真结果的平均值;文中算法的结果是5种初始时隙实验中识别效率取得较好时的实验结果.从图4中可知,二叉树算法的识别速率随着标签数量的增加呈近似线性的上升,而在同样测试数据的前提下文中算法的识别速率比二叉树算法快.
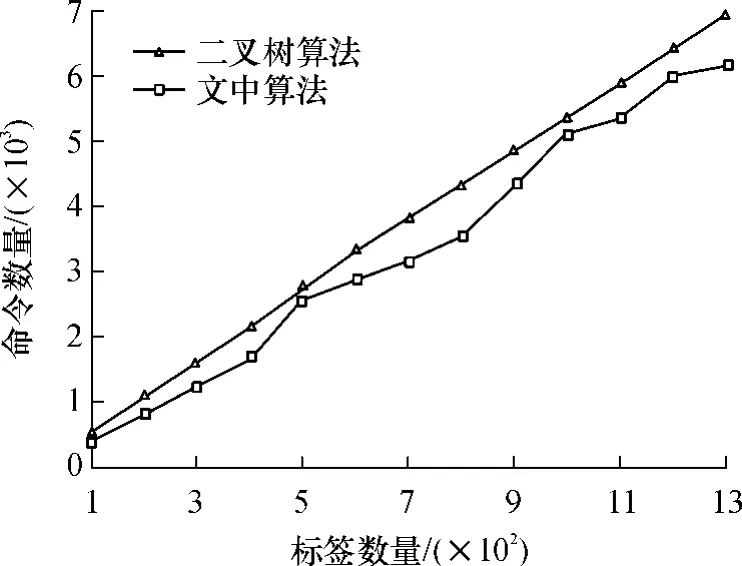
图4 二叉树算法与文中算法的仿真结果对比Fig.4 Comparison of simulation results between proposed algorithm and binary-tree algorithm
4 结语
文中提出了一种基于标签信息分组的射频识别防碰撞算法,将标签分成多个组,然后按组的顺序依次识别这些标签,以减少同一时刻响应阅读器请求的标签数量,从而降低碰撞发生的概率.算法中分组和时隙选择是最关键的两个因素,文中对这两个因素从理论上进行了证明,结果表明:标签能够相对均匀地分到各组中,从而保证了分组效率;标签在时隙选择上也相对分散,不会过度集中到其中一些时隙上;算法能够根据前一轮的轮询结果自适应地调整可选择时隙的范围.仿真实验结果表明:当标签总量较少、初始时隙范围较小时,算法性能较优,但随着标签数量的增加,初始时隙的范围越大越好;文中算法的性能要优于二叉树算法.从仿真结果看,文中算法具有一定的分组识别效率,但不是十分明显,从算法的结构看还有可以优化的空间,即轮询结束后,如果算法能更好地调整时隙选择范围,那么算法的分组识别效率会更优.今后将采用优化理论对算法进行优化,进一步分析文中算法的分组效率和识别性能,使其性能能够达到最优.
[1]Sarma S,Brock D,Engels D.Radio frequency identification and the electronic product code[J].IEEE Micro,2001,21(6):50-54.
[2]Jihoon Myung,Lee Wonjun.Adaptive binary splitting:a RFID tag collision arbitration protocol for tag identification[J].Communications Letters,2006,10(3):144-146.
[3]Waldrop J,Engels D,Sarma S.Colorwave:an anti-collision algorithm for the reader collision problem[C]∥Proceedings of IEEE International Conference on Communications.Anchorage:IEEE,2003:1206-1210.
[4]EPGglobal Inc.EPCTMradio-frequency identification protocols class-1 generation-2 UHF RFID protocol for communications at860MHz-960MHz Version 1.0.9[S].
[5]王铖岑.RFID系统防碰撞算法[J].计算机技术与发展,2010,20(1):29-32,35.Wang Cheng-cen.Anti-collision algorithm on RFID system[J].Computer Technology and Development,2010,20(1):29-32,35.
[6]Cha Jae-ryong,Kim Jae-hyun.Dynamic framed slotted ALOHA algorithms using fast tag estimation method for RFID system[C]∥Proceedings of IEEE Consumer Communications and Networking Conference.Las Vegas:IEEE,2006:768-772.
[7]江岸,伍继雄,黄生叶,等.改进的RFID二进制搜索防碰撞算法[J].计算机工程与应用,2009,45(5):229-235.Jiang An,Wu Ji-xiong,Huang Sheng-ye,et al.Improved RFID binary search anti-collision algorithm[J].Computer Engineering and Applications,2009,45(5):229-235.
[8]Hush Don R,Wood Cliff.Analysis of tree algorithms for RFID arbitration[C]∥Proceedings of IEEE International Symposium on Information Theory.Cambridge:IEEE,1998:107.
[9]Deng Huifang,Liu Jinqiao,Deng Chunhui,et al.RFID multi-tags anti-collision algorithm with adaptive Q leading to the maximum throughput[C]∥Proceedings of the Third Pacific-Asia Conference on Web Mining and Webbased Application.Guilin:IEEE,2010:166-169.
[10]万红,杨延昭.RFID防碰撞算法研究与改进[J].微计算机信息,2009,25(2/3):230-232.Wan Hong,Yang Yan-zhao.Research and improvement on anti-collision algorithm for RFID system[J].Microcomputer Information,2009,25(2/3):230-232.
[11]武强,李宏生,杨宇,等.UHF RFID系统防碰撞算法研究[J].仪表技术,2008(2):16-18,20.Wu Qiang,Li Hong-sheng,Yang Yu,et al.Research on anti-collision algorithm of UHF RFID system[J].Instrumentation Technology,2008(2):16-18,20.
[12]邓辉舫,刘金桥.RFID系统防碰撞中的二进制矩阵搜索[J].微计算机信息,2009,25(10-2):4-5,3.Deng Hui-fang,Liu Jin-qiao.Binary-matrix search in anticollision of RFID system[J].Micro-computer Information,2009,25(10-2):4-5,3.
[13]Wang Chun-yi,Lee Chi-chung.A grouping-based dynamic framed slotted ALOHA anti-collision method with fine groups in RFID systems[C]∥Proceedings of the 5th International Conference on Future Information Technology.Busan:IEEE,2010:1-5.
[14]ISO/IEC FDIS 18000-6,Information technology automatic identification and data capture techniques—radio frequency identification for item management air interface—part6:parameters for air interface communications at860-960MHz[S].
[15]Tanenbaurn A S.计算机网络[M].熊桂喜,王小虎,译.3版.北京:清华大学出版社,1997:137-142.
[16]Rotenberg A.A new pseudo-random number generator[J].Journal of the ACM,1960,7(1):75-77.
[17]Covyou R R.Serial correlation in the generation of pseudo-random numbers[J].Journal of the ACM,1960,7(1):72-74.
[18]Gereenberger M.Notes on a new pseudo-random number generator[J].Journal of the ACM,1961,8(2):163-167.
[19]ITU recommendation G.704,Synchronous frame structures used at primary and secondary hierarchical[S].

