考虑自由时差的资源均衡优化
马丹祥,初建宇,王海霞
(河北联合大学建筑工程学院;河北省地震工程研究中心,河北唐山,063009)
在网络计划中,“工期固定,资源均衡”优化是进行资源优化中的一类重要问题,在保持工期不变的条件下,可使资源需要量尽可能分布均衡,从而降低施工管理费与工程造价。解决此类问题的方法很多:在消高峰法的基础上刘在今等[1]提出了改进削高峰法,姚玉玲等[2]引入了“非关键工序组”的概念来减少优化工作量;骆刚等[3]采用遗传算法,张凯等[4]用粒子群算法分别对资源需求量方差最小模型求解。
资源均衡优化的基本原理就是通过调整工序的开工完工时间,以减少部分工序的时差为代价换取资源优化分配。由于工序时差的利用,增加了工序按期完工的风险,可能会影响紧后工序的执行甚至是总工期。现有对资源均衡的优化模型只是以资源均衡(资源均方差最小)为目标,而忽略了工序时差的减小带来的风险。因此,本文设计了资源分布方差尽量最小而网络计划中各工序自由时差和尽量最大的目标规划模型,这样该模型更具有实用性。
1 模型的建立
本目标规划模型共两个目标,第一优先级目标是单位时间资源需要量的均方差尽量最小,第二优先级的目标就是网络计划中各工序自由时差和尽量最大。工序的时差分总时差和自由时差两种,总时差是在不影响总工期的情况下该工作拥有的时差,自由时差是在不影响后续工作的情况下拥有的时差。由于工序的自由时差能更好的体现其对后续工序的影响,路线的自由时差(任意路线上所有工序的自由时差之和)能够反映路线的机动时间[5],所以这里用网络计划中各工序自由时差之和来反映项目能否按计划完成的风险。
模型如下:


式(1)为达成函数,表示在满足单位时间资源需要量的均方差尽量最小的前提下,网络计划中各工序自由时差之和尽量最大;式(2)为第一个目标约束,单位时间资源需要量均方差目标约束;式(3)为第二个目标约束,网络计划中各工序自由时差之和目标约束;通过式(4)、(5)可以求得t时刻所有工序资源的需求量;式(6)反映了每道工序之间的逻辑关系约束和时间关系约束,此约束可以剔除了无效数据,加快了优化进程;式(7)为人为限定的各工序自由时差之和的最小值,这样可以使模型有更大的适用空间;式(8)可以求得工序的自由时差;式(9)为非负约束。
2 粒子群算法基本原理与模型求解
2.1 粒子群算法基本原理
粒子群算法(POS)是由Eberhart和Kennedy于1995年提出的一种仿生智能优化算法,该算法是对鸟群觅食行为的模拟,是一种随机搜索算法。其将优化问题的一个解看做是搜索空间中的一个没有体积没有质量的粒子,在搜索空间中以一定的速度飞行,并根据对个体和集体的飞行经验的综合分析来动态调整这个速度。
标准POS中,粒子在搜索空间的速度和位置根据如下公式确定:
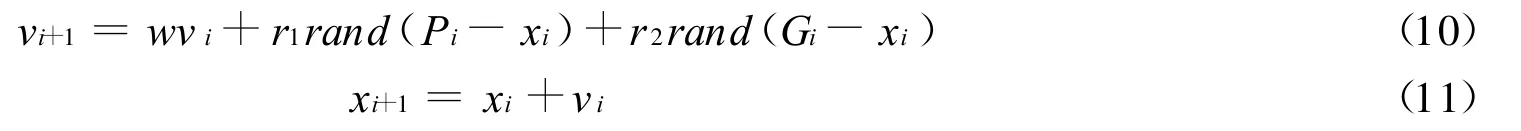
式中:w为惯性权重,r1、r2为加速常数,rand为区间[0,1]上均匀分布的随机数,Pi和Gi分别为i时刻粒子的自身最好位置pbest和全局最好位置gbest。Pbest为粒子自身飞过的最好位置,而gbest为粒子所对应的全局最好位置,它是整个群体所经历的最好位置。xi=(xi1,xi2,…,xin)与vi=(vi1,vi2,…,vin)为时刻i的位置与速度,为了避免跳过比较好的解,可以给飞行速度限定上限V max和下限V m in。
粒子群算法编码技术相对简单,容易实现并且没有许多参数需要调整,收敛速度快,相对于遗传算法等更简单有效,对于模型复杂、变量多、解空间维数大的优化问题具有很好的并行搜索能力,能较快的找到最优解。
2.2 模型求解的粒子群算法
该模型为目标规划,每个粒子的适应度值包括两部分:资源均方差尽量小为第一优先级目标,即使极小化;各工序自由时差之和尽量大为第二优先级目标,即使2极小化。因此在根据适应度值来确定粒子的自身最好位置pbest时和全局最好位置gbest时,值越小位置越好,如果值相同,就比较值,其值越小位置越好。
1)输入网络计划数据,初始化粒子群。在各工序的最早开工时间与最迟开工时间间,随机产生所有粒子的初始位置,并且要符合(6)与(7)的约束,满足自由时差和约束、工序的逻辑关系约束与时间关系约束;随机产生个粒子的速度,要满足速度的上下限;根据(1)~(5)计算适应度值,确定粒子的pbest(初始位置)和 gbest。
2)按照式(10)、(11)更新粒子的速度和位置,粒子的速度应在[V min,V max]内,如果超出取超出侧限值。由于此问题的决策变量为正整数,更新后粒子速度中有分量为小数,这里可以做四舍五入处理。更新后的粒子位置还要进行修正以符合(6)、(7)约束,如果粒子位置中分量超出约束(6)取超出侧限值,如不符合约束(7),则重新更新粒子的速度与位置,直至符合约束(7)。
4)根据(1)~(5)计算适应度值,按上述所述方法更新粒子的pbest和gbest。
5)如未达到结束条件(通常为预设的运算精度或迭代次数),返回步骤2)。
6)迭代结束取当前gbest为最优解。
3 实例应用及分析

图1 单代号网络图
图1为一个典型的单代号网络图,总工期14天,共9个工序,图中有一个虚拟开始活动和一个虚拟结束活动。工序的初始数据如表1,时间单位为天。初始网络计划资源均方差为24.4082。
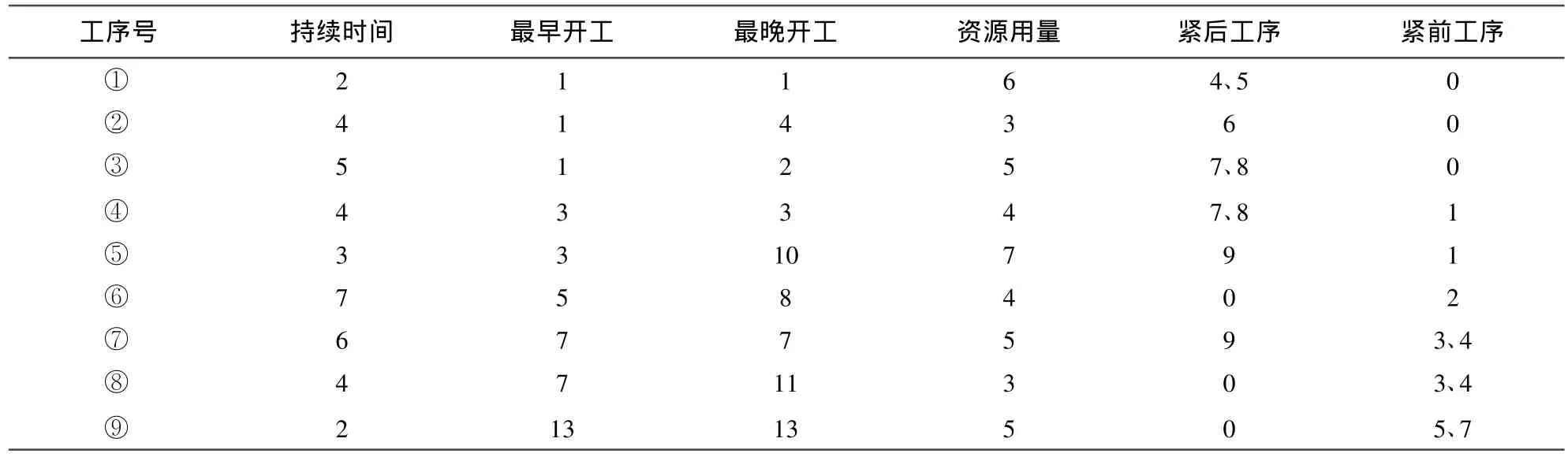
表1 各工序初始数据
当r1>r2且r1+r2<4.0时,算法能取得较好的优化效果[6][7],这里加速度系数r1取1.5,加速度系数r2取1.0,惯性权重w取1.0,速度限制为[-2,2],粒子规模取10,当全局最好位置连续10次不在更新迭代结束,利用MA TLAB编程,通过多次运行程序,针对该实例最多迭代16次即可得到最优解。
本实例在只考虑“工期固定——资源均衡”单一目标的情况下,可以得到资源均方差最小为2.836 7,共6种进度计划,在这6种进度计划中可能有些计划由于损失工序的机动时间大而增加了项目按计划执行的风险,为规避这种风险只能人工在这6种计划中挑选比较满意的进度计划,这样就比较复杂繁琐,为进度计划确定带来不便。
通过本文所建的模型就可以解决此问题。这里先把约束条件(7)中的F设定为0,及求项目资源尽量均衡情况下,网络自由时差之和尽量大的网络计划。通过计算可以得到如表2的进度计划数据,其中资源均方差仍然是2.836 7,但网络计划中各工序的自由时差之和为9,是资源均方差为2.836 7中自由时差和最大的方案。

表2 进度计划数据1
实际由于一些原因,可能要求网络计划中时差相对大些,以减少不能按期完成的风险,如第一次承接该类项目,各工序施工比较困难。这时就可以人为设定F的值,而达到降低风险的效果。针对该实例,F设定不同的取值进度计划数据如表3。

表3 进度计划数据2
根据表3中的数据,可以绘制F与资源均方差之间的趋势图,如图2,从图中可以看出随着F取值减小(允许损失机动时间越多),资源均方差越小,但机动时间损失到一定程度,最小资源均方差不再变化,说明并不是机动时间损失越多,资源越均衡。
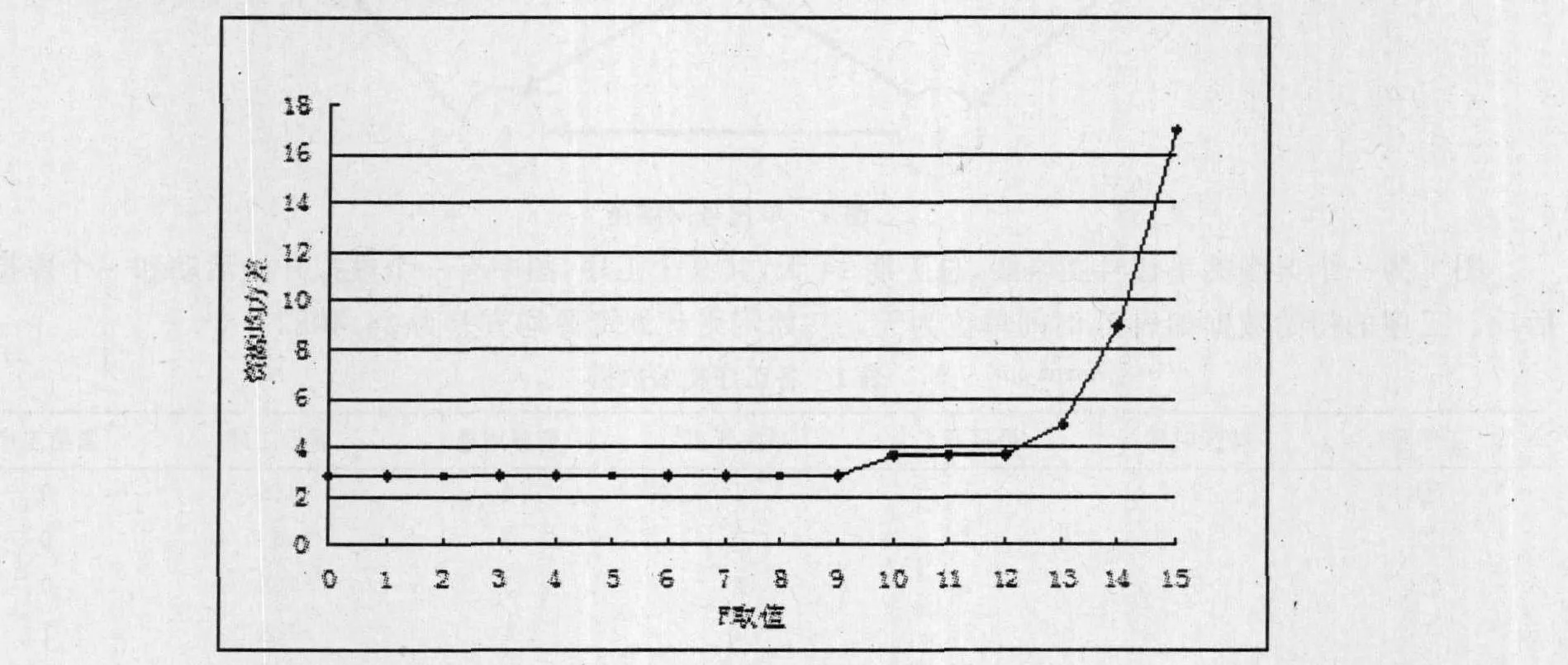
图2 趋势分析
4 结论及展望
针对现有对资源均衡的优化模型只是以资源均衡为目标,忽略了工序时差的损失而增大了风险的缺陷。本文设计了资源分布方差尽量最小而网络计划中各工序自由时差和尽量最大的目标规划模型,求得的进度计划较之前的单目标更具有实用性,并通过粒子群算法给出了求解途径。通过实例验证了模型与求解算法的有效性,并针对实例分析了自由时差损失与资源均方差之间的变化关系。本文采用各工序自由时差之和来衡量项目的执行风险,还不太确切,由于各工序的施工特性(难易程度和推迟的不确定性)并不完全相同,需要进一步研究考虑工序施工特性情况下的资源均衡问题。
[1] 刘在今,杜晓玲.改进削高峰法在网络计划优化中的应用[J].四川建筑科学研究,2007,33(1):197~199.
[2] 姚玉玲,贺晋荣.基于非关键工序组的资源均衡优化方法[J].长安大学学报(自然科学版),2005,25(1):101~104.
[3] 骆刚,刘尔烈,王健.遗传算法在网络计划资源优化中的应用[J].天津大学学报,2004,37(2):179~183.
[4] 张凯,赵国荣.粒子群优化算法在网络计划资源优化中的应用[J].海军航空工程学院学报,2008,23(1):75~78.
[5] 苏志雄,张立辉,李星梅.CPM网络计划中工序机动时间守恒性探究[J].运筹与管理,2009,18(4):144~151.
[6] SH IY H,EBERHART R C.A m odified Particle Sw arm Optim izer[C].International Conference on Evolutionary Computation,Anchorage,A laska,1998:69~73.
[7] SH IY H,EBERHART RC.Parameter selection in Particle Swarm Op timization[C].Annual Conference on Evolutionary Programm ing,SanDiego,1998.
[8] 李星梅,乞建勋,苏志雄.基于时差分析的资源均衡问题探究[J].中国管理科学,2007,15(1):47~54.
[9] 刘永建,赵胜利等.基于遗传算法的网络计划资源优化研究[J].河北农业大学学报,2007,30(5):115~118.
[10] 周宜红,李红亮等.改进微粒群算法在“资源一工期”优化中的应用[J].人民长江,39(11):64~66.

