OFDM系统时间同步方法性能比较

戈勇华,罗仁泽,,党煜蒲,易 丹

(1.重庆邮电大学光纤通信重点实验室光互联网研究所,重庆 400065;2.西南石油大学,成都 610500)

1 引 言

正交频分复用(OFDM)是一种多载波调制方式,其最大的优点是抗频率选择性衰落的能力强、频谱利用率高,已经应用在许多通信领域中[1],如数字地面广播电视(DVB-T)、数字音频广播(DAB)、无线局域网(WALN)等。

在高速移动环境下,由于传输信道的多径时延导致了定时偏移;同时,由于发射机和接收机两端振荡器的不稳定性和多普勒效应导致了载波频偏。因此,需要进行时间同步和频率同步,以良好的定时来确定OFDM帧的起始位置,保信号的正确解调。

本文对具有代表性的算法进行分析和仿真比较,指出其存在的不足之处,同时给出了提高时间同步性能的几点建议。

2 同步算法

现有的同步技术主要是通过序列的相关性来获取同步信息,一个良好相关性的序列可以获取较高的系统时间准确率。根据同步算法所利用的数据及方式不同,可以大致分为4类:基于循环前缀的同步算法、插入训练序列同步算法、插入导频时间同步算法和叠加训练序列时间同步算法。

2.1 基于循环前缀的同步算法

为了有效对抗符号间干扰(ISI)和信道干扰(ICI),将OFDM符号后面的部分插入到该符号的前面,构成循环前缀(CP)。在接收端,观察相隔一个符号长度为N的两个接收符号间的相关性一般采用延时相关的算法[2]。

文献[3-10]的改进算法通过多个循环前缀的信息获得更优的同步性能,其中文献[3,5,7,8]采用最大似然(ML)算法,通过引入信噪比和加权因子的方式来减小 ISI的影响,改善了算法的性能;文献[4]通过减小采样时钟频率偏移的敏感性,利用大的运算量和复杂度来换取高的同步性能;文献[10]通过融合循环前缀信息和PN序列的相关来改善时间同步性能,但是算法所获得性能仍不理想。

该算法的优点:利用循环前缀包含的信息进行相关运算而获取同步,不需要其它训练序列,可以在失步后,很快建立同步。但由于OFDM系统特有的抗多径信道干扰能力,此类方法在多径信道下,系统的同步性能不会下降很多。利用检测相关峰值法时,受到定时点附近的峰值点影响比较大,对检测干扰很大,影响了系统的同步性能;同时,此类方法使用的是循环前缀中不受ISI影响的区域来寻找最大的时间频率估计,但这种不受影响的区域在实际应用过程中很难准确地识别出来,这将影响系统的同步性能。

2.2 插入训练序列同步算法

基于训练序列的OFDM系统同步方法其基本思想是:在发射端,将训练序列插入一个完整OFDM数据符号前或者是由多个OFDM数据符号构成的帧前;而在接收端,利用插入训练序列良好的自相关性来进行定时信息的提取及频偏估计等。

文献[11]提出PN序列进行同步,利用两个相同的OFDM训练模块插入分组或帧的头部,利用相同结构之间的时域相关性来进行频偏的估计。这种估计的同步精度高,但捕获范围小;若增大捕获范围,同步精度将会降低。文献[12]利用两个训练符号来完成时间频率同步。采用的是第一个训练符号由前后完全相同的两部分序列组成,利用这两部分的相关性,通过寻找其相关的最大值来完成符号同步。该方法有很强的时频偏估计能力,计算复杂度不高。但是,在信噪比较高的情况下,该方法的相关峰值出现一个较宽的峰值平台,影响了同步的准确率。

文献[13]对Schmidl训练符号的结构进行了改进,将训练符号列分成4部分,改进后的目标函数比较尖锐,提高了符号定时的准确度。文献[14]引入了序列的共轭对称特性,对序列进行重新构造,改进后的定时度量函数具有单一的峰值,大大提高了定时准确度,但Park算法在信噪比较低的情况下峰值不明显,旁瓣比较多,影响了系统的同步性能。

文献[15]提出利用重复PN序列的OFDM时间频率同步算法,主要是将长度为N的序列按照PN序列的长度分成若干份,在接收端,利用PN序列良好的自相关性来提取同步信息。该算法具有时间同步准确率高、频率同步估计范围和精度可调节等性能。

文献[11-19]中的时间同步算法均在时域内进行,同步算法主要依据构造训练序列的不同来实现的。构造一个具有较好的优良相关性的新序列进行同步算法是提高系统同步准确的关键,特别是引进序列的共轭对称结构可以大大增加系统的同步性能。但是,此类算法存在缺陷,在频率资源有限的情况下,插入的训练序列占用频带资源,从而降低了频谱的利用率;同时,所插入的训练序列独占发射功率,在一定程度上降低了发射机的效率。还有,在信噪比较低的情况下,该类方法的同步准确率较低。

2.3 插入导频时间同步算法

传统采用导频同步主要是在频域内插入导频,利用事先插入的导频符号在频域内的相关性,遵循ML估计准则。

文献[20]基于连续导频,利用导频之间的相关性获取同步,在DVB-T系统中获得了较好的性能。文献[21]通过在频域插入离散导频符号,并将帧设计为具有共轭性结构,使得系统同步性能得到改善。

实质上,利用频域插入导频获取同步性能与导频的设计密切相关,应用于欧洲的DVB-T系统中。但这些导频占用了宝贵的频带资源,因此在其它系统中的使用将受到限制。同时,在高速移动环境下DVB-T系统的同步性能改进仍然是学术界研究的难点。

2.4 叠加训练序列时间同步算法

叠加训练序列时间同步算法主要是与插入训练序列时间同步算法进行区分。叠加训练序列的思想起源于 1965年[22]。将叠加训练序列最早用于OFDM系统中同步的是文献[23]。后来,文献[24]基于叠加训练序列提出了同步算法。其主要思想是:在发射端,将训练序列乘以相应的功率分配因子后在一个符号周期内与数据同时发送;在接收端,利用本地序列与接收信号进行相关运算,对所叠加训练序列进行能量累积来实现时间同步。

文献[24]针对叠加PN序列的OFDM系统提出了一种时间频率同步算法,将训练序列c(n)乘以功率分配因子 β后再加到用户数据上,为了保持总能量不变,将用户数据乘以功率分配结构图如图1所示。

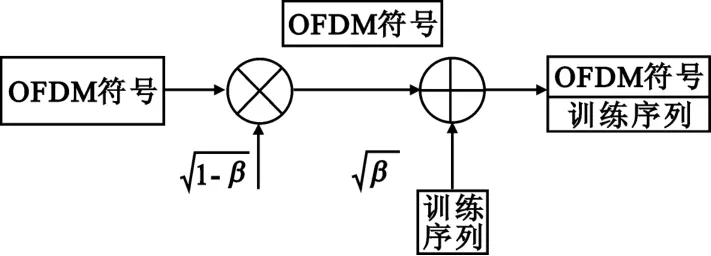
图1 叠加训练序列结构示意图Fig.1 Structure of superimposed training sequence

文献[25]提出了一种叠加训练序列的同步算法,采用最大似然法(ML)准则进行时间、频率估计,获得了较好的同步性能,但该算法中采用了信道的信噪比,在实际的应用中,信道的信噪比难以确定,这将影响算法的实际应用。文献[26]提出了两种不同的重复周期且具有良好自相关性的m序列分别叠加在用户的偶数和奇数帧的帧同步算法,通过接收信号与本地m序列进行相关来获取同步,算法性能较好,但该算法使用时叠加了两个用户帧,这将降低发射机的功效,同时影响系统的误码率性能。

虽然采用叠加训练序列来实现同步能够获得较好的同步性能,但也存在一个非常关键的技术问题。由于训练序列叠加在OFDM用户数据上,对数据产生影响并导致系统的误码性能下降。因此,必须在接收端提出相应的消除机制来减小训练序列对系统误码性能的影响。

3 同步算法比较分析

仿真参数设置:OFDM系统子载波数 Nc=256,CP的长度Ncp=N/4,调制方式为4-QAM,多径信道数 L=6。

从图2中可以看出,每个峰值代表的是接收信号延时N点后的相关值,即循环前缀相关运算后所累积的能量值,一旦失步后,可以利用其它峰值来重新建立同步。

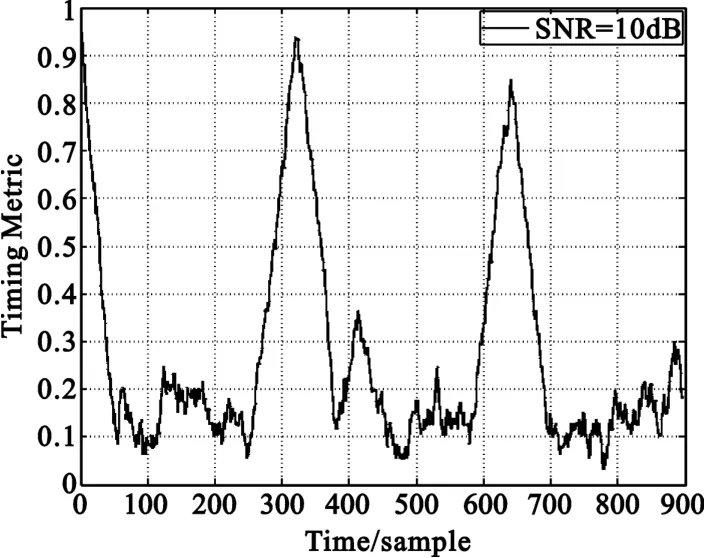
图2 利用循环前缀的同步算法相关峰值Fig.2 Correlation peak of synchronization algorithms by using cyclic prefix

从图3中可以看出,Schmidl时间同步算法随着信噪比的增加,出现了峰值平台,且峰值不尖锐,这将给同步的判断带来模糊性。

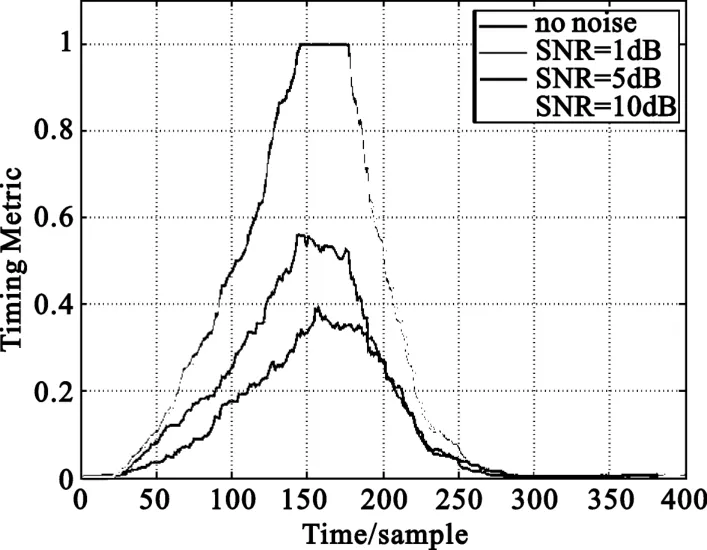
图3 Schmidl时间同步算法相关峰值Fig.3 Schmidl′s timing metric correlation peak

从图4可以看出,H.Minn时间同步算法比Schmidl时间同步算法有所改进,出现了比较尖锐的峰值,但这种算法的模糊性比较大,且同步准确率不高。

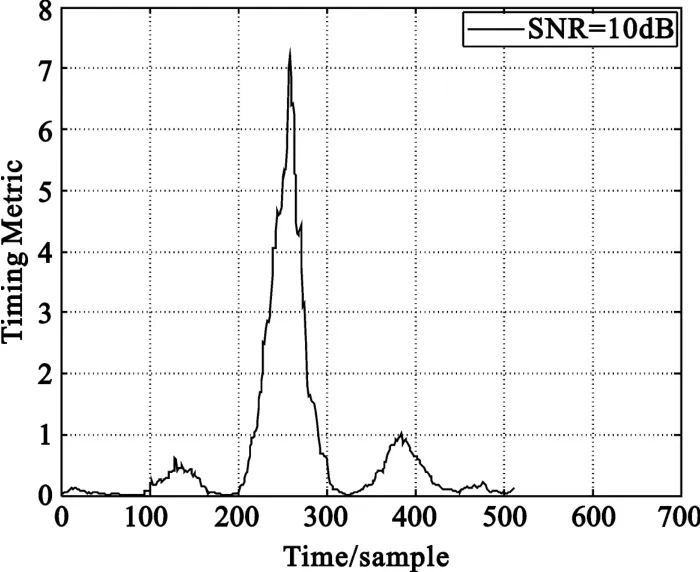
图4 H.Minn时间同步算法相关峰值Fig.4 H.Minn′s timing metric correlation peak

Park时间同步算法是在H.Minn的训练结构中引进共轭对称结构,从图5中可以看出,该算法具有单一的峰值性,利用时间同步判断,同步准确率比较高,但这种算法旁瓣比较多,特别是利用设定门限值来判断的时候,可能给同步判断带来影响。

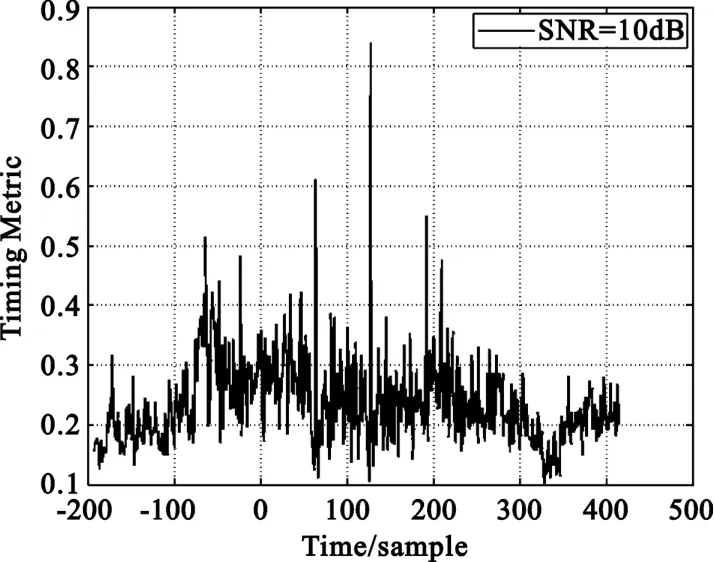
图5 Park时间同步算法相关峰值(多径信道)Fig.5 Park′s timing metric correlation peak(multi-channel)

从图6中可以看出,叠加训练序列时间同步算法具有较好的单一峰值性,且旁瓣比较少,这将给同步判断带来很大的有利条件。

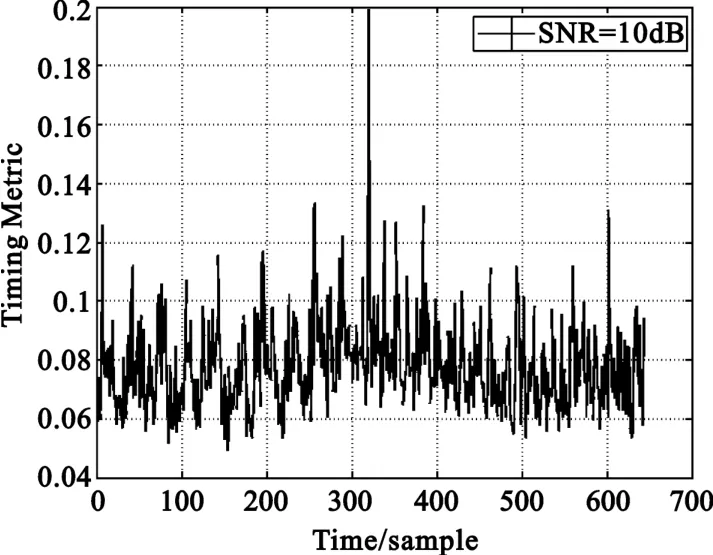
图6 叠加训练序列时间同步算法相关峰值(多径信道)Fig.6 Superimposed training timing metriccorrelation peak(multi-channel)

图7为高斯信道下不同时间同步算法在相同的信噪比下的同步正确率对比。从图7中可以看出,在相同信噪比下,叠加训练序列具有较好的同步正确率。基于循环前缀的时间同步算法其同步性能较差,主要是相关峰值无法达到像Park和叠加训练序列同步算法单一的尖峰值。Schmidl时间同步算法与其它的同步算法相比,性能最差,主要是峰值平台给估计同步带来模糊性。

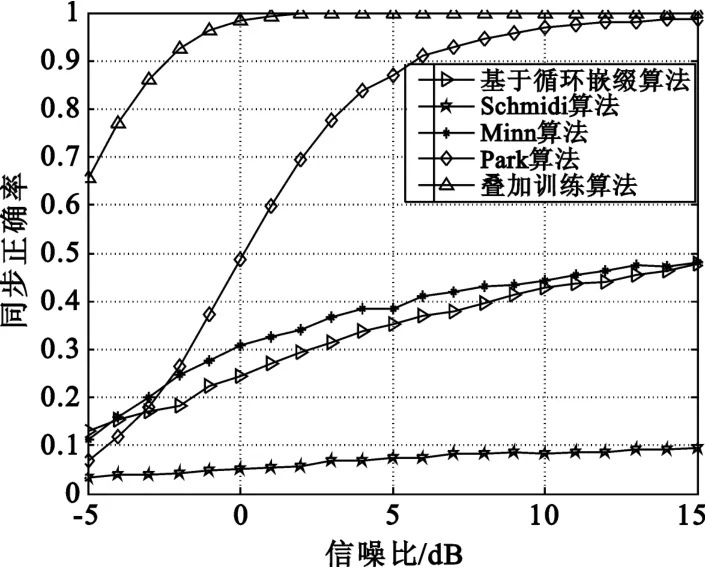
图7 不同时间同步算法性能对比Fig.7 Performance comparison among different timing algorithms

4 时间同步算法研究与展望

目前,对OFDM无线通信系统的时间同步算法研究已经取得了很大的进展,但现有的时间同步算法还有待提高,本文认为可以从以下几个方面进行进一步的研究。

(1)由于OFDM无线通信系统的时间同步算法都采用序列的相关性来取得同步信息,当达到同步时刻,相关性最强,峰值最大,因此,寻找具有较好相关性能的序列,可以提高同步的准确度。近几年来,由于CAZAC序列具有恒包络和自相关函数为零的良好性质,可以减小放大器非线性的影响,提高OFDM系统同步和信道估计的性能,因而基于CAZAC序列的训练符号设计和同步算法得到了广泛的研究。

(2)通过H.Minn对Schmidl序列结构改进及经典Park算法的提出可以得到启示,通过改变训练序列及引进共轭对称性,重新构造新的序列结构,可以提高系统的同步精度。

(3)由于无线频谱资源的有限,采用叠加训练序列的同步方法可以解决插入训练序列占用频带的缺陷,且不独占发射机的所有发射平均功率,因此,提高了系统的传输效率,这为以后的学者提供了有效的研究方向,但同时应想办法解决叠加训练序列对用户数据的影响。

(4)目前,大多学者都忽略了循环前缀含有丰富的信息,通过充分利用循环前缀的信息,联合其它同步算法,可以增加定时符号算法峰值,有效提高系统的同步性能,一旦失步后,还可以利用循环前缀来建立同步。

(5)性能评价模型。现有OFDM无线通信系统时间同步算法之间的性能对比都是通过相同运行环境下的实验进行,因此建立一个标准的性能评价模型也是一个值得研究的方向。

总之,本文通过对现有的时间同步算法进行了分类,给出了经典时间同步算法的仿真图,为广大学者提供了进一步改进同步准确率的方向。OFDM无线通信系统时间同步是一个研究热点领域,其中还有许多问题亟待解决,值得我们的关注和进一步研究。

[1] 方向红.OFDM通信系统的符号和频率同步算法研究[D].南京:南京大学,2006.FANG Xiang-hong.OFD M Communication System Sympol and Frequency Synchronization[D].Nanjing:Nanjing University,2006.(in Chinese)

[2] CHEN Li.Three Symbol Synchronization Algorithms Basedon PN Sequence for OFD M Systems[J].Journal of Chongqing Institute of Technology(Natural Science),2009,23(1):113-116.

[3] J-J-Vande Beek,M Sandell.ML estimation of timing and frequency offset in multicarrier systems[J].IEEE Transactions on Signal Processing,1997,45:1800-1804.

[4] Zhang Rong-tao,Xie Xian-zhong,Wang Xi.A Synchronization Algorithm for OFDM based on Training Cyclic Prefix[J].T ransactions on Communications,2007,51(3):1122-1125.

[5] Hamza A M,Sourour E,El-Khamy S.Low complexity novel methods for initial timing synchronization in mobile WiMAX OFD MA system[C]//Proceedings of 2010 IEEE 72nd Vehicular Technology Conference Fall.Ottawa,ON:IEEE,2010:1-5.

[6] 常山民.一种改进的基于循环前缀的OFDM系统定时同步方法[J].中国西部科技,2008,28(7):1-3.CHANG Shan-min.A modified timing synchronication method based on cyclic prefix in OFDM systems[J].West China Technology,2008,28(7):1-3.(in Chinese)

[7] Takahashi K,Saba T.A novel symbol synchronization algorithm with reduced influence of ISI for OFDM systems[C]//Proceedings of Global Telecommunications Conference.San Antonio,Texas,USA:IEEE,2001:524-528.

[8] Ramasubramanian K,Baum K.An OFD M timing recovery scheme with inherent delay-spread estimation[C]//Proceedings of Global Telecommunications Conference.San Antonio,Texas,USA:IEEE,2001:3111-3115.

[9] Landstrom D,WilsonS K,Beek J J van de,et al.Symbol time offset estimation in coherent OFDM systems[J].IEEE Transactions on Communications,2002,50(4):545-549.

[10] GUO Da,JIANG Feng,SONG Mei,et al.A novel symbol synchronization scheme using multiple symbols in OFDM systems[J].Journal of Circuits and Systems,2007,12(3):94-97.

[11] Moose P.A technique for OFDM frequency offset correction[J].IEEE Transactions on Communications,1994,42(10):2908-2914.

[12] Timothy M Schmidl,Donald C Cox.Robust Frequency and Timing Synchronization for OFDM[J].IEEE Transactions on Communications,1997,45(12):1613-1621.

[13] Minn H,Zeng M,Bhargava V K.On timing offset estimation for OFDM systems[J].IEEE Communications Letters,2000,4(7):242-244.

[14] Park B,Cheon H,Kang C,et al.A novel timing estimation method for OFDM systems[J].IEEE Communication Letters,2003,7(5):239-241.

[15] Tufvesson F,Faulkner M,Edfors O.Time and frequency synchronization for OFDM using PN-sequence preambles[C]//Proceedings of IEEE Vehicular Technology Conference.Amsterdam:IEEE,1999:2203-2207.

[16] Guangliang Ren,Yilin Chang,Hui Zhang,et al.Synchronization Method Based on a New Constant Envelop Preamble for OFDM Systems[J].IEEE Transactions on Broadcasting,2005,51(1):139-143.

[17] Ma Yangjun,Hu Yaonu.An improved training sequence based OFDM synchronization algorithm[J].Study onOptical Communications,2009,35(6):65-67.

[18] Zongshan Pang,Xiaomin Li.A Novel Synchronization Algorithm for OFDM System Based on Training Sequence Added Scramble Code[C]//Proceedings of IEEE International Conference on Communications Technology and Applications.Beijing:IEEE,2009:527-531.

[19] Shun-Sheng Wang,Chih-Peng Li,Chin-Liang Wang.A Novel Timing and Frequency Offset Estimation Scheme for OFDM Systems[J].IEEE Transactions on Signal Processing,2007,48(3):1713-1717.

[20] Eun SuKang,Humor Hwang,Dong Seog Han.A fine carrier recovery algorithm robustto Doppler shift for OFDM systems[J].IEEE Transactions on Consumer Electronics,2010,56(3):1218-1222.

[21] Kocan E,Pejanovic-Djurisic M,Veljovic Z.Efficient frequency synchronization and channel estimation method for OFDM wireless systems[C]//Proceedings of the 15th IEEE Mediterranean Electrotechnical Conference.Valletta:IEEE,2010:487-491.

[22] Kastenholz C E,Birkemeier W P.A simulation information transfer and channel sounding modulation technique for wide-band channels[J].IEEE Transactions on Communication Technology,2004,56(4):162-165.

[23] Steinga B A,Van Wijingaarden A J,Teich W G,et a1.Frame synchronization using superimposed sequence[C]//Proceedings of 1997 International Symposium on Information Theory.Ulm,Germany:IEEE,1997:489.

[24] Tufvesson F,Edfors O,Faulkner M.Time and frequency synchronization for OFD M using PN-sequence preambles[C]//Processing of the 50th IEEE Vehicular T echnology Conference.Amsterdam,Netherlands:IEEE,1999:2203-2207.

[25] Chih-Peng Li,Wei-Wen Hu.Super-Imposed Training Scheme for Timing and Frequency Synchronization in OFDM Systems[J].IEEE Transactions on Broadcasting,2007,53(2):574-583.

[26] Guoqiang Gong,Wancheng Ge.An Equalization Method for TDS-OFDM Systems over Fast Fading Channels[C]//Proceedings of 2009 International Conference on Networks Security,Wireless Communications and Trusted Computing.Wuhan,Hubei:IEEE,2009:133-136.